№5: ОТОБРАЖЕНИЯ МНОЖЕСТВ. ИНЪЕКТИВНЫЕ, СЮРЪЕКТИВНЫЕ И БИЕКТИВНЫЕ ОТОБРАЖЕНИЯ. ПРИМЕР

Отображения множеств

Пусть U, V - непустые множества, - (однозначное) отображение из множества U в множество V, т. е. каждому элементу сопоставляется элемент .

Замечание

1. Сохраняя единообразие с курсом анализа, мы обозначаем применение отображения f к элементу через f(u), т. е. f пишем слева от u. Возможно (а иногда и удобнее) было бы использовать обозначение uf.

2. Если , то f=f', если для любого имеем f(u)=f'(u).

3. Категория Set, в которой объекты - множества, морфизмы - отображения множеств, является одной из основных категорий в математике.

Инъективные, сюръективные, биективные отображения

Рассмотрим образ отображения

Можно рассмотреть также полезное отношение эквивалентности на множестве U, определяемое отображением ,

Определение .Отображение называется:

1. инъективным, если разные элементы в U при отображении f переходят в разные элементы в V (т. е. ),

2. сюръективным, если каждый элемент в V является образом некоторого элемента из U (т. е. , другими словами, ),

3. биективным, если отображение f инъективно и сюръективно (т. е. ).

Замечание

1. В более ранней математической литературе для биективного отображения использовалась более длинная комбинация слов: "взаимно однозначное отображение на",

2. иногда для сюръективного отображения мы будем говорить, что " f отображает множество U на множество V ".

Задачи

1. Пусть |U|=m, |V|=n. Доказать, что .

2. Пусть |U|=m, L(U) - совокупность всех подмножеств множества U (включая пустое подмножество). Доказать, что |L(U)|=2^m.Указание.

Для подмножества рассмотреть его характеристическую функцию 

Следствие

 .


3. Найти число инъективных (сюръективных) отображений , где |U|=m, |V|=n.

Пример .

1. Отображение f: N -> N, f(n)=n+1, является инъективным, но не является сюръективным.

2. Отображение f: N -> N, f(1)=1 и f(n)=n-1 для n>1, является сюръективным, но не является инъективным.

3. Тождественное отображение 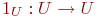, 1_U(u)=u для всех , очевидно, является биекцией.

Лемма. Пусть U - конечное множество, . Тогда равносильны условия:

1. f - инъективное отображение;

2. f - сюръективное отображение.

Доказательство.

Пусть . Так как - инъективное отображение, то . Поскольку , , то , т. е. f - сюръективное отображение.

Допустим противное, т. е. что не является инъективным отображением. Тогда для некоторых , . Следовательно, |Im f|<n=|U|, поэтому Im f<U, т. е. отображение f не является сюръективным, что приводит к противоречию.

№6

Определение. Если для подмножества

Множество ограниченно сверху


Определение. Множество, не являющееся ограниченным сверху множеством, называется неограниченным сверху множеством.

Множество не ограниченно сверху .


Определение. Если для подмножества , то множество

Множество ограниченно снизу .


Определение. Множество, не являющееся ограниченным снизу множеством, называется неограниченным снизу множеством.

Множество не ограниченно снизу .


Определение. Множество, ограниченное и сверху и снизу, называется ограниченным множеством.

Определение. Множество, не являющееся ограниченным, называется не ограниченным множеством.


Определение. Наименьшее среди всех чисел, ограничивающих сверху множество , называется его верхней гранью и обозначается через


Определение. Наибольшее среди всех чисел, ограничивающих снизу множество , называется его нижней гранью и обозначается через


Пример. , где


Теорема. ограниченное сверху непустое числовое множество имеет верхнюю грань, а всякое ограниченное снизу непустое числовое множество имеет нижнюю грань.

Доказательство. Пусть

Выполнение неравенства означает, что число

-е верхней грани у ограниченного сверху непустого множества доказано.

Если теперь

Аналогично рассмотренному случаю верхней грани, легко убеждаемся, что, в силу свойства неперрывности действительных чисел, и имеет место неравенство .

Это означает, что

№9

нету достоверной информации!!!!

№10

Ограниченные и неограниченные последовательности

      Числовая последовательность {х_n} называется ограниченной, если существуют числа m и M, такие, что любой элемент x_n этой последовательности удовлетворяет неравенствам

m ≤ x_n ≤ M.

      Пусть А = max{ | m |, | M |}. Тогда условие ограниченности последовательности можно записать в виде | x_n | ≤ А n ≥ N:

   Здесь и в дальнейшем будем пользоваться квантором всеобщности и квантором существования . Не вдаваясь в подробности определения этих логических операций, будем читать квантором всеобщности как "для любого", а квантор существования как "существует".   Последовательность {х_n} называется неограниченной, если для любого как угодно большого положительного числа А существует элемент x_n этой последовательности, удовлетворяющий неравенству | x_n | > A, (т.е. либо x_n > A, либо x_n < - A):

  Последовательность ограничена сверху, если все ее элементы принадлежат промежутку ( - ∞, M]:

  Последовательность ограничена снизу, если все ее элементы принадлежат промежутку [m, + ∞):

   З а м е ч а н и е. Неограниченная последовательность может быть ограничена сверху (снизу).

  Сравнивая запись с помощью логических символов двух последних определений, видим, что при построении отрицаний символы и заменяют друг друга и неравенства меняют свой смысл.

№15

Бесконечно большие и бесконечно малые последовательности

   Определение. Последовательность { х_n} называется бесконечно большой, если для как угодно большого любого положительного числа А существует номер N, зависящий от этого числа А, такой, что для всех последующих номеров n > N выполняется неравенство | x_n | > A:

   Замечание. Очевидно, что любая бесконечно большая последовательность является неограниченной. Однако неограниченная последовательность может и не быть бесконечно большой. Например, неограниченная последовательность 1, 2, 1, 3, …, 1, n + 1, … не является бесконечно большой, поскольку при A > 1 неравенство | x_n| > A выполняется не для всех элементов x_n с нечетными номерами.

   Определение. Последовательность {α_n} называется бесконечно малой, если для любого как угодно малого положительного числа ε > 0 существует номер N, зависящий от этого ε, такой, что для любых n > N выполняется неравенство |α_n| < ε:

№16

Предел суммы или разности сходящихся последовательностей

  Сумма (разность) двух сходящихся последовательностей {x_n} и {y_n) есть сходящаяся последовательность, предел которой равен сумме (разности) пределов последовательностей {x_n} и {y_n).

 Д о к а з а т е л ь с т в о. Пусть a и b – соответственно пределы последовательностей {x_n} и {y_n}. Тогда по определению имеем

Абсолютная величина разности может быть как угодно малой при всех n > N, если выбрать N = max{N₁, N₂ }:

,

что и доказывает сходимость последовательности {x_n ± y_n} к a ± b.