Определение матрицы. Виды матриц.

Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины (или n столбцов одинаковой длины). Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются aij, где i - номер строки матрицы, а j - номер столбца матрицы. У матрицы есть 2 диагонали. Элементы, стоящие на диагонали, идущей из верхнего угла, образуют главную диагональ матрицы, а элементы стоящие на другой диагонали образуют вспомогательную диагональ матрицы.

Матрица записывается ввиде:

Матрицу А называют матрицей размера "m×n" и пишут Аm×n. Матрица может состоять как из одной строки, так и из одного столбца. Вообще говоря, матрица может состоять даже из одного элемента.

Матрицы равны между собой, если равны все соответствующие элементы этих матриц, т. е. А = В, если aij = bij. Матрица А называется симметричной, если она квадратная и если все aij= аji.

Если (m = n), то матрица называется квадратной. Квадратную матрицу размера "n×n" называют матрицей n - ого порядка. Квадратную матрицу, у которой все элементы, кроме элементов главной диагонали, равны нулю, называю диагональной матрицей. Диагональная матрица :

Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной матрицей. Обозначается буквой Е. Единичная матрица :

Квадратная матрица, называется треугольной, если все элементы матрицы, расположенные по одну сторону от главной диагонали, равны нулю. Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается буквой О. В матричном исчисленииматрицы О и Е играют роль 0 и 1 в арифметике. Матрица, содержащая одну строку или один столбец, называется вектором (Или вектор-строка, или вектор-столбец соответственно).

Матрицу В называют транспонированной матрицей А, а переход от А к В транспонированиемматрицы, если элементы каждой строки матрицы А записать в том же порядке в столбцыматрицы В. Обозначается АТ.

Другими словами, aij = bji.

Операции над матрицами: сложение, умножение матрицы на число, умножение матриц.

Вычитание и сложение матриц сводится к соответствующим операциям над их элементами.Операция сложения матриц вводится только для матриц одинакового размера, т. е. дляматриц, у которых число строк и столбцов соответственно равно. Суммой матриц А и В, называется матрица С, элементы которой равны сумме соответствующих элементов. С = А + В cij = aij + bij Аналогично определяется разность матриц.

Умножение матрицы на число:

Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число. Произведением матрицы А на число k называется матрица В, такая что bij = k × aij. В = k × A bij = k × aij. Матрица   - А = (-1) × А   называется противоположной матрице А.

Свойства сложения матриц и умножения матрицы на число:

Операции сложения матриц и умножения матрицы на число обладают следующими свойствами: 1. А + В = В + А; 2. А + (В + С) = (А + В) + С; 3. А + 0 = А; 4. А - А = 0; 5. 1 × А = А; 6. α × (А + В) = αА + αВ; 7. (α + β) × А = αА + βА; 8. α × (βА) = (αβ) × А; , где А, В и С - матрицы, α и β - числа.

3.Элементарные преобразования матриц

Элементарными преобразованиями матрицы называются следующие преобразования: 1) умножение строки матрицы на число, отличное от нуля; 2) прибавление к одной строке матрицы другой строки; 3) перестановка строк; 4) вычеркивание (удаление) одной из одинаковых строк (столбцов); 5) транспонирование матрицы;

Те же операции, применяемые для столбцов матрицы, также называются элементарными преобразованиями. С помощью элементарных преобразований можно к какой-либо строке или столбцу матрицы прибавить линейную комбинацию остальных строк (столбцов).

Умножение матриц (Произведение матриц):

Операция умножения двух матриц вводится только для случая, когда число столбцов первойматрицы равно числу строк второй матрицы. Произведением матрицы Аm×n на матрицу Вn×p, называется матрица Сm×p такая, что сik = ai1 × b1k + ai2 × b2k + ... + ain × bnk, т. е. находиться сумма произведений элементов i - ой строки матрицы А на соответствующие элементы j - ого столбца матрицы В. Если матрицы А и В квадратные одного размера, то произведения АВ и ВА всегда существуют. Легко показать, что А × Е = Е × А = А, где А квадратная матрица, Е - единичная матрица того же размера.

Свойства матриц:

Умножение матриц обладает следующими свойствами: 1. А × (В × С) = (А × В) × С; 2. А × (В + С) = АВ + АС; 3. (А + В) × С = АС + ВС; 4. α × (АВ) = (αА) × В; 5. А × 0 = 0; 0 × А = 0; 6. (АВ)Т = ВТАТ; 7. (АВС)Т = СТВТАТ; 8. (А + В)Т = АТ + ВТ

4. Перестановки, построение определителей n-го порядка. Свойства определителей.

Определители матриц, способ № 1:

Определителем квадратной матрицы (det A) называется число, которое может быть вычислено по элементам матрицы по формуле:

, где М1k - определитель матрицы (детерминант), полученной из исходной матрицывычеркиванием первой строки и k - oго столбца. Следует обратить внимание на то, чтоопределители имеют только квадратные матрицы, т.е. матрицы, у которых число строк равно числу столбцов. Первая формула позволяет вычислить определитель матрицы по первой строке, также справедлива формула вычисления определителя матрицы по первому столбцу:

Вообще говоря, определитель матрицы может вычисляться по любой строке или столбцуматрицы, т.е. справедлива формула:

Очевидно, что различные матрицы могут иметь одинаковые определители. Определитель единичной матрицы равен 1. Для указанной матрицы А число М1k называется дополнительным минором элемента матрицы a1k. Таким образом, можно заключить, что каждый элемент матрицы имеет свой дополнительный минор. Дополнительные миноры существуют только в квадратных матрицах.

Дополнительный минор произвольного элемента квадратной матрицы aij равенопределителю матрицы, полученной из исходной матрицы вычеркиванием i-ой строки и j-го столбца.

Замечание:

Вычисление определителей матриц четвертого и более высокого порядка приводит к большим вычислениям, так как:

для нахождения определителя матрицы первого порядка мы находим одно слагаемое, состоящее из одного сомножителя;

для нахождения определителя матрицы второго порядка нужно вычислить алгебраическую сумму из двух слагаемых, где каждое слагаемое состоит из произведения двух сомножителей;

для нахождения определителя матрицы третьего порядка нужно вычислить алгебраическую сумму из шести слагаемых, где каждое слагаемое состоит из произведения трех сомножителей;

для нахождения определителя матрицы четвертого порядка нужно вычислить алгебраическую сумму из двадцати четырех слагаемых, где каждое слагаемое состоит из произведения четырех сомножителей и т.д.

Определить количество слагаемых, для нахождения определителя матрицы, в алгебраической сумме, можно вычислив факториал: 1! = 1 2! = 1 × 2 = 2 3! = 1 × 2 × 3 = 6 4! = 1 × 2 × 3 × 4 = 24 5! = 1 × 2 × 3 × 4 × 5 = 120 ...

Свойства определителей матриц:

Свойство № 1:

Определитель матрицы не изменится, если его строки заменить столбцами, причем каждую строку столбцом с тем же номером, и наоборот (Транспонирование). |А| = |А|Т

Следствие:

Столбцы и строки определителя матрицы равноправны, следовательно, свойства присущие строкам выполняются и для столбцов.

Свойство № 2:

При перестановке 2-х строк или столбцов определитель матрицы изменит знак на противоположный, сохраняя абсолютную величину, т.е.:

Свойство № 3:

Определитель матрицы, имеющий два одинаковых ряда, равен нулю.

Свойство № 4:

Общий множитель элементов какого-либо ряда определителя матрицы можно вынести за знак определителя.

Следствия из свойств № 3 и № 4:

Если все элементы некоторого ряда (строки или столбца) пропорциональны соответствующим элементам параллельного ряда, то такой определитель матрицы равен нулю.

Свойство № 5:

Если все элементы какой–либо строки или столбца определителя матрицы равны нулю, то сам определитель матрицы равен нулю.

Свойство № 6:

Если все элементы какой–либо строки или столбца определителя представлены в виде суммы 2-х слагаемых, то определитель матрицы можно представить в виде суммы 2-хопределителей по формуле:

Свойство № 7:

Если к какой–либо строке (или столбцу) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и тоже число, то определитель матрицы не изменит своей величины.

Миноры и алгебраические дополнения. Теорема Лапласа.

Миноры матрицы

Пусть дана квадратная матрица А, n - ого порядка. Минором некоторого элемента аij ,определителя матрицы n - ого порядка называется определитель (n - 1) - ого порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент аij. Обозначается Мij.

Рассмотрим на примере определителя матрицы 3 - его порядка:

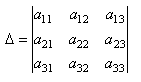
, тогда согласно определению минора, минором М12, соответствующим элементу а12, будетопределитель:

При этом, с помощью миноров можно облегчать задачу вычисления определителя матрицы. Надо разложить определитель матрицы по некоторой строке и тогда определитель будет равен сумме всех элементов этой строки на их миноры. Разложение определителя матрицы 3 - его порядка будет выглядеть так:

, знак перед произведением равен (-1)n, где n = i + j.

Алгебраические дополнения:

Алгебраическим дополнением элемента аij называется его минор, взятый со знаком "+", если сумма (i + j) четное число, и со знаком "-", если эта сумма нечетное число. Обозначается Аij. Аij = (-1)i+j × Мij.

Тогда можно переформулировать изложенное выше свойство. Определитель матрицы равен сумме произведение элементов некторого ряда (строки или столбца) матрицы на соответствующие им алгебраические дополнения. Пример:

Теорема ЛАПЛАСА

Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:

 (*)

(разложение по элементам i-й строки);

 (**)

(разложение по элементам j-го столбца).

Убедимся в справедливости теоремы Лапласа на примере определителя матрицы третьего порядка. Разложим его вначале по элементам первой строки

Что совпадает с определением определителя матрицы третьего порядка.

Разложение определителя по строке или столбцу. Определитель квазитреугольной матрицы.

 Разложение определителя 

     По элементам i-й строки:

     По элементам j-го столбца:

     Например, при n = 4 разложение по первой строке

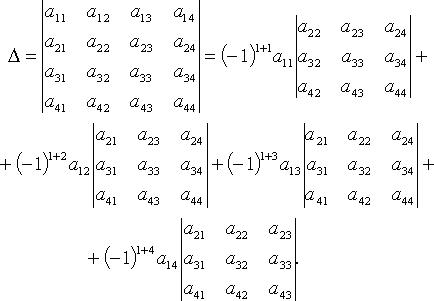
Квазитреугольная матрица

Квазитреугольной называется клеточная матрица A у которой клетки Aij = 0 при i > j (или i < j):

.

Определитель квазитреугольной матрицы равен произведению определителей диагональных клеток.

Обратная матрица

Если существуют квадратные матрицы Х и А, удовлетворяющие условию: X × A = A × X = E , где Е - единичная матрица того же самого порядка, то матрица Х называется обратной матрицей к матрице А и обозначается А-1. Всякая невырожденная матрица имеет обратную матрицу и притом только одну, т. е. для того чтобы квадратная матрица A имела обратную матрицу, необходимо и достаточно, чтобы её определитель был отличен от нуля.

Для получения обратной матрицы используют формулу:

, где Мji дополнительный минор элемента аji матрицы А.

Cвойства обратных матриц:

1) (А-1)-1 = А; 2) (АВ)-1 = В-1А-1; 3) (АТ)-1 = (А-1)Т;

Множество

  Множество - это совокупность объектов, рассматриваемая как одно целое. Основное отношение между элементом a и содержащим его множеством A обозначается так  (a есть элемент множестваA; или a принадлежит A, или A содержит a). Если a не является элементом множества A, то пишут  (a не входит в A, A не содержит a). Множество можно задать указанием всех его элементов, причем в этом случае употребляются фигурные скобки. Так {a, b, c} обозначает множество трех элементов. Аналогичная запись употребляется и в случае бесконечных множеств, причем невыписанные элементы заменяются многоточием. Так, множество натуральных чисел обозначается {1, 2, 3, ...}, а множество четных чисел {2, 4, 6, ...}, причем под многоточием в первом случае подразумеваются все натуральные числа, а во втором - только четные.

Эквивалентность.

Отношение эквивалентности (∼) на множестве X — это бинарное отношение, для которого выполнены следующие условия:

1. Рефлексивность:   для любого a в X,

2. Симметричность: если  , то  ,

3. Транзитивность: если   и  , то  .

Запись вида « » читается как «a эквивалентно b».

Геометрические векторы

Вектором в пространстве называется направленный отрезок, то есть такой отрезок, один из концов которого выделен и называется началом, а другой — концом. При этом сонаправленные и равные по длине отрезки считаются одним и тем же вектором

Направленным отрезком называется упорядоченная пара (A,B) точек пространства, у которой A называется началом, B — концом. Направленные отрезки (A,B) и (C,D) назовём эквивалентными, если   или если   и . Знак   обозначает сонаправленность:   если лучи   и   либо лежат на одной прямой и дают в пересечении луч, либо лежат на параллельных прямых в одной полуплоскости относительно прямой  . Классы эквивалентности по указанному отношению называются векторами.

Свободный вектор.

Два вектора называются равными, если они:

а) коллинеарны, одинаково направлены;

б) имеют равные длины.

Все нулевые векторы считаются равными друг другу.

Это определение равенства векторов характеризует так называемые свободные векторы. Данный свободный вектор можно переносить, не меняя его направления и длины, в любую точку пространства (откладывать от любой точки), при этом будем получать векторы, равные данному. Таким образом, свободный вектор определяет целый класс равных ему векторов, отличающихся только точкой приложения. 

Вектор на прямой, на плоскости, в пространстве

Пусть в пространстве дана прямая   и пересекающая ее плоскость  . Проекцией вектора  на прямую   параллельно плоскости   (вдоль плоскости  ) называется вектор  , началом которого служит проекция  , начала  , а концом — проекция   конца   вектора   (рис. 1.13,6). Если плоскость   перпендикулярна прямой  , то проекция называется ортогональной.

Проекция вектора на плоскость

Пусть в пространстве задана плоскость я и пересекающая ее прямая  .Проекцией вектора   на плоскость   параллельно прямой  (вдоль прямой  ) называется вектор  , началом которого служит проекция   начала  , а концом — проекция   конца   вектора  (рис. 1.14). Если прямая  перпендикулярна плоскости  , то проекция называется ортогональной.

Свойства проекций векторов

1. Проекции вектора на параллельные прямые (или на параллельные плоскости) равны.

2. Проекции равных векторов равны.

3. Проекция суммы векторов равна сумме их проекций.

4. Проекция произведения вектора на число равна произведению этого числа на проекцию вектора, другими словами, отношение коллинеарных векторов равно отношению их проекций (если оно определено).

5. Проекция линейной комбинации векторов равна линейной комбинации проекций

Введению в теорию линейных пространств

В дальнейшем через R обозначается поле вещественных чисел, через N — множество целых, а через N₊ — множество натуральных чисел. Вещественное векторное пространство (или, вещественное линейное пространство) представляет собой множество E элементов произвольной природы (его точки называются векторами ), в котором определены операции сложения векторов +: E × E → E и умножения на число · : R × E → E, удовлетворяющие следующим аксиомам: при всехx, y, z ∈ E и α, β ∈ R