17. Флуктуации термодинамических величин.

Флуктуация определяется дисперсией случайной величины

. (152) Здесь  - среднее значение случайной величины x,  - среднее значение ее квадрата. Флуктуацию удобнее определять среднеквадратичным значением

.

Пусть Q – обобщенная координата (параметр) классической системы погруженной в термостат при температуре T и F – обобщенная сила соответствующая обобщенной координате. Покажем, что дисперсия (или флуктуация) величины Q определяется формулой

. (153) Можно показать, что вероятность термодинамической системы погруженной в термостат и «открытой» по параметру Q определяется формулой

.

Здесь мы выразили величину Q через обычные координаты и импульсы. Статистический интеграл системы

.

Среднее значение Q

.

Дифференцируем среднее значение

После преобразования

. Что и требовалось доказать.

Применим формулу (153) для конкретных случаев.

 Задача. Определить флуктуации энергии системы в термостате при «замкнутых» остальных параметрах (объеме, числе частиц).

Формулу (153) можно представить в виде

. (153) Тогда для энергии «обобщенной силой» формально является величина . Используя (153), получаем

.

Для идеального одноатомного газа , поэтому

.

Среднеквадратичное отклонение

.

Относительная величина флуктуации энергии

.

 Задача. Определите флуктуацию объема системы погруженной в термостат и открытой по объему (фиксировано давление в системе, подвижный поршень).

В этом случае для объема сопряженной величиной (обобщенной силой) является (- p) «отрицательное» давление. В соответствии с общей формулой

.

Для идеального газа

.

Относительная среднеквадратичная флуктуация

 Задача. Определите флуктуацию числа частиц в системе погруженной в термостат и открытой по числу частиц. Объем в системе фиксирован.

Для числа частиц обобщенной силой является химический потенциал, поэтому

. (154) Для идеального газа

.

Отсюда . Значение производной подставляем в (154).

.

Относительная среднеквадратичная флуктуация

. (155)

 Задача. Определите флуктуацию угла поворота зеркала гальванометра. Считайте исполнительный механизм гальванометра термодинамической системой погруженной в термостат открытой по углу поворота.

Для угла поворота зеркала обобщенной силой является момент упругих сил . c – коэффициент упругости нити подвески зеркала. В соответствии с формулой (153)

Так как , то

.

Если гальванометр «не нагружен» током, то и

; .

Этот результат можно получить, используя теорему о равномерном распределении энергии по степеням свободы. Измерительная часть гальванометра является крутильным маятником, который имеет две термодинамические степени свободы (потенциальную и кинетическую).⁴⁰ Приравниваем среднюю потенциальную энергию маятника величине и получаем тот же результат.

. (156)

 Задача. Определите флуктуацию электрического заряда на обкладках конденсатора, которые замкнуты через сопротивление величиной R.

Обобщенной силой к величине заряда является напряжение, поэтому в соответствии с общей формулой (учитываем, что )

.

Учитывая, что , получаем

. (157)

 Задача. Используя результат предыдущей задачи, определите время разрядки конденсатора заряженного до напряжения U. Схема конденсатора погружена в термостат с температурой T.

Разряд конденсатора определяется формулой

.

Без учета дискретности заряда и термодинамики время разрядки конденсатора равно бесконечности. Учитывая термодинамику системы можно определить время разряда конденсатора по времени, при котором заряд конденсатора становится равным флуктуационному заряду, который определяется формулой (157). В соответствии с этим записываем

.

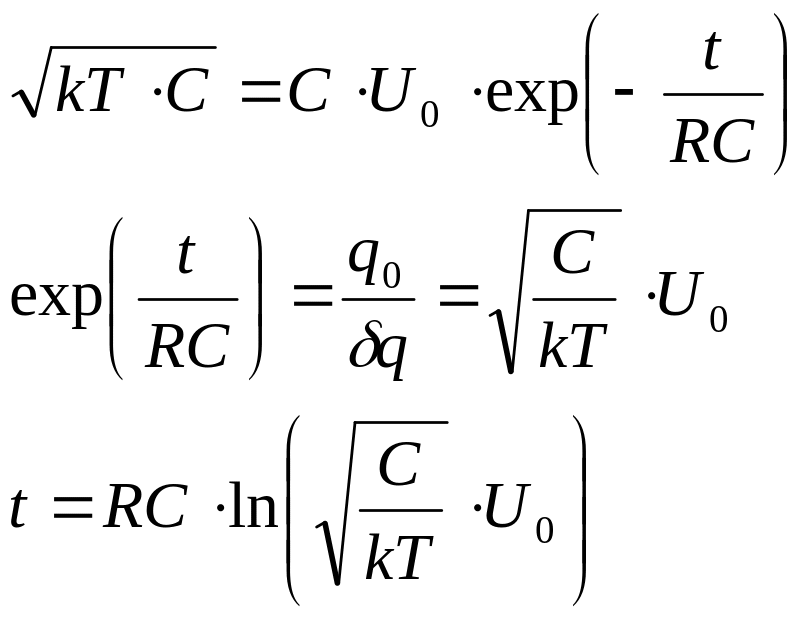Сделаем расчет для C = 1 мкФ, U₀ = 10 В, R = 100 кОм. В этом случае RC = 0,1 сек. q₀ = 10^-5 Кл.

.

2. Компьютерные задачи по статистической термодинамике.

Задача 1. Преобразовать равномерное распределение псевдослучайных чисел генерируемых программой RND к распределению . Эта функция плотности вероятности была получена в задаче «гравитационный кузнечик» (тело свободно падает в поле тяготения).

Задача 2. Преобразовать равномерное распределение псевдослучайных чисел генерируемых программой RND к линейной функции плотности вероятности (на интервале 0 – 1).

Задача 3. Провести компьютерное моделирование релаксации к равновесному распределению в неравновесном микроканоническом ансамбле (замкнутой системе). Неравновесное состояние представить линейным распределением вероятности состояний. Релаксацию проводить по максимуму энтропии.

Задача 4. Провести компьютерное моделирование методом Монте-Карло системы независимых спинов во внешнем поле (канонический ансамбль). Сравнить «экспериментальные» средние характеристики (энергия, флуктуация энергии) с теоретическими величинами.

Задача 5. Провести динамическое компьютерное моделирование системы «пружинный маятник + частица». Одномерная система. Маятник прикреплен к левой границе отрезка. Свободная частица «блуждает» в правой свободной области отрезка, упруго взаимодействуя с шариком маятника. Для введения «хаоса» в систему правая граница «флуктуирует» (ее положение случайным образом изменяется в небольшом интервале). Получить экспериментальные средние характеристики системы (энергии, координаты). Проверить теорему о равномерном распределении энергии по степеням свободы. Средняя энергия маятника имеющего две термодинамические степени свободы должна быть в два раза больше энергии свободной частицы.

Задача 6. Провести компьютерное моделирование методом Монте-Карло частицы на отрезке, который содержит потенциальную яму (канонический ансамбль). Сравнить экспериментальные средние величины (энергия, координата) с теоретическими величинами.

Задача 7. В среде MathCAD выполнить построение графиков (для различных температур) распределения Максвелла (функции плотности вероятности модуля скорости). Методом интегрирования проверить нормировку функции. Рассчитать характерные скорости молекул. Задание выполнить для воздуха ( ).

Задача 8. В среде MathCAD выполнить построение трехмерного графика приведенного уравнения Ван-дер-Ваальса. Получить двумерную матрицу значений давления. Провести его обработку при помощи программного модуля (обрезать по минимуму и максимуму).

Задача 9. В среде MathCAD выполнить построение графиков (для различных температур) функций Планка для теплового излучения. Проверить закон смещения Вина.

Задача 10. В среде MathCAD выполнить построение графиков функций теплоемкости кристаллов Эйнштейна и Дебая, низкотемпературной аппроксимации Дебая (кубический закон Дебая).

2. Приложение. Программы компьютерных заданий.

Задача 1.

Преобразование функции распределения проводим стандартным методом. Записываем дифференциальную вероятность

.

Для функции RND , поэтому

.

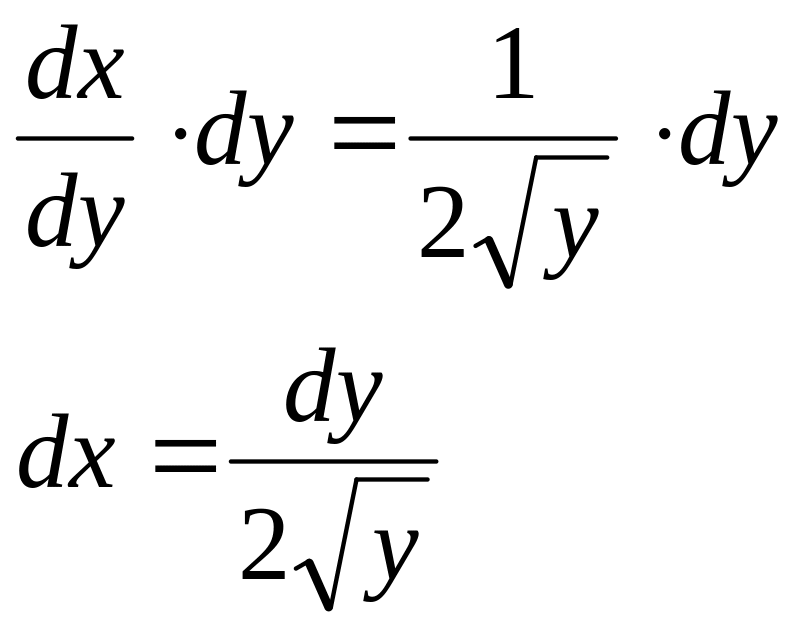Интегрируем.

.

При учете граничных условий находим, что Const = 0. Таким образом, функция преобразования имеет вид

и определена (нормирована) на отрезке 0 – 1. чтобы получить случайное число y нужно случайное число x выданное функцией RND возвести в квадрат.

.

Для проверки компьютерного моделирования вычислим средние характеристики.

.

Компьютерная программа и пример экспериментальных данных при моделировании.

'программа моделирования преобразования функции распределения вероятности

'преобразование равномерного распределния RND к 1/2/sqr(y)

n = 1000000'число шагов стат. эксперимента

FOR i = 1 TO n

x = RND

y = x ^ 2

ycp = ycp + y / n

y2cp = y2cp + y ^ 2 / n

NEXT

CLS

PRINT " ycp = ", ycp

PRINT " ycp0 = ", 1 / 3

PRINT " y2cp = ", y2cp

PRINT "y2cp0 = ", 1 / 5

Пример экспериментальных данных.

ycp = .3331939

ycp0= .3333333

y2cp = .1999727

y2cp0= .2

Средние значения теоретические и экспериментальные практически совпадают.

Задача 2.

Первоначально определяем константу в линейном распределении используя нормировку.

.

Далее решение задачи повторяет решение задачи 1. Записываем дифференциальную вероятность

.

Для функции RND , поэтому

.

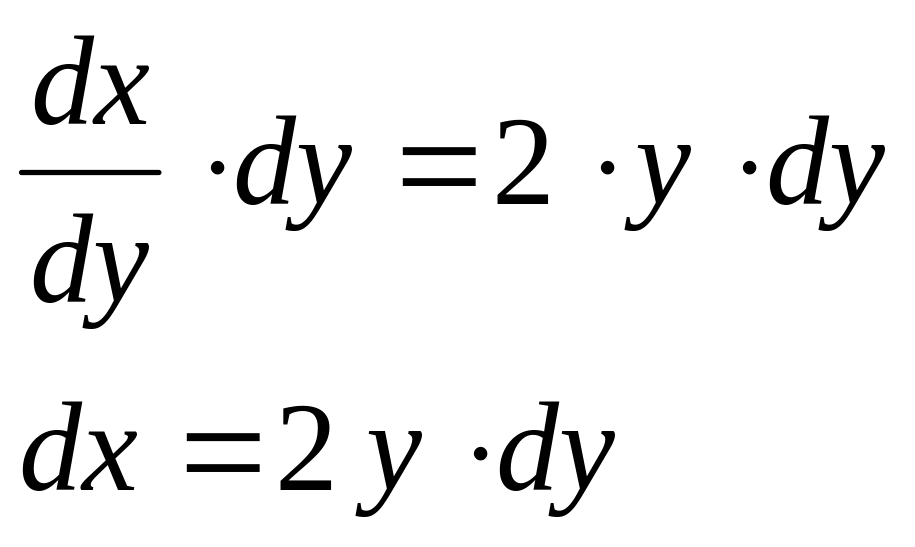Интегрируем

.

При учете граничных условий находим, что Const = 0. Таким образом, функция преобразования имеет вид

и определена (нормирована) на отрезке 0 – 1. чтобы получить случайное число y нужно из случайного числа x выданного функцией RND извлечь корень

.

Для проверки компьютерного моделирования вычислим средние характеристики.

.

Компьютерная программа аналогична предыдущей программе, поэтому приводим только пример экспериментальных данных.

ycp = .6665053

ycp0= .6666667

y2cp = .4998182

y2cp0= .5

Совпадение экспериментальных и теоретических средних характеристик говорит о правильном моделировании функции распределения.

Задача 3. Моделирование релаксации в микроканоническом ансамбле.

Релаксация проводится методом Монте-Карло по максимуму энтропии. Микроканонический ансамбль приводится к неравновесному состоянию. Вероятность первого состояния делается максимально возможной (например, 0,9), а остальные вероятности делаются одинаковыми и равными «по остатку» . Далее случайным образом выбирают одно из состояний и случайным же образом изменяют ее в небольшом интервале. Проверку изменения энтропии можно осуществить «по простому». Осуществить нормировку вероятностей и вычислить энтропию после «сдвига». Но удобнее воспользоваться дифференциальным методом определения вариации энтропии. Определим вариацию энтропии при вариации вероятностей.

.

.

Определим вариации вероятностей при изменении первой вероятности.

.

.

Подставляем эти формулы в общую формулу вариации энтропии.

.

Полученная формула позволяет без нормировки вероятностей определить вариацию энтропии при изменении на величину dP одной из вероятностей.

Программа и пример экспериментального моделирования.

'програма релаксации в микроканоническом ансамбле ↑

INPUT "число состояний n = ", n

DIM p(n)

p(1) = .9 'вероятность первого состояния

FOR i = 2 TO n 'цикл заполнения остальных вероятностей

p(i) = 1 / 10 / n

s = s - p(i) * LOG(p(i)) 'подсчет энтропии

NEXT

delt = .1 / n 'шаг изменения вероятностей

nstep = 1000000 'число шагов цепи Маркова

FOR j = 1 TO nstep 'цикл блуждания

i = INT(RND * n) + 1 'случайный выбор номера вероятности

dp = delt * (2 * RND - 1) 'изменение вероятности

p(i) = p(i) + dp

'страховка на отрицательность

IF p(i) <= 0 THEN p(i) = p(i) - dp: GOTO 1

ds = -dp * (s + LOG(p(i))) 'вариация энтропии

IF ds < 0 THEN p(i) = p(i) - dp: GOTO 1 'неудачный шаг

s = 0 'действия в случае удачного шага

summa = 0

FOR k = 1 TO n

p(k) = p(k) / (1 + dp)

s = s - p(k) * LOG(p(k))

summa = summa + p(k) 'сумма вероятностей для контроля

NEXT

1 NEXT

PRINT "энтропия s = ", s 'печать результатов

PRINT "энтропия равновесия s0 = ", LOG(n)

FOR i = 1 TO n

PRINT USING "#.####"; p(i)

NEXT

PRINT "сумма вероятностей summa = ", summa

Пример экспериментальных данных.

число состояний n = 10

энтропия s = 2.301872

энтропия равновесия s0 = 2.302585

0.0999

0.1000

0.1001

0.0999

0.0999

0.1000

0.0999

0.0999

0.0999

0.1000

сумма вероятностей summa = .9994525

После релаксации система пришла в состояние с равными вероятностями.

                                                                                

З адача 4. Моделирование канонического ансамбля системы независимых спинов.

'Программа: спины в термостате

INPUT "число спинов n=", n: DIM s(n)'ввод числа спинов и создание массива

e = 1 'энергия спина

INPUT "e/kT=", ekT 'ввод относительной температуры

FOR i = 1 TO n 'заполнение массива состояний (все вверх)

s(i) = 1

NEXT

nstep = 100000 'число МК шагов

n1 = n 'сколько спинов вверх

FOR j = 1 TO nstep 'цикл блуждания

i = INT(n * RND) + 1 'случайный выбор номера спина

dE = -2 * s(i) 'изменение энергии системы при повороте спина

'если энергия уменьшилась, то переворот остается и

'уменьшаем число спинов вверху, заканчиваем шаг

IF dE < 0 THEN s(i) = -s(i): n1 = n1 + dE / 2: GOTO 1

P12 = EXP(-dE * ekT) 'вероятность перехода при увеличении E

'разыгрывание вероятности перехода

IF RND <= P12 THEN s(i) = -s(i): n1 = n1 + dE / 2: GOTO 1

'подсчет среднего числа спинов вверху

1 n1cp = n1cp + n1 / nstep

NEXT

'печать результатов

PRINT "число спинов в верхнем состоянии n1cp=", n1cp

PRINT "в последний момент n=", n1

PRINT "среднее значение энергии системы Ecp=", 2 * n1cp - n

'теорет. значение энергии

E0 = -n * e * (EXP(ekT) - EXP(-ekT)) / (EXP(ekT) + EXP(-ekT))

PRINT "теоретическое значение энергии Ecp0=", E0

Пример экспериментальных результатов работы программы.

число спинов n = 10

e/kT=.01 высокая температура

число спинов в верхнем состоянии n1cp = 4.95226

в последний момент n1 = 6

среднее значение энергии системы Ecp = - 9,547901E-02

теоретическое значение энергии Ecp0 = - 9,999669E-02

спины разделились примерно поровну, энергия примерно равна нулю

число спинов n = 10

e/kT = 1 средняя температура

число спинов в верхнем состоянии n1cp = 1.197173

в последний момент n1 = 2

среднее значение энергии системы Ecp = -7.605654

теоретическое значение энергии Ecp0 = -7.615942

теоретические и экспериментальные значения практически совпадают

число спинов n=10

e/kT=10 низкая температура

число спинов в верхнем состоянии n1cp = .00103

в последний момент n1 = 0

среднее значение энергии системы Ecp = -9.99794

теоретическое значение энергии Ecp0 = -10

вверху нет спинов, они «сконденсировались» вниз, энергия минимальна

Задача 5. Проверка равномерного распределения энергии по термодинамическим степеням свободы.

'программа моделирования равномерного распределения по степеням свободы

'одномерная модель: на прямой маятник и частица

'левая граница случайно перемещается

pi = ATN(1) * 4

RANDOMIZE TIMER

m1 = 1: k = 8'масса частицы и коэффициент жесткости пружины маятника

INPUT "m2/m1= ", m2 'отношение масс

L = 1 'длина всего отрезка

x1 = 0: x2 = .8 'начальные координаты

v1 = SQR((2 - k * (L - x2) ^ 2) / m1) 'начальная скорость при E=1

v2 = 0: a2 = k * (L - x2) / m2 'ускорение частицы маятника

v0 = m1 * v1 / (m1 + m2) 'скорость центра масс

t = 2 * pi * SQR(m2 / k) 'период колебаний маятника, опорное время

nstep = 1000: dt = t / nstep 'число шагов и время шага

ni = nstep * 2000 'полное число шагов

E0 = 1 'начальная энергия

gr = 0 'левая граница

FOR i = 1 TO ni 'основной цикл движения

'сдвиг свободной частицы

x1 = x1 + v1 * dt

'флуктуация левой стенки и вкл. ключа после ее сдвига

IF x1 > .1 * L AND kl = 0 THEN gr = .05 * L * (2 * RND - 1): kl = 1

'отражение от левой границы

IF x1 < gr THEN x1 = 2 * gr - x1: v1 = ABS(v1): kl = 0

' предварительный сдвиг частицы маятника

dx2 = v2 * dt + a2 * dt ^ 2 / 2

'предсказание ускорения после сдвига

a22 = k * (L - x2 - dx2) / m2

'основной сдвиг частицы маятника

'во втором приближении с поправкой ускорения

x2 = x2 + v2 * dt + (a2 + a22) / 2 * dt ^ 2 / 2

'проверка удара, изменение скоростей и счетчик ударов

IF x1 > x2 THEN x1 = x2: v1 = 2 * v0 - v1: v2 = 2 * v0 - v2: n = n + 1

'половинка изменение скорости, определение ускорения, еще половинка

v2 = v2 + a2 * dt / 2: a2 = k * (L - x2) / m2: v2 = v2 + a2 * dt / 2

'вычисление энергии

E = m1 * v1 ^ 2 / 2 + m2 * v2 ^ 2 / 2 + k * (L - x2) ^ 2 / 2

'коэффициент изменения энергии из-за неточности алгоритма

kE = SQR(E0 / E)

'правка скоростей

v1 = v1 * kE: v2 = v2 * kE

'скорость центра масс

1 v0 = (m1 * v1 + m2 * v2) / (m1 + m2)

вычисление средних величин

x1cp = x1cp + x1 / ni: x2cp = x2cp + x2 / ni

x12cp = x12cp + x1 ^ 2 / ni: x22cp = x22cp + x2 ^ 2 / ni

E1cp = E1cp + m1 * v1 ^ 2 / 2 / ni

E2cp = E2cp + (m2 * v2 ^ 2 / 2 + k * (L - x2) ^ 2 / 2) / ni

NEXT

'печать средних величин

PRINT "E1cp=", E1cp, "E2cp=", E2cp, "E1cp+E2cp=", E1cp + E2cp, "E0=", E0

PRINT "E2cp/E1cp=", E2cp / E1cp

PRINT "x1cp=", x1cp, "x2cp=", x2cp

PRINT "dx1=", SQR(x12cp - x1cp ^ 2), "dx2=", SQR(x22cp - x2cp ^ 2)

PRINT "число ударов n=", n

Пример экспериментальных данных при равных массах. 6 измерений.

m2/m1= 1

E1cp= .3159674 E2cp= .6823276 E1cp+E2cp=

.9982951 E0= 1

E2cp/E1cp= 2.159487

x1cp= .5253313 x2cp= 1.079103

dx1= .3461974 dx2= .2806781

число ударов n= 2724

m2/m1= 1

E1cp= .3455153 E2cp= .6537001 E1cp+E2cp=

.9992154 E0= 1

E2cp/E1cp= 1.891957

x1cp= .5507061 x2cp= 1.085436

dx1= .3515712 dx2= .2743936

число ударов n= 2265

m2/m1= 1

E1cp= .3205802 E2cp= .6790064 E1cp+E2cp=

.9995866 E0= 1

E2cp/E1cp= 2.118055

x1cp= .530637 x2cp= 1.080149

dx1= .3483114 dx2= .2804278

число ударов n= 2415

m2/m1= 1

E1cp= .3297172 E2cp= .6685681 E1cp+E2cp=

.9982853 E0= 1

E2cp/E1cp= 2.027701

x1cp= .5392638 x2cp= 1.081812

dx1= .3520854 dx2= .2787308

число ударов n= 2898

m2/m1= 1

E1cp= .3296842 E2cp= .6694469 E1cp+E2cp=

.9991311 E0= 1

E2cp/E1cp= 2.03057

x1cp= .5377797 x2cp= 1.082206

dx1= .3501166 dx2= .2787733

число ударов n= 2197

m2/m1= 1

E1cp= .3405819 E2cp= .6587474 E1cp+E2cp=

.9993293 E0= 1

E2cp/E1cp= 1.934182

x1cp= .5453964 x2cp= 1.084372

dx1= .3496881 dx2= .2758292

число ударов n= 2245

Среднее значение отношения энергий⁴¹

Задача 6. Частица на отрезке с потенциальной ямой. Система погружена в термостат.

Статистическая сумма системы.

.

Средняя энергия

.

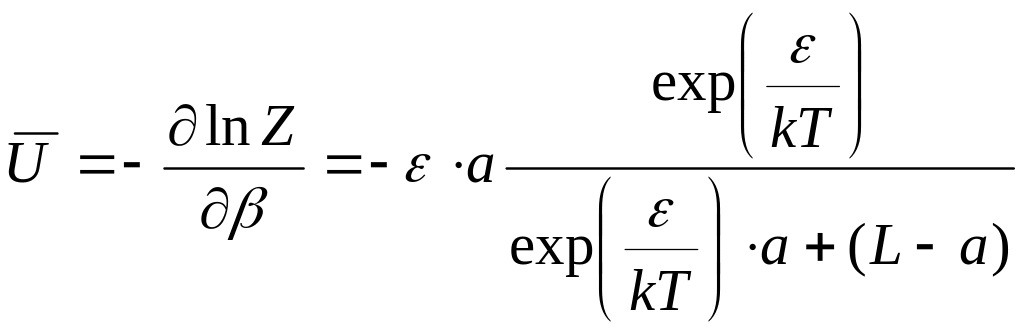Среднее значение координаты.

.

'программа: частица на отрезке с потенциальной ямой

'канонический ансамбль

L = 1 'размер отрезка

INPUT "относительный размер ямы a/L = ", aL

a = L * aL

e = 1 'глубина ямы

INPUT "относительная температура e/kT = ", ekT

nstep = 1000000 'число шагов цепи Маркова

delt = L / 10 'размер области разыгрывания сдвига

x = a / 2 'начальная координата частицы

U = -e 'потенциальная энергия

FOR i = 1 TO nstep 'цикл блуждания

dx = delt * (2 * RND - 1) 'сдвиг частицы

x = x + dx

IF x < 0 THEN x = -x 'отражение от левой стенки

IF x > L THEN x = 2 * L - x 'отражение от правой стенки

IF x <= a THEN U1 = -e ELSE U1 = 0 'определение энергии

p12 = EXP(-(U1 - U) * ekT) 'переходная вероятность

IF RND >= p12 THEN x = x - dx: GOTO 1 'разыгрывание перехода

k = k + 1: U = U1 'счетчик удачи, энергия

1 xcp = xcp + x / nstep 'подсчет средних величин

Ucp = Ucp + U / nstep

NEXT

'печать результатов

PRINT "средняя потенциальная энергия Ucp = ", Ucp

U0 = -e * a * EXP(ekT) / (a * EXP(ekT) + (L - a))

PRINT "теорет. значение энергии Ucp0= ", U0

PRINT "среднее значение координаты xcp = ", xcp

x0 = (a ^ 2 / 2 * (EXP(ekT) - 1) + L ^ 2 / 2) / (a * EXP(ekT) + (L - a))

PRINT "теорет. значение ср. координаты xcp0 = ", x0

PRINT "коэффициент сдвига k=nуд/nstep=", k / nstep

Пример экспериментальных данных.

относительный размер ямы a/L = .5

относительная температура e/kT = .01

средняя потенциальная энергия Ucp = -.5146065

теорет. значение энергии Ucp0= -.5024999

среднее значение координаты xcp = .4932805

теорет. значение ср. координаты xcp0 = .49875

коэффициент сдвига k = nуд/nstep= .999753

Высокая температура. Частица с вероятностью 1/2 локализована в яме.

относительный размер ямы a/L = .5

относительная температура e/kT = 1

средняя потенциальная энергия Ucp = -.7415845

теорет. значение энергии Ucp0= -.7310586

среднее значение координаты xcp = .3806343

теорет. значение ср. координаты xcp0 = .3844707

коэффициент сдвига k = nуд/nstep= .977007

Средняя температура. Теоретические и экспериментальные значения практически совпадают.

относительный размер ямы a/L = .5

относительная температура e/kT = 10

средняя потенциальная энергия Ucp = -1.009037

теорет. значение энергии Ucp0= -.9999546

среднее значение координаты xcp = .2486781

теорет. значение ср. координаты xcp0 = .2500227

коэффициент сдвига k = nуд/nstep= .950508

Низкая температура. Частица «сидит» в яме.

1 Нужное соотношение получается с использованием закона сохранения энергии.

2 Пример. Вероятность того, что при N бросках монеты «орел» выпадет n раз. Очевидно, что при большом N эта вероятность будет максимальна при n = Np = N0,5 = N/2.

3 Пример. Вероятность того, что за время t произойдет n радиоактивных распадов. Это распределение можно назвать «полудискретным» или смешанным. Процесс определен дискретной (n – число распадов) и непрерывной (t – временной интервал) величинами.

4 И.П. Базаров вводит постулаты термодинамики: 1 – постулат о термодинамическом равновесии (общее начало термодинамики); 2 – постулат - о существовании температуры («его иногда называют нулевым началом…»). В некоторых учебниках (см. Р. Кубо) «нулевое начало» - это закон транзитивности теплового равновесия. В учебнике И.А. Квасникова. «Для каждой термодинамической системы существует состояние термодинамического равновесия, которого она при фиксированных внешних условиях с течением времени самопроизвольно достигает. Сформулированный тезис составляет так называемое нулевое начало термодинамики.»

5 Частицей может быть и фотон.

6 В равновесной системе отсутствуют потоки. Система может состоять и из одной частицы, которая «погружена» в термостат. В этом случае ее температура формально равна температуре термостата.

7 Параметр независящий от размеров системы является интенсивным. (К интенсивным параметрам относятся и удельные параметры: плотность, удельная энергия, удельная теплоемкость…).

8 штрих отмечает «недифференциальность» величин. Одно и тоже изменение энергии можно получить различным «весом» слагаемых теплоты и работы. Первый закон в дифференциалах для газа может выглядеть так .

9 Уточнение определения  будет дано после введения термодинамических потенциалов.

10 В этой форме все слагаемые записаны через дифференциалы.

11 Р. Кубо. Теорема Нернста-Планка. Следствия: недостижимость абсолютного нуля, теплоемкость, коэффициент теплового расширения и некоторые другие аналогичные величины стремятся к нулю.

12 В дальнейших формулах будем использовать мольную теплоемкость.

13 Математическая безразмерная энтропия определяется . Знак минус необходим для положительной определенности.

14 Ансамбль – совокупность большого количества систем.

15 Без множителя Лагранжа можно обойтись следующим образом. Выделим в сумме (14) первое слагаемое . Будем считать вариации вероятностей произвольными (независимыми) кроме первой, которую определим из условия нормировки . Подставим в предыдущее уравнение. . Объединяем суммы . В этом выражении все вариации независимы, и оно должно выполняться тождественно. Поэтому получаем .

16 Число квантовых состояний может зависеть от числа частиц в системе.

17 И квантовую формулу энергии можно записать по классической схеме

18 ; - сокращенные записи.

19 При записи результата интегрирования используем приближенную формулу Стирлинга .

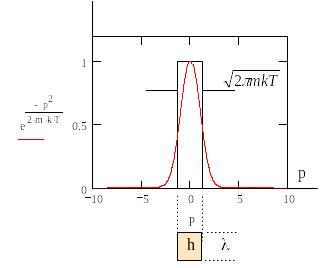
20 Смысл тепловой длины волны состоит в следующем. Интеграл импульсной гауссовой экспоненты определяет эффективную ширину импульсной области (так как максимум функции интегрирования равен 1). Ели теперь на основе этой импульсной эффективной ширины вычислить линейный размер квантовой фазовой ячейки, то и получим «тепловую длину» . ³ – определяет геометрическую часть трехмерной квантовой фазовой ячейки. .

21 Для системы в термостате.

22 В некоторых учебниках «Распределение Максвелла-Больцмана».

23 Можно записать через импульсы и координаты .

24 «Нормальным» называют вещество, которое при плавлении увеличивает свой объем.

25 Поверхность называют линейным гиперболоидом.

26 Газ при температуре ниже критической принято называть паром.

27 Критическая изотерма это след от сечения фазовой диаграммы плоскостью PV, которая касается двухфазной области жидкости и насыщенного пара. Точка касания называется критической точкой. На графике PV критическая точка является точкой перегиба.

28 Einstein A. – Ann. Physic, 22, 180, (1907).

29 Debye P. – Ann. Physic, 39, 789 (1912).

30 Для фермионов существует запрет Паули: в одном квантовом состоянии может находиться только одна частица. Для бозонов такого ограничения нет.

31 .

32 И убеждаемся, что  в первом приближении действительно малая величина при малой плотности газа и высокой температуре.

33 Закон степени 3/2 не согласуется с экспериментальными данными по жидкому гелию. Эксперимент дает зависимость примерно 11/2. (Исихара)

34 Бозоны при нулевой температуре все располагаются на первом энергетическом уровне.

35 В пространстве квантовых чисел фермионы находятся внутри 1/8 объема энергетического шара.

36 Ч. Киттель.

37 Sommerfeld A., Zs. Phys., 47, 1 (1928)

38 При низкой температуре нижний предел достаточно «большая» отрицательная величина.

39 Формулы (149) и (150) справедливы только при низких температурах.

40 Следует отметить различие между понятиями: степень свободы механическая и степень свободы термодинамическая. Число степеней свободы с точки зрения механики – это число обобщенных координат однозначно определяющих положение механической системы. Для колебательных систем это число определяет число собственных частот колебаний. Число термодинамических (энергетических) степеней свободы равно числу слагаемых в энергетической сумме. Крутильный маятник имеет одну механическую степень свободы и две термодинамические степени свободы. Результат (156) можно интерпретировать следующим образом. Полную энергию поворота приравниваем kT – тепловой энергии двух степеней свободы. . При гармоническом колебании среднее значение квадрата угла поворота связано с квадратом амплитуды известным соотношением . Делаем замену и получаем .

41 Без учета коэффициента Стьюдента.