Задачи математической статистики. Генеральная и выборочная совокупности. Виды статистического распределения: дискретный и интервальный статистические ряды. Гистограмма. Числовые характеристики статистических рядов.
Задачи математической статистики
1. Определение закона распределения случайной величины (путем построения гистограмм).
2. Нахождение числовых характеристик случайной величины (среднего арифметического, среднего квадратического отклонения, ошибки среднего).
3. Проверка научных гипотез (например, оценка достоверности различий средних значений в опытной и контрольной группах).
Основные понятия математической статистики
Генеральная совокупность – это совокупность всех значений данной случайной величины.
Примеры:
• Рост мужчин
• Рост женщин
• Значения систолического артериального давления
• Концентрация эритроцитов в крови обследуемых
Количество
элементов ГС
, т.е. стремится к бесконечности.
Поэтому, для изучения свойств ГС отбирают часть ее элементов – выборку.
Выборка (выборочная совокупность) - это часть ГС, выбираемая для статистической обработки.
ПРАВИЛА СОЗДАНИЯ ВЫБОРКИ:
1. Случайность отбора (например, при оценке роста женщин нельзя отдавать предпочтение блондинкам, или полным, и т.д.)
2. Репрезентативность (представительность). Например, при оценке доходов жителей Москвы нужно отбирать жителей из разных районов города.
3. Достаточный объем выборки.
Простой (дискретный) статистический ряд. Дискретность – прерывность, противопоставляется непрерывности. Например, дискретное изменение какой-либо величины во времени — это изменение, происходящее через определённые промежутки времени (скачками).
Пример:
160 175 168 175 180 196 178 174 198
n (количество элементов) = 9
160 |
168 |
174 |
175 |
178 |
180 |
196 |
198 |
1 |
1 |
1 |
2 |
1 |
1 |
1 |
1 |
Интервальный статистический ряд (удобен при построении гистограмм) - это совокупность интервалов вариант и относительных частот попадания их в эти интервалы, нормированных к ширине интервалов.
Отрезок
числовой оси, на котором содержатся
значения выборки, разбивают на N интервалов
шириной
каждый.
(формула
Старджеса)
Определяют
частоту встречаемости значений случайной
величины в
в каждом интервале
,
рассчитывают относительную частоту
встречаемости в каждом интервале
и делят на ширину интервала
,
величина
/
приближенно равна
.
Строят гистограмму, которая является
приближенным отображением функции
.
Для наглядности статистические распределения изображают графически в виде полигона или гистограммы.
Полигон
частот
– ломаная линия, отрезко которой
соединяют точки с координатами
или
для полигона относительных частот – с
координатами
Гистограмма
частот – совокупность смежных
прямоугольников, построенных на одной
прямой линии, основания прямоугольников
одинаковы и равны
,
а высоты равны отношению частоты (или
относительной частот) к
:
, где
– сумма частот вариант.
Наиболее распространенными числовыми характеристиками статистического распределения являются средние величины: мода, медиана и средняя арифметическая, или выборочная средняя.
Мода
(
)
равна варианте, которой соответствует
наибольшая частота. В случае приведенного
выше варианта дискретного статистического
ряда,
= 175.
Медиана
равна варианте, которая расположена в
середине статистического распределения.
Она делит статистический (вариационный)
ряд на две равные части. При четном числе
вариант за медиану принимают среднее
значение на двух центральных вариант.
В рассмотренном распределении
= 175.
Выборочная
средняя
.
Определяется
как среднее арифметическое значение
вариант статистического ряда:
Для
характеристики рассеяния вариант вокруг
своего среднего значение
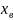вводят характеристику, называемую
выборочной
дисперсий
,
- среднее арифметическое квадратов
отклонения вариант от их среднего
значения:
На примере нашего ряда:
Квадратный корень из выборочной дисперсии называют выборочным средним квадратическим отклонением:
На нашем примере:
Интервальная оценка генеральной средней по выборке (большой и малой). Доверительный интервал. Доверительная вероятность.
При изучении генеральной совокупности исходят из того, что рассматриваемый признак имеет непрерывное распределение по нормальному закону с плотностью вероятности (распределения) .
Генеральное
среднее (
)
-
среднее арифметическое значение всех
величин, составляющих ГС:
Генеральная
дисперсия (
)
- рассеяние
значений изучаемого признака ГС от их
:
Генеральное
среднее квадратическое отклонение (
):
Как правило, и неизвестны. Поэтому используются две оценки: точечная и интервальная.
Точечная оценка:
- из генеральной совокупности делают разные выборки;
- для выборок
рассчитывают
и
;
- выборочные оценки и называют точечными;
- недостаток точечной оценки: при малой выборке может сильно отличаться от истинных параметров ГС.
Однако, при неограниченном увеличении объема выборки ( ):
Интервальная оценка:
- компенсирует недостатки точечной оценки;
- указывают
доверительный
интервал
(доверительные границы), в котором с
определенной (доверительной)
вероятностью
находится генеральная средняя
;
Доверительная вероятность определяет вероятность, с которой осуществляются следующие неравенства:
– положительное
число, полуширина интервала, характеризует
точность оценки.
Кроме
доверительной вероятности используется
противоположное понятие – уровень
значимости
– выражает вероятность непопадания
генеральной средней в доверительный
интервал.
Для большой выборки точность оценки определяется по формуле:
Где
– обозначение выражения
,
– генеральное среднее квадратичное
отклонение.
На
практике, при нахождении доверительного
интервала по этим формулам, берут
выборочную среднюю (
)
некоторой конкретной выборки (объем
),
а вместо генеральной средней квадратичной
(
)
используют выборочную среднюю квадратичную
этой же выборки (
).
τ находится через таблицу функции нормального распределения Ф и через формулу
Откуда
На данном изображении таблицы нормального распределения Z = τ.
Для
примера найдем значение неравенства
для нашей выборки, представленной выше.
Возьмем доверительную вероятность
.
Имеем:
;
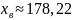Получаем:
Находим наиболее близкие или такие же значения по таблице функции, складываем значения столбцов:
Подставляем значения, получаем неравенство:
Формально, наша выборка была слишком мала для подобной интервальной оценки.
При
достаточно большой выборке можно сделать
надежные выводы о генеральной средней.
Но при малой
выборке (
)
в выражении доверительного интервала
(
)
точность оценки определяется по следующей
формуле:
Где
– параметр, называемый коэффициентом
Стьюдента (его находят по таблице для
указанной доверительной вероятности),
– выборочное
среднее квадратическое отклонение,
– объем выборки,
– полуширина интервала, характеризующая
точность оценки.
На
примере вышеуказанного статистического
ряда мы уже нашли
;
;
.
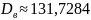Задав доверительную вероятность 0,98,
находим коэффициент
= 2,9 (объем выборки
).
Подставив эти данные в имеющееся
неравенство, получаем:
Можно сравнить большую и малую выборки.
Стандартная ошибка среднего (термин был впервые введен Юлом, 1897) это теоретическое стандартное отклонение всех средних выборки размера , извлекаемое из совокупности, и зависящая от совокупной дисперсии и размера выборки, выглядит следующим образом:
