Глава IV

Преобразование схем электрических цепей

4-1. ПОСЛЕДОВАТЕЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЯ

При расчете электрических цепей часто возникает целесообразность преобразования схем этих целей в более простые и удобные для расчета. Так, например, при одном или нескольких источниках электрической энергии в ряде случаев удается преобразовать электрическую схему в одноконтурную или в схему с двумя узлами, что весьма упрощает последующий расчет.

Описываемые ниже приемы преобразования схем электрических цепей применимы для цепей постоянного и переменного тока; ради общности изложения они приводятся в комплексной записи.

Одним из основных видов преобразования электрических схем, часто применяемых на практике, является преобразование схемы со смешанным соединением элементов. Смешанное соединение элементов представляет собой сочетание более простых соединений - последовательного и параллельного, рассмотрению которых и посвящен данный параграф. Смешанное соединение разбирается в § 4-2.

Последовательное соединение

На рисунке 4-1 изображена ветвь электрической цепи, в которой последовательно включены комплексные сопротивления Z₁, Z₂, ..., Z_n. Через все участки цепи, соединенные последовательно, проходит один и тот же ток .

Напряжения на отдельных участках цепи обозначены

через , ,… .

По второму закону Кирхгофа

или, что то же,

Сумма комплексных сопротивлений всех последовательно соединенных участков цепи

называется эквивалентным комплексным сопротивлением.

Рисунок 4-1. Последовательное соединение

Рисунок 4-2. Последовательное соединение однородных звеньев

Если мнимые части комплексного сопротивления

представляют собой сопротивления одинакового характера - индуктивного или емкостного (рисунок 4-2), то эквивалентное комплексное сопротивление Z находится в результате арифметического сложения в отдельности сопротивлений R_k, индуктивностей L_k или величин 1/C_k, обратных емкостям:

или

где

Ток в цепи равен:

Напряжения на участках цепи, соединенных последовательно, относятся как комплексные сопротивления этих участков: напряжение на k-м участке равно произведению суммарного напряжения на отношение комплексного сопротивления k-го участка к эквивалентному комплексному сопротивлению цепи:

.

Приведенные выше формулы справедливы при любых значениях Z_k.

Параллельное соединение

На рисунке 4-3 изображена схема электрической цепи с двумя узлами. Между этими узлами параллельно соединены ветви с комплексными проводимостями Y₁, Y₂,…, Y_n. Напряжение па всех ветвях одинаковое, равное .

Рисунок 4-3. Параллельное соединение

Токи в ветвях обозначены через , ,… . По первому закону Кирхгофа

или, что то же,

Сумма комплексных проводимостей всех ветвей, соединенных параллельно,

называется эквивалентной комплексной проводимостью.

Рисунок 4-4. Параллельное соединение однородных звеньев

Если мнимые части комплексов Y_k = g_k - jb_k представляют собой проводимости одинакового характера — емкостного или индуктивного (рисунок 4-4), то эквивалентная комплексная проводимость Y находится в результате арифметического сложения отдельных активных проводимостей g_k, емкостей C_k, или величии 1/L_k, обратных индуктивностям:

или

где

Суммарный ток в цепи равен:

.

Токи в ветвях относятся, как их комплексные проводимости: ток в k-й ветви равен произведению суммарного тока всех ветвей на отношение комплексной проводимости k-й ветви к эквивалентной комплексной проводимости:

Данным выражением особенно удобно пользоваться при n>2. При этом значения Y_k могут быть любыми.

В случае параллельного соединения двух ветвей (n = 2) обычно пользуются выражениями, в которые входят сопротивления Z₁ = 1/Y₁ и Z₂ = l/Y₂ ветвей; эквива­лентное комплексное сопротивление равно:

Токи в параллельных ветвях:

т.е. ток одной из двух параллельных ветвей равен суммарному току, умноженному на сопротивление другой ветви и деленному на сумму сопротивлений обеих ветвей.

4-2. СМЕШАННОЕ СОЕДИНЕНИЕ

Электрические схемы, имеющие смешанное соединение, могут быть преобразованы в более простую электрическую схему путем замены параллельных ветвей одной ветвью и соответственно последовательно соединенных участков цепи - одним участком.

На рисунке 4-5 показан пример электрической цепи со смешанным соединением. Эта схема легко приводится к одноконтурной. Первоначально вычисляется эквивалентная комплексная проводимость

Рисунок 4-5. Смешанное соединение

параллельных ветвей; затем находится величина, обратная проводимости, т.е. общее комплексное сопротивление параллельных ветвей; найденное комплексное сопротивление суммируется с комплексным сопротивлением последовательно включенного участка. Полученное суммарное комплексное сопротивление эквивалентно со­противлению исходной цепи со смешанным соединением.

Рисунок 4-6 Цепная схема

Расчетные выражения для рассматриваемого случая будут следующие:

Суммарное комплексное сопротивление всей цепи равно:

а суммарный ток

Токи в ветвях относятся, как комплексные проводимости ветвей:

Таким образом, многоконтурная электрическая схема со смешанным соединением приводится к одноконтурной, имеющей суммарное комплексное сопротивление Z или соответственно суммарную комплексную проводимость Y. Распределение токов и напряжений в смешанной цепи подчиняется правилам, указанным в предыдущем параграфе.

Описанный выше порядок преобразования схемы и нахождения распределения токов принципиально применим и для так называемой цепной схемы, показанной на рисунке 4-6. Просуммировав комплексные сопротив-(страница)

Если исходной является схема рисунока 4-7,б и заданными параметрами являются R₂, L₂ и ω, то параметры эквивалентной цепи (рисунок 4-7, а) определятся из выражении:

Из полученных выражений видно, что числовые значения R₁ и L₁ эквивалентной цепи зависят от частоты.

Условия эквивалентности для цепей с последовательным и параллельным соединением сопротивления и емкости имеют вид:

При достаточно высокой частоте (ωC₂R₂)²>>1, и тогда

4-4. ПРЕОБРАЗОВАНИЕ ТРЕУГОЛЬНИКА В ЭКВИВАЛЕНТНУЮ ЗВЕЗДУ

Преобразованием треугольника в эквивалентную звезду называется такая замена части цепи, соединенной по схеме треугольником, цепью, соединенной по схеме звезды, при которой токи и напряжения в остальной части цепи сохраняются неизменными. Иначе говоря, эквивалентность треугольника и звезды понимается в том смысле, что при одинаковых напряжениях между одноименными зажимами токи, входящие в одноименные зажимы, одинаковы. Это равносильно тому, что мощности в этих цепях одинаковы.

На рисунке 4-8 показан случай, когда преобразование треугольника в эквивалентную звезду дает возможность преобразовать многоконтурную схему в одноконтурную.

Для вывода расчетных выражений, служащих для преобразования треугольника в эквивалентную звезду, ниже приняты следующие обозначения (рисунок 4-9):

Z₁₂, Z₂₃, Z₃₁ — сопротивления сторон треугольника;

Z₁, Z₂, Z₃ — сопротивления лучей звезды;

, , — токи, подходящие к зажимам 1, 2, 3;

, , — токи в ветвях треугольника.

Рисунок 4-8. Упрощение схемы преобразованием треугольника в звезду.

Рисунок 4-9. Соединения треугольником (а) и звездой (б).

Выразим токи в ветвях треугольника через приходящие токи.

По второму закону Кирхгофа сумма напряжений в контуре треугольника равна нулю:

По первому закону Кирхгофа для узлов 2 и 1

Решение этих уравнений относительно дает:

Напряжение между зажимами 1 и 2 схемы рисунок 4-9, а будет:

а в схеме рисунок 4-9, б оно равно:

Для эквивалентности необходимо равенство напряжений при всяких токах и , т.е.

Это возможно при условии:

Третье выражение получается в результате круговой замены индексов.

Итак, комплексное сопротивление луча звезды равно произведению комплексных сопротивлений прилегающих сторон треугольника, деленному на сумму комплексных сопротивлений трех сторон треугольника.

Выше было получено выражение для тока в стороне 1-2 треугольника в зависимости от токов и . Круговой заменой индексов можно получить токи в двух других сторонах треугольника;

4-5. ПРЕОБРАЗОВАНИЕ ЗВЕЗДЫ В ЭКВИВАЛЕНТНЫЙ ТРЕУГОЛЬНИК

В расчетах также возникает необходимость замены звезды эквивалентным треугольником. На рисунок 4-10 показан, например, случай, когда такая замена позволяет преобразовать сложную электрическую схему в одноконтурную.

При переходе от звезды к треугольнику заданными являются сопротивления звезды Z₁,Z₂,Z3.

Рисунок 4-10. Упрощение схемы преобразованием звезды в треугольник.

Выражения для искомых сопротивлений треугольника находятся в результате совместного решения трех уравнений (4-1),

Деление третьего уравнения на первое, а затем на второе дает:

Выражая отсюда Z₂₃ и Z₃₁ через Z₁₂ и подставляя их в первое уравнение (4-1), получим:

откуда

Аналогично круговой заменой индексов получим:

Следовательно, комплексное сопротивление стороны треугольника равно сумме комплексных сопротивлений прилегающих лучей звезды и произведения их, деленного на сопротивление третьего луча.

Токи в лучах звезды легко выражаются через токи в сторонах треугольника. С учетом положительных направлений на рисунок 4-9 имеем

4-6. ЭКВИВАЛЕНТНЫЕ ИСТОЧНИКИ НАПРЯЖЕНИЯ И ТОКА

Два разнородных источника электрической энергии — источник напряжения и источник тока — считаются эквивалентными, если при замене одного источника другим токи и напряжения во внешней электрической цепи, с которой эти источники соединяются, остаются неизменными. На рисунке 4-11 изображены эквивалентные источники напряжения и тока, посылающие во внешнюю цепь ток и поддерживающие на своих зажинах одинаковое напряжение .

Условием эквивалентности источников, именуемым в дальнейшем правилом об эквивалентных источниках напряжения и тока, служит следующее соотношение между э. д. с. источника напряжения и током источника тока:

(4.3)

где Z — внутреннее комплексное сопротивление как источника напряжения, так и источника тока.

Действительно, напряжение на зажимах источника напряжения получается в результате вычитания из э. д. с. падения напряжения от тока в комплексном сопротивлении Z источника (рисунок 4-11,а).

Соответственно напряжение на зажимах источника тока при той же величине тока посылаемого во внешнюю цепь, равно падению напряжения от тока в комплексном сопротивлении Z источника (рисунок 4-11,б). В обоих случаях напряжения на зажимах источника одинаковы:

т. е. получается условие (4-3), не зависящее от тока нагрузки.

При отсоединении эквивалентных источников напряжения и тока от внешней цепи (I₁ = 0) напряжение на зажимах обоих источников равно . Именно это обстоятельство и равенство внутренних комплексных сопротивлений обоих источников и обеспечивают их эквивалентность при любом режиме работы (см. § 7-9).

Следует заметить, что мощности, расходуемые во внутренних сопротивлениях эквивалентных источников напряжения и тока, неодинаковы. В первом случае полная мощность, расходуемая в источнике, равна , во

втором случае

Рисунок 4-11. Эквивалентные источники напряжения (а) и тока (б).

Например, при отсоединении источников от внешней цепи в первом случае мощность в источнике не расходуется, а во втором случае она составляет .

Поэтому эквивалентность источников следует понимать только в смысле неизменности токов, напряжений и мощностей во внешней электрической цепи, присоединенной к источникам.

Если внутреннее сопротивление источника напряже­ния равно нулю, то непосредственное применение формулы (4-3) для нахождения эквивалентного источника тока по заданной величине э. д. с. источника не представляется возможным. В таких случаях сопротивление внешней цепи, включенной последовательно с э. д. с, можно рас­сматривать в качестве внутреннего сопротивления источ­ника, что позволит применить формулу (4-3).

В случае сложной электрической цепи замена источника напряжения эквивалентным источником тока или обратно может иногда упростить расчет.

Целесообразность такой замены проиллюстрирована, в частности, в следующем параграфе.

4-7. ПРЕОБРАЗОВАНИЕ СХЕМ С ДВУМЯ УЗЛАМИ

Применим правило об эквивалентных источниках напряжения и тока к преобразованию схемы с параллельным соединением n ветвей, содержащих источники напряжения (рисунок. 4-12,а).

Заменяя заданные источники напряжения источниками тока, получаем схему рисунок 4-12,б. Источники тока в совокупности образуют эквивалентный источник тока

Рисунок 4-12. Преобразование параллельного соединения ветвей с источниками напряжений.

(рисунок 4-12, в), причем

Пользуясь этим соотношением, можно в конечном итоге перейти от схемы в к схеме г, являющейся эквивалентом исходной схемы а. Здесь

Таким образом, n параллельных ветвей с источниками напряжения между двумя узлами могут быть заменены одним источником тока (рисунок 4-12, в) или источником напряжения (рис. 4-12, г).

Ток во внешней цепи (в ветви с сопротивлением Z_n+1) равен:

Напряжение между двумя узлами находится по формуле

Выведенные здесь выражения широко используются для расчета электрических цепей с двумя узлами, а также более сложных цепей, приводящихся к двум узлам.

4-8. ПЕРЕНОС ИСТОЧНИКОВ В СХЕМЕ

Расчет электрической цепи облегчается в ряде случаев в результате переноса в схеме источников э. д. с. или тока. Как это видно из уравнений Кирхгофа, токи в схеме определяются заданными величинами суммарных э. д. с. в контурах независимо от того, из каких отдельных сла­гающих они состоят. Поэтому изменение расположения в схеме источников э. д. с, при котором суммарные э. д. с. во всех контурах сохраняются неизменными, не влияет на токи в ветвях. Аналогично напряжения на ветвях определяются заданными величинами суммарных токов источников тока в узлах, и поэтому изменение расположения в схеме источников тока, при котором их суммарные токи во всех узлах сохраняются неизменными, не влияет на напряжения в схеме.

Если, например, требуется исключить источник э. д. с. из какой-либо ветви, то в данную ветвь вводится компен­сирующая э. д. с, причем точно такая же э. д. с. вво­дится одновременно во все остальные ветви, сходящиеся в одном из узлов данной ветви. Компенсирующая и дополнительные э. д. с. имеют одинаковое направление по отношению к рассматриваемому узлу. В результате этого источник э. д. с. из ветви исключается и появляются источники э. д. с. в других ветвях схемы. Суммарные э. д. с. во всех контурах и соответственно токи в ветвях остаются прежними.

Итак, источник э. д. с. может быть перенесен из ка­кой-либо ветви схемы во все другие ветви, присоединен­ные к узлу данной ветви, без изменения токов в схеме.

Рисунок 4-13. Перенос источников э.д.с. в схеме.

Справедливо и обратное положение: если во всех ветвях, кроме одной, сходящихся в узле, имеются оди­наковые источники э. д. с. (рисунок 4-13,а), направленные

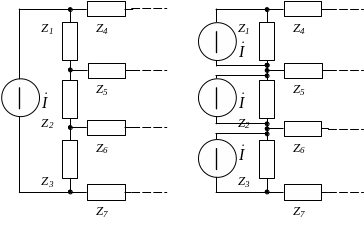
Рисунок 4-14. Перенос источников тока в схеме.

все к одному узлу или все от узла, то они мо­гут быть заменены од­ним источником э.д. с. в ветви, в которой ис­точник отсутствовал (рисунок 4-13,б).

Это положение под­тверждается тем, что суммарные э. д. с. в контурах схем на рисунок 4-13, а и б одинаковы.

Имеется и другое доказательство данно­го положения: ввиду равенства э. д. с. всех источников вторые зажимы их мо­гут быть объединены, как имеющие одинаковый потен­циал. В результате такого объединения, показанного на рисунке 4-13, а пунктиром, получается схема рисунок 4-13,б.

В случае переноса источников тока они присоединя­ются к узлам схемы так, чтобы оставались неизменными их суммарные токи в узлах. Так, например, несмотря на то, что источники тока размещены в схемах рисунок 4-14, а и б различно, суммарные токи источников в узлах обеих схем одинаковы. Поэтому и напряжения между уз­лами не изменились.

Итак, источник тока может быть заменен источника­ми тока, подключенными параллельно всем ветвям, ко­торые составляли контур с рассматриваемым источни­ком.

4-9. ПРЕОБРАЗОВАНИЕ СИММЕТРИЧНЫХ СХЕМ

Схема электрической цепи, в которой имеется ось симметрии, называется симметричной. Например, схема рисунок 4-16, а симметрична относительно вертикальной оси. В симметричных схемах легко выявляются точки или уз­лы с одинаковым потенциалом. В ветвях, присоединенных к таким узлам, токи равны нулю. Поэтому эти ветви можно разрезать, не нарушая распределения токов и на­пряжений в схеме. Точки, имеющие одинаковый потенциал, могут быть объединены.

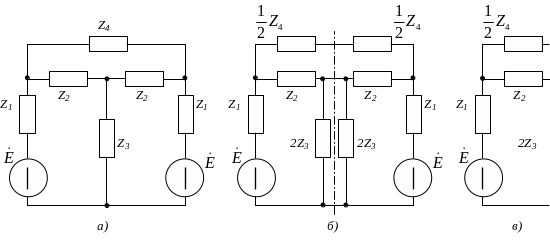
Рисунок 4-16. Симметричная цепь (а и б) и ее отсеченная половина (в).

Рассечение ветвей, по ко­торым не проходит ток, и объединение точек равного потенциала упрощают схему и облегчают расчет.

Рисунок 4-17. Симметричная цепь с неодинаковой полярностью источников (а) и ее закороченная половина (б).

Так, в симметричной схеме рисунок 4-16,б токи в соединениях, пересекающих ось симметрии, от­сутствуют. Разрезав схему по оси симметрии, получим с обеих сто­рон одноконтурную схему рисунок 4-16, в, которая легко рассчиты­вается.

Допустим теперь, что поляр­ность источников в симметричной схеме неодинакова (рисунок 4-17,а). В этом случае (равенство э. д. с. источников и различие их полярности) теки в симметричных вет­вях (например, и ) и напря­жения между соответствующими парами зажимов, симметрично расположенными относительно оси, равны по величине и проти­воположны по знаку. Отсюда сле­дует, что напряжения между всеми точками, лежащими на оси симметрии, равны нулю ( =-, т. е. =0). Поэтому все точки схемы на оси сим­метрии могут быть замкнуты накоротко (рисунок 4-17,б). Таким образом, расчет сложных симметричных схем приводится к расчету более простых схем.

Рисунок 4-18. Симметричная мостовая схема (а, б) и ее преобразованная часть

Рисунок. 4-19. Симметричная мостовая схема (а) и ее преобразованная часть (б)

На рисунок 4-18, а и б показана симметричная мостовая схема, имеющая две оси симметрии — вертикальную и горизонтальную. В продольных ветвях ток отсутствует; потенциалы средних точек поперечных (перекрещенных) ветвей одинаковы.

Поэтому продольные ветви могут быть рассечены, а средние точки поперечных ветвей — объединены. В ре­зультате с обеих сторон получится одноконтурная схема (рисунок 4-18,в), расчет которой крайне прост.

Если изменить полярность одного из источников (рисунок 4-19,а), то роли продольных и поперечных ветвей поме­няются и преобразованная часть схемы примет вид, по­казанный на рисунок 4-19,б.

В разобранных выше примерах э. д. с. источников были равны. В случае неравенства э. д. с. источников преобразование симметричной схемы удобно сочетается с методом наложения.

14