
336 Часть II. Детство
Между тем ребенок, возможно, интересовался внешним видом различных существующих упаковок, а не тем, что взрослый человек считает необходимым отвечать на вопрос «почему?».
Пространственные отношения — еще один комплекс понятий, которые ребенок начинает усваивать в дошкольные годы. Смысл таких слов, как «внутри», «снаружи», «близко», «далеко», «над», «под», «вверху» и «внизу», усваивается ребенком в процессе экспериментирования со своим собственным телом (Wei-kart, Rogers & Adcock, 1971). Дэвид Вейкарт и его коллеги предположили, что дети сначала усваивают то или иное понятие с помощью собственного тела (сами проползают под столом), а затем с помощью какого-либо предмета (провозят под столом игрушечный грузовик). Позже они начинают выделять это понятие на картинках («Смотри, корабль проплывает под мостом!») и выражать его словами.
В табл. 7.2 обобщаются основные характеристики дооперационального мышления.
Таблица 7.2 Избранные характеристики дооперационального мышления
Допонятийная стадия |
||
Анимизм |
Вера в то, что практически все движущиеся объекты — живые. |
Солнце, луну, машины, поезда ребенок считает живыми существами. |
Материализация |
Вера в то, что объекты и люди из фантазий и снов — реальны. |
Монстр из сна действительно скрывается под кроватью. |
Эгоцентризм |
Видение и осмысление вещей исключительно с собственной точки зрения. |
«Если я это вижу, ты должен тоже это видеть». |
Интуитивная стадия |
||
Символическая репрезентация |
Использование действий, образов или слов для представления (изображения) объектов и событий. |
Кубики изображают дома; названия представляют объекты. |
Социоцентрич-ное мышление |
Начало способности понимать точку зрения других. |
«Может, ты не хочешь играть в ту игру, в которую я хочу?» |
Ограничения дооперационального мышления |
||
Конкретность |
Неумение обращаться с абстракциями. |
Мышление ориентировано на «здесь и сейчас», а не на то, что могло бы быть. |
Необратимость |
Невозможность видеть обратимость изменений; одна из причин отсутствия понимания сохранения. |
«У меня есть брат, но у него нет братьев и сестер». |
Центрация |
Невозможность сконцентрироваться в один момент времени более чем на одном аспекте проблемы; еще одна причина отсутствия понятия сохранения. |
Мышление фокусируется на одном измерении объекта, упуская из виду другие. |
Инвариантность
В качестве свидетельства ограничений дооперационального мышления приводится отсутствие у детей инвариантности (понятия сохранения), на которое указывал Пиаже. Под термином сохранение имеется в виду осознание того, что изменение формы или внешнего вида материалов не приводит к изменению их объема, массы, количества. Ниже приведены примеры, подтверждающие это положение.
Инвариантность объема. Пиаже в ходе наблюдений определил, что дети с дооперациональным мышлением еще не владеют понятием сохранения объема, что подтверждается его классическим экспериментом «Жидкость и емкости» (рис. 7.4). Сначала ребенку показывают два одинаковых стакана, содержащих одинаковое количество жидкости. На вопрос: «Одинаковы ли они?» ребенок уверенно отвечает: «Да». Затем, прямо на глазах ребенка, содержимое одного из этих стаканов переливается в высокий узкий стакан. Экспериментатор спрашивает ребенка: «Одинаковые ли они?» Дети, находящиеся на дооперациональной стадии развития интеллекта, склонны отвечать, что они разные, и даже добавлять к этому, что в высоком стакане содержится больше жидкости. Очевидно, что здесь оказывает влияние такое свойство, как центрация; ребенок учитывает только одно измерение, а именно высоту, и не осознает, что за счет меньшей ширины стакана изменение высоты компенсируется. Для него эта проблема является проблемой перцептивного, а не логического характера, он просто фокусируется на ситуации «здесь и сейчас», и в результате состояние жидкостей до переливания является для него совсем другой задачей, чем после этой процедуры. Другими словами, с его точки зрения, переливание иррелевантно.
Необратимость также играет свою роль в отсутствии у ребенка понимания сохранения объема. Он считает, что невозможно перелить жидкость из высокого стакана обратно в первый и сохранить при этом тот же ее объем. Здесь также наблюдается неразвитость логического мышления.
И нвариантность
массы. На
рис. 7.5 представлены тесты, исследующие
осознание ребенком понятия сохранения
массы и демонстрирующие особенности
дооперационального мышления. В этом
случае наблюдается ситуация, схожая с
той, что мы видели в эксперименте с
жидкостью и стаканами. Ребенку показывают
два одинаковых шарика из пластилина.
На его глазах один шарик сминают и лепят
из
нвариантность
массы. На
рис. 7.5 представлены тесты, исследующие
осознание ребенком понятия сохранения
массы и демонстрирующие особенности
дооперационального мышления. В этом
случае наблюдается ситуация, схожая с
той, что мы видели в эксперименте с
жидкостью и стаканами. Ребенку показывают
два одинаковых шарика из пластилина.
На его глазах один шарик сминают и лепят
из
Рис. 7.4. Классический эксперимент «Жидкость и емкости», направленный на изучение понятия сохранения объема.
Р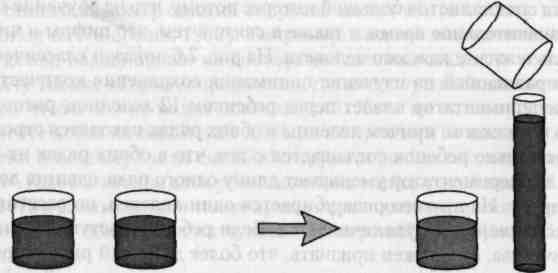 ис.
7.5. Эксперимент «Сохранение массы». В
эксперименте, направленном на изучение
понимания сохранения массы, ребенку
показывают два одинаковых шарика из
пластилина. Форма одного шарика остается
неизменной, в то время как другой шарик
претерпевает различные превращения
ис.
7.5. Эксперимент «Сохранение массы». В
эксперименте, направленном на изучение
понимания сохранения массы, ребенку
показывают два одинаковых шарика из
пластилина. Форма одного шарика остается
неизменной, в то время как другой шарик
претерпевает различные превращения
него фигуры различных форм, тогда как другой шарик остается в первоначальном виде. Рассмотрим пример, в котором шарик раскатывают и придают ему форму вытянутой сосиски. В силу центрации ребенок может сказать, что в сосиске больше пластилина либо что в ней меньше пластилина, в зависимости от того, к чему—к длине или к высоте — «прицепилось» его внимание. Как и в предыдущем эксперименте, ребенок, пойманный в ловушку «здесь и сейчас», не может осознать обратимость данного процесса.
Инвариантность количества и числа. Развитие у детей навыков счета представляет для специалистов большой интерес потому, что на обучение ему в школе отводится значительное время, а также в связи с тем, что цифры и числа играют важную роль в жизни каждого человека. На рис. 7.6 показан классический эксперимент, направленный на изучение понимания сохранения количества и числа. Сначала экспериментатор кладет перед ребенком 12 леденцов, расположив их в два ряда по 6 в каждом; причем леденцы в обоих рядах находятся строго один над другим. Как только ребенок соглашается с тем, что в обоих рядах их количество одинаково, экспериментатор уменьшает длину одного ряда, сдвигая леденцы ближе друг у другу. Из другого ряда убирается один леденец, но расстояние между оставшимися конфетами увеличивается. Если ребенку доступно понятие сохранения количества, он должен признать, что более длинный ряд состоит из меньшего количества леденцов, несмотря на свою протяженность. Детей в возрасте 5-6 лет обманчивый внешний вид длинного ряда часто вводит в заблуждение, и они говорят, что в нем больше леденцов.
Р ис.
7.6.
Эксперимент, направленный на изучение
понимания сохранения количества. Ребенку
4-5-лет показывают два ряда леденцов,
расположенных
ис.
7.6.
Эксперимент, направленный на изучение
понимания сохранения количества. Ребенку
4-5-лет показывают два ряда леденцов,
расположенных
в верхней части рисунка. Далее его спрашивают, в каком из них конфет больше. Дети, как правило, отвечают, что в обоих рядах одинаковое количество леденцов. Затем леденцы нижнего ряда сдвигают ближе друг к другу, а из верхнего убирают один, увеличивая при этом расстояние между оставшимися леденцами так, чтобы верхний ряд стал длиннее нижнего. Ребенок наблюдает за этой операцией, и ему говорят, что он может съесть леденец из того ряда, в котором их больше. Даже те дети, которые умеют считать, будут настаивать, что в длинном ряду леденцов больше, причем они будут делать это и после того, как сосчитают их количество в каждом ряду.
