Системы счисления, используемые в компьютере. Представление чисел в памяти ЭВМ.

• Системы счисления.

С древних времен человечество использует различные системы счета. Люди предпочитают десятичную систему, вероятно, потому, что считали по пальцам, а пальцев у людей по десять на руках и ногах. Не всегда и не везде люди пользуются десятичной системой счисления. В Китае, например, долгое время пользовались пятеричной системой счисления.

1	0	0	0	0	0	0	1	1
1	0	0	1	1	0	0	0	1

В процессах хранения, обработки и передачи различной информации в компьютере используется двоичная система счисления. Если «заглянуть» внутрь машинной памяти ее удобно представить в виде листа в клетку. В каждой такой «клетке» хранится только одно из двух значений: нуль или единица. Каждая «клетка» памяти компьютера называется битом. Цифры 0 и 1, хранящиеся в «клетках» памяти компьютера называют значениями битов. С помощью последовательности битов можно представить различную информацию. Такое представление информации называется цифровым или двоичным кодированием. Преимущество цифрового кодирования данных в том, что их можно хранить и передавать с использованием одних и тех методов, независимо от типов данных.

Двоичная система счисления (двоичное кодирование информации) имеет ряд преимуществ перед другими системами:

• для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток — нет тока, намагничен — не намагничен и т.п.), а не, например, с десятью, — как в десятичной;

• представление информации посредством только двух состояний надежно и помехоустойчиво;

• возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;

• двоичная арифметика намного проще десятичной.

Недостаток двоичной системы — быстрый рост числа разрядов, необходимых для записи чисел.

Система счисления — это совокупность приемов и правил, по которым числа записываются и читаются.

Позиционные и непозиционные системы счисления.

В непозиционных системах счисления вес цифры (т. е. тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа. Так, в римской системе счисления в числе ХХХII (тридцать два) вес цифры Х в любой позиции равен просто десяти.

В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число.

Например, в числе 757,7 первая семерка означает 7 сотен, вторая — 7 единиц, а третья — 7 десятых долей единицы.

Сама же запись числа 757,7₁₀ означает сокращенную запись выражения, которую можно разложит по позициям (разрядам): сотен, десятки, единицы и т.д. Нумерация разрядов целой части числа с право налево, от 0,1,2...

2 1 0 -1 разряды числа

757,7₁₀

700 + 50 + 7 + 0,7 = 7 *10² + 5 * 10¹ + 7*10⁰ + 7*10^—1 = 757,7.

Запись чисел в каждой из систем счисления с основанием q означает сокращенную запись выражения

a_n-1*q^n-1 + a_n-2*q^n-2 + ... + a₁*q¹ + a₀*q⁰ + a_-1*q^-1 + ... + a_-m*q^-m,

где:

a_i – цифры числа;

q – основание системы счисления;

n – число целых разрядов;

m – число дробных разрядов;

Например:

Разряды 3210 -1

Число 1011,1₂= 1*2³+0*2²+1*2¹+1*2⁰+1*2^-1

Разряды 210 -1

Число 276,5₈= 2*8²+7*8¹+6*8⁰+5*8^-1

Основание позиционной системы.

Основанием позиционной системы называется возводимое в степень целое число, которое равно количеству цифр, используемых для изображения чисел в данной системе (2¹, 2³, 2⁴).

Основание позиционной системы счисления - количество различных цифр, используемых для изображения чисел в данной системе счисления. Основание показывает также, во сколько раз изменяется количественное значение цифры при перемещении ее на соседнюю позицию.

Наименование системы счисления соответствует ее основанию (десятичная, двоичная, восьмеричная, шестнадцатеричная и так далее).

Система счисления	Алфавит цифр системы
десятичная	1 2, 3, 4, 5, 6, 7, 8, 9, 0
двоичная	0, 1
восьмеричная	1, 2, 3, 4, 5, 6, 7
шестнадцатеричная	1,2,3,4,5,6,7,8,9,A(10),B(11),C(12),D(13),E(14), F(15)

Для чисел, имеющих как целую, так и дробную части, перевод из одной системы счисления в другую, осуществляется отдельно для целой и дробной частей.

• Перевод чисел из одной системы счисления в другую.

Перевод целых чисел из десятичной системы в другие системы счисления.

Для перевода целого десятичного числа N в систему счисления с основанием q необходимо N разделить с остатком ("нацело") на q , записанное в той же десятичной системе. Затем неполное частное, полученное от такого деления, нужно снова разделить с остатком на q , и т.д., пока последнее полученное неполное частное не станет равным нулю. Представлением числа N в новой системе счисления будет последовательность остатков деления, изображенных одной q-ичной цифрой и записанных в порядке, обратном порядку их получения.

Пример:

Переведем число 75₁₀ из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

Ответ: 75₁₀ = 1 001 011₂ = 113₈ = 4B₁₆.

Перевод чисел из двоичной (восьмеpичной, шестнадцатеpичной) системы в десятичную.

Перевод в десятичную систему числа x, записанного в q-ичной cистеме счисления (q = 2, 8 или 16), сводится к вычислению значения многочлена:

x₁₀ = a_n*qⁿ + a_n-1* q^n-1 + .. + a₀* q⁰ + a_-1* q ^-1 + a_-2*q^-2 + ... + a_-m* q^-m

средствами десятичной арифметики.

Примеры:

Разряды 3210 -1

Число 1011,1₂= 1*2³+0*2²+1*2¹+1*2⁰+1*2^-1=8+0+2+1+0,5=11,5₁₀

Разряды 210 -1

Число 276,5₈= 2*8²+7*8¹+6*8⁰+5*8^-1=128+56+48+0,625=190,625₁₀

Разряды 210

Число 1F3₁₆= 1*16²+ 15*16¹+ 3*16⁰+ =256+240+3=499₁₀

2.Пеpевод пpавильных десятичных дpобей.

Для перевода правильной десятичной дроби F в систему счисления с основанием q необходимо F умножить на q , записанное в той же десятичной системе, затем дробную часть полученного произведения снова умножить на q, и т. д., до тех пор, пока дpобная часть очередного пpоизведения не станет pавной нулю, либо не будет достигнута требуемая точность изображения числа F в q-ичной системе. Представлением дробной части числа F в новой системе счисления будет последовательность целых частей полученных произведений, записанных в порядке их получения и изображенных одной q-ичной цифрой. Если требуемая точность перевода числа F составляет k знаков после запятой, то предельная абсолютная погрешность при этом равняется q ^-(k+1) / 2.

Пример.

Переведем число 0,36₁₀ из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

При умножении дроби на основание системы счисления q (2, 8, 16) в левой части остаются цифры алфавита этой системы счисления в (в двоичной – цифры 0,1 , в восьмеричной – цифры от 1 до 7, в шестнадцатеричной от 1 до 9,A-10,B-11,C-12.D-13,E-14,F-15).

Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему.

Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно в три (восьмеричная) и в четыре (шестнадцатеричная) раза меньше разрядов, чем в двоичной системе (ведь числа 8 и 16 — соответственно, 2³ и 2⁴).

Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр).

Например:

Перевод из двоичной системы счисления в восьмеричную или шестнадцатеричную.

Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на «триады» (для восьмеричной) или «тетрады» (для шестнадцатеричной)  и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой.

Например,

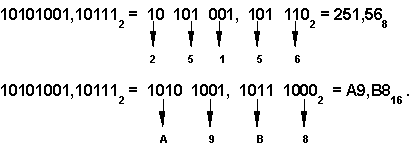
Сводная таблица переводов целых чисел.

• Арифметические действия над числами.

Рассмотрим основные арифметические операции: сложение, вычитание, умножение и деление. Правила выполнения этих операций в десятичной системе хорошо известны — это сложение, вычитание, умножение столбиком и деление углом. Эти правила применимы и ко всем другим позиционным системам счисления.

Сложение чисел в различных системах счисления.

Сложение проводится столбиком поразрядно, начиная с младшего нулевого разряда.

Если сумма двух чисел более основания системы(9₁₀+5₁₀=14₁₀> q=10), происходит переполнение нулевого разряда (14₁₀-10₁₀=4₁₀), тогда 4₁₀ остается в нулевом разряде, а 1 десяток суммируется с десятками (8+2+1=11>q=10).. 10 единиц переходят в виде 1в старший разряд числа.

Те же правила при сложении двоичных чисел (q=2 двоичное число, содержит цифры 0 и 1, нет 2). При сложении 1₂+1₂=0₂, т.к. в двоичной системе нет цифры 2, переполнение происходит, когда сумма чисел >2, в нулевом разряде пишем 0, две единицы нулевого разряда двоичного числа, суммируется в виде 1 с числами первого разряда (1₂+1₂+1₂=11₂) и т.д.

При сложении восьмеричных чисел, основание системы q=8, алфавит цифр числа от 0 до 7 (нет числа больше 7). Переполнение происходит, когда сумма чисел >8 (т.е.5₈+4₈=9₈), тогда из суммы вычитается основание (q=8), т.е. 9₈ – 8₈=1₈, а восемь единиц нулевого разряда, суммируется в виде 1 с числами первого разряда (7₈+3₈+1₈=11₈) и т.д.

При сложении шестнадцатеричных чисел, основание системы q=16, алфавит цифр числа от 0 до 9, A(10), B(11), C(12), D(13), E(14), F(15) (нет чисел больше 15). Переполнение происходит, когда сумма чисел >15, (т.е.7₁₆+F(15)₁₆=22₁₆), тогда из суммы вычитается основание (q=16), т.е. 22₁₆ – 16₁₆=6₁₆, а 16 единиц нулевого разряда, суммируется в виде 1 с числами первого разряда (2₁₆+1₁₆+1₁₆=4₁₆) и т.д.

Вычитание чисел в различных системах счисления.

Если при вычитании чисел приходиться занимать единицу старшего разряда, она равна количеству единиц основания системы (q=2, 8, 16).

Например: Вычтем единицу из чисел 100₂, 100₈ и 100₁₆.