
О формление графиков.
Каждый график выполняется на миллиметровой
бумаге, снабжается заголовком, содержащим
точное описание зависимости, показываемой нём, и вклеивается в отчёт.
д.) Основные правила приближенных вычислений.
Значащими цифрами называются все его цифры, кроме нуля, если он стоит в начале. Пример: 0,03010 – 4 значащие цифры.
Общее правило – при вычислении сумм, разностей, произведений, частных результат не должен содержать больше значащих цифр, чем наименее точное из слагаемых, сомножителей и т.д.
При вычислении
функций ограничиваются числом значащих
цифр аргумента. Если результат вычисления
является промежуточным и используется
в дальнейших вычислениях необходимо
сохранить в нем на одну значащую цифру
больше, чем это требуется предыдущим
правилом. Если в вычисляемое выражение
входят постоянные типа
![]() ,
,
![]() ,
константы приборов и т.п., следует для
них брать значащих цифр на одну больше,
чем в самом неточном из участвующих в
выражениях чисел. Это делается для
того, чтобы вычисления с постоянными
не вносили дополнительные ошибки.
,
константы приборов и т.п., следует для
них брать значащих цифр на одну больше,
чем в самом неточном из участвующих в
выражениях чисел. Это делается для
того, чтобы вычисления с постоянными
не вносили дополнительные ошибки.
Если это по каким-либо причинном невозможно (например, значения постоянной прибора недостаточно точно известны), то соответствующую константу в выражении для физической величины следует рассматривать на ровне с другими переменными и в окончательном выражение для физической величины будет входить в погрешность соответствующей константы.
Абсолютную
погрешность следует всегда выражать в
тех же единицах, что и саму измеряемую
величину. Например, L
= (1,572
![]() )м,
но не L
= 1,572
)м,
но не L
= 1,572![]() мм.
Число его погрешность всегда записывается
так, что бы их последние цифры принадлежали
к одному и тому же десятичному разряду.
Нельзя писать 24
мм.
Число его погрешность всегда записывается
так, что бы их последние цифры принадлежали
к одному и тому же десятичному разряду.
Нельзя писать 24![]() ,
или 21,62
,
или 21,62
![]() .
Правильная запись 24,0
или
21,6
.
Правильная запись 24,0
или
21,6![]() .
Нуль писать так же обязательно, как и
любую другую цифру:
.
Нуль писать так же обязательно, как и
любую другую цифру:
![]() ,
но не
,
но не
![]() .
.
Приближенные числа
рекомендуется представлять в нормальном
виде, для чего первая значащая цифра
записывается в разряде единиц, а остальные
– в разряде десятых, сотых и т.д. Например:
![]() м
= (3,56
м
= (3,56![]() 0,4)
нм
0,4)
нм
Вычисленные погрешности прямых и косвенных измерений должны округляться до одной значащей цифры, за исключением тех случаев, когда она равна 1 – в этом случае сохраняется две значащих цифры, причём вторая из них округляется до 5.
При записи констант и других заданных чисел часто применяется неявный способ указания их погрешностей: выписывая только надёжно известные значащие цифры числового значения, а ненадёжные отбрасываются с применение обычных правил округления. Например, запись L = 1,2 м читается как L = (1,20 0,05) м и т.д.
е.) Кинематика материальной точки.
Материальной точкой называется тело, размерами, структурой и внутренними движениями которого в данных условиях при описании движения можно пренебречь.
Системой отсчёта (СО) называется совокупность тела отсчёта, относительно которого рассматривается движение других тел, линеек и часов. Прежде чем говорить о движении и его описывать нужно выбрать СО.
Кинематика изучает геометрические формы и типы движений безотносительно к причинам их вызывающим. Все СО кинематически эквивалентны в смысле возможности выбрать любую из них для описания движения.
Геометрическим изображением СО является система координат (СК). В декартовой прямоугольной СК движение точки описывается заданием вектор-функций,
![]() (1.15)
(1.15)
выражающей зависимость радиус-вектора движущейся точки от времени. Задание вектор-функции (1.15) эквивалентно заданию 3-х функций описывающих зависимость от времени координат точки:
![]() (1.16)
(1.16)
Выражения (1.15) и
(1.16) называются кинематическим
законом движения точки.
Траекторией
точки в
данной СО называется кривая, описываемая
точкой при движении. Уравнение траектории
получается из (1.16), путём исключения
времени
![]() .
.
Вектором
перемещения
![]() за промежуток времени
за промежуток времени
![]() называется
вектор равный (рис.2)
называется
вектор равный (рис.2)
![]() ,
(1.17)
,
(1.17)
Путь
![]() ,
пройденный точкой за промежуток времени
,
пройденный точкой за промежуток времени![]() ,
определяется как длина дуги между
точками 1 и 2.
,
определяется как длина дуги между
точками 1 и 2.
![]() (1.18)
(1.18)
Вектором средней
скорости
![]() называется
величина (рис.2)
называется
величина (рис.2)
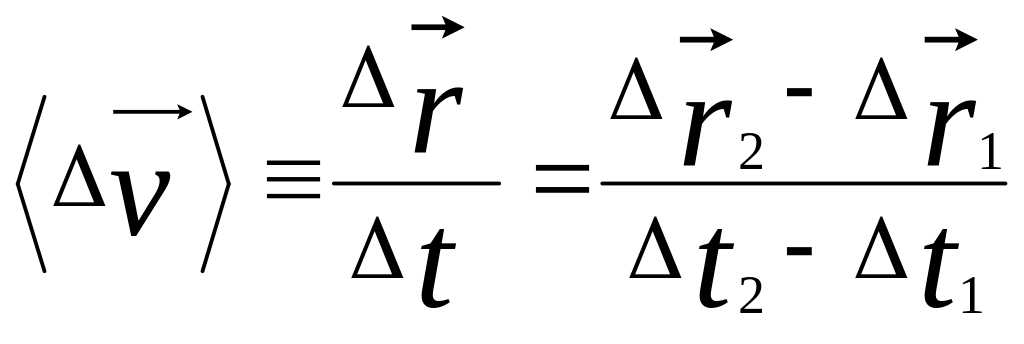 (1.19)
(1.19)
В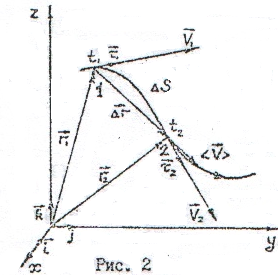 ектор
мгновенной скорости
ектор
мгновенной скорости
![]() характеризует быстроту измерения радиус
вектора точки в данный момент времени
и определяется равенством:
характеризует быстроту измерения радиус
вектора точки в данный момент времени
и определяется равенством:
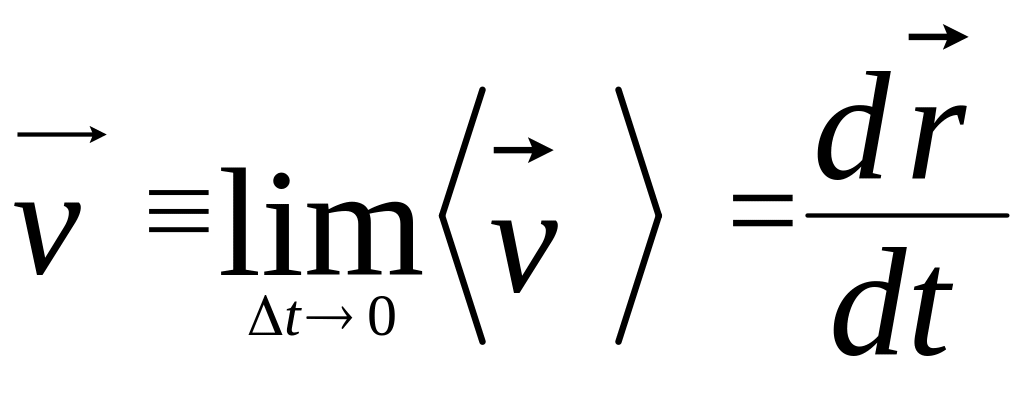 (1.20)
(1.20)
Проекции этого вектора на координатные оси равны:
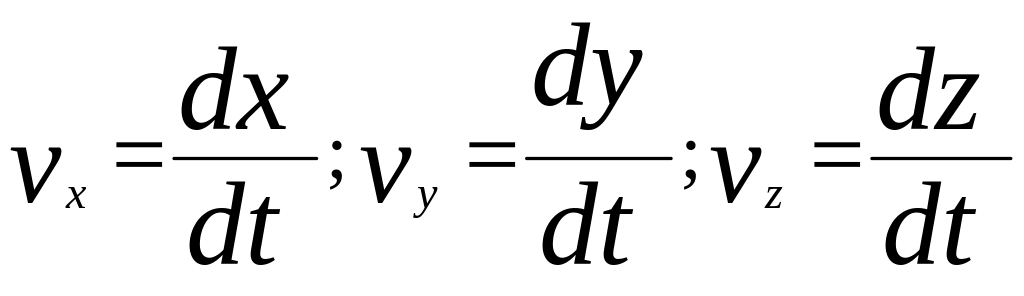 (1.20)
(1.20)
Тогда
![]() (1.21)
(1.21)
и модуль вектора скорости:
![]() (1.21)
(1.21)
Вектор
![]() направлен по касательной к траектории
в сторону движения точки (рис.2). Движение
точки можно задать и иначе:
задается уравнение траектории положение
точки на траектории в начальный момент
времени
направлен по касательной к траектории
в сторону движения точки (рис.2). Движение
точки можно задать и иначе:
задается уравнение траектории положение
точки на траектории в начальный момент
времени
![]() и зависимость пройденного пути от
времени
и зависимость пройденного пути от
времени![]() .
Такой способ задания движения принято
называть естественным.
Тогда модуль вектора скорости определяется
равенством:
.
Такой способ задания движения принято
называть естественным.
Тогда модуль вектора скорости определяется
равенством:
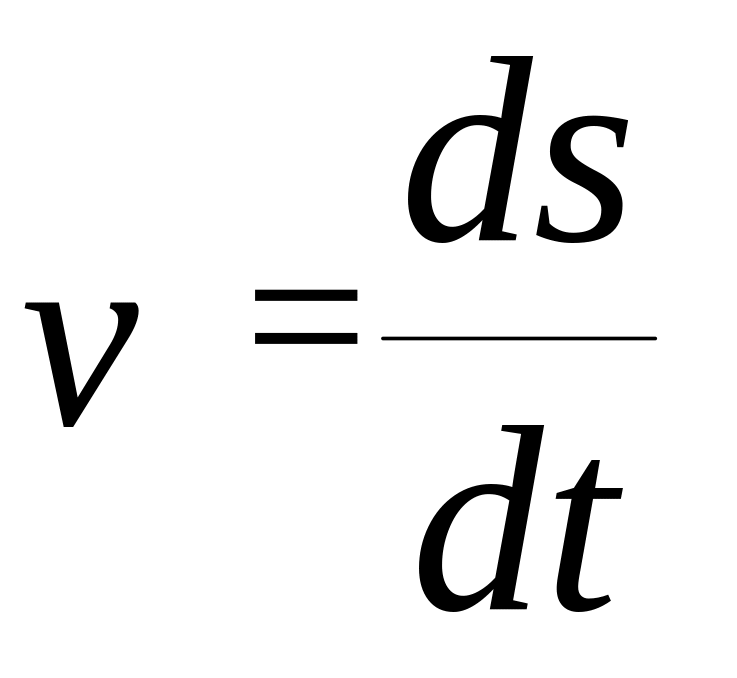 (1.22)
(1.22)
А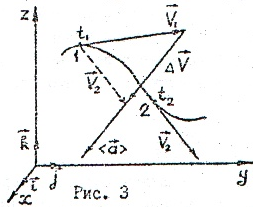 сам вектор записывается в виде:
сам вектор записывается в виде:
![]()
Где
![]() – единичный вектор касательной
– единичный вектор касательной
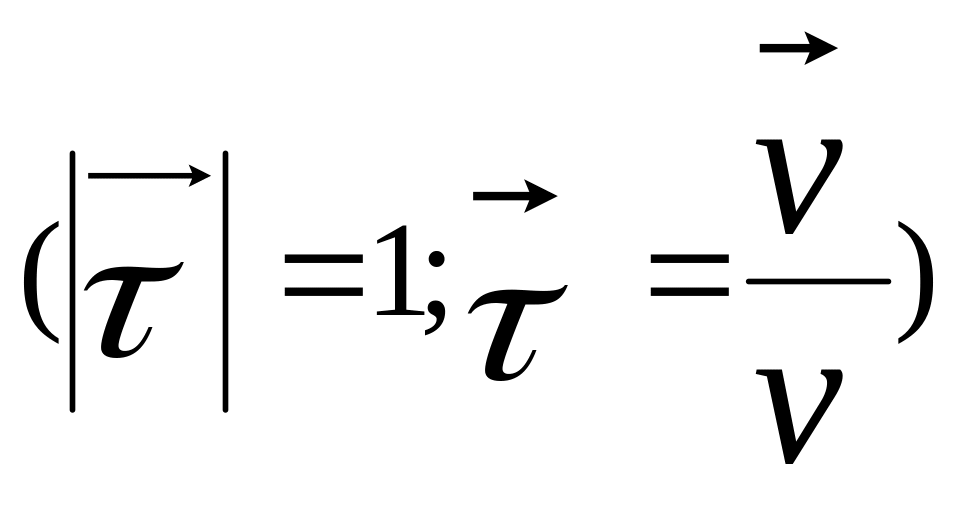 (1.23)
(1.23)
Направляющие косинусы векторы скорости :
![]()
![]() ;
;
![]() (1.24)
(1.24)
Вектор среднего
ускорения
![]() определяется равенством (рис.3)
определяется равенством (рис.3)
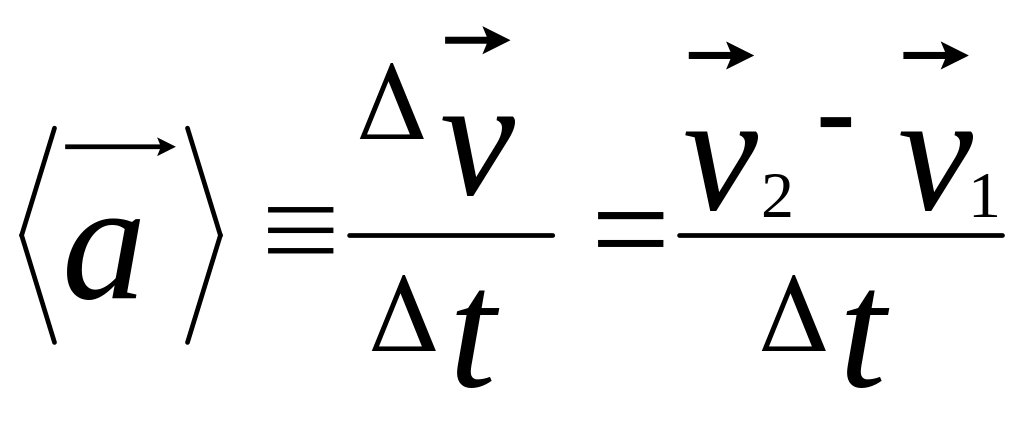 (1.25)
(1.25)
Вектором
мгновенного ускорения
![]() характеризует быстроту изменения
вектора скорости в данный момент и
определяется соотношением:
характеризует быстроту изменения
вектора скорости в данный момент и
определяется соотношением:
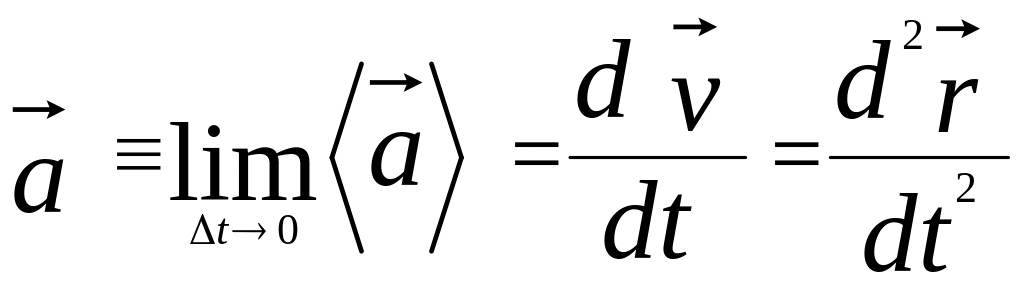 (1.26)
(1.26)
Проекции вектора ускорения на координатные оси:
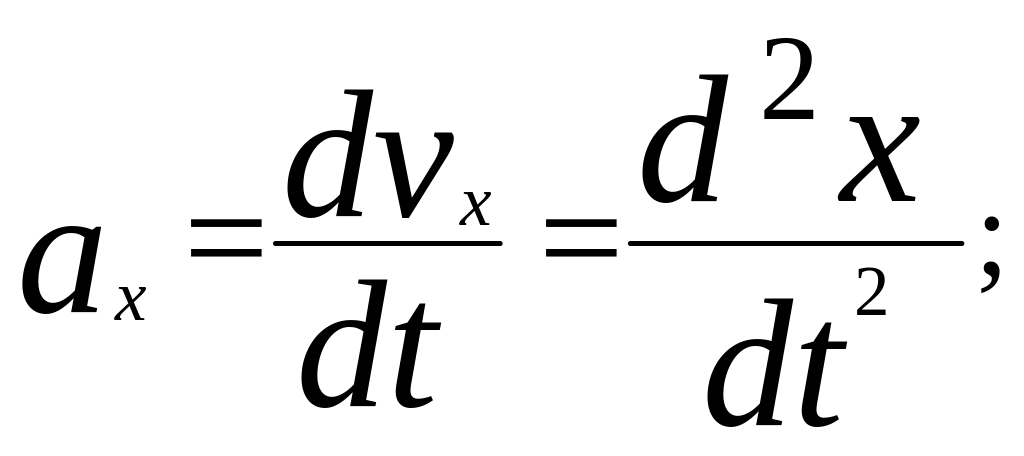
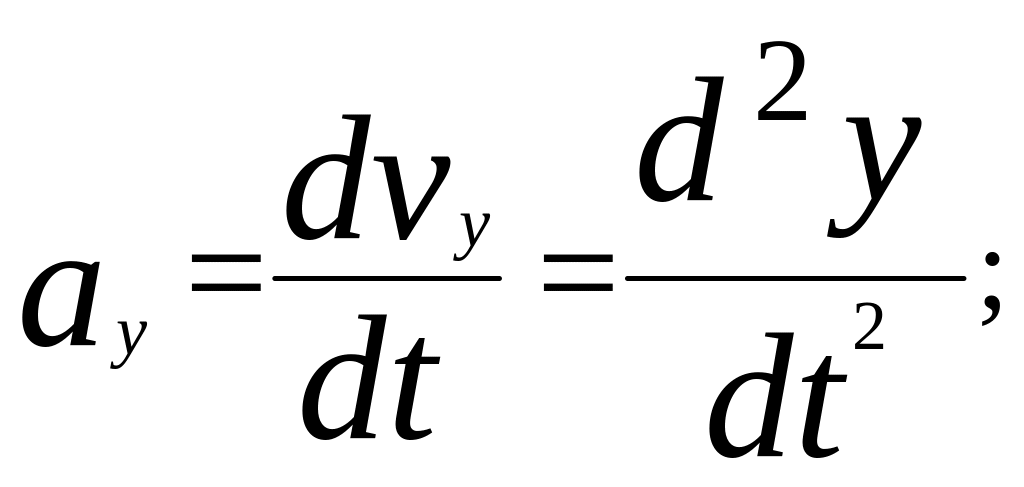
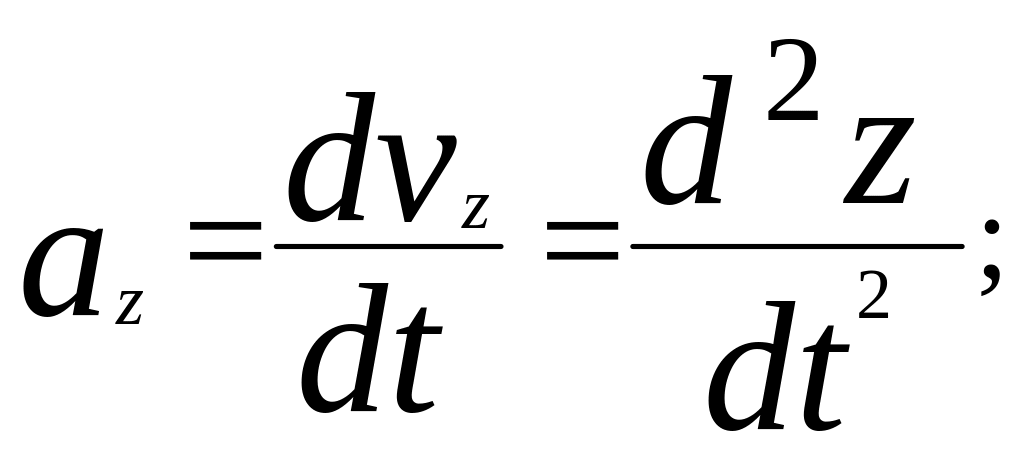
Тогда
![]()
И модуль вектора ускорения
![]()
Направляющие косинусы вектора ускорения
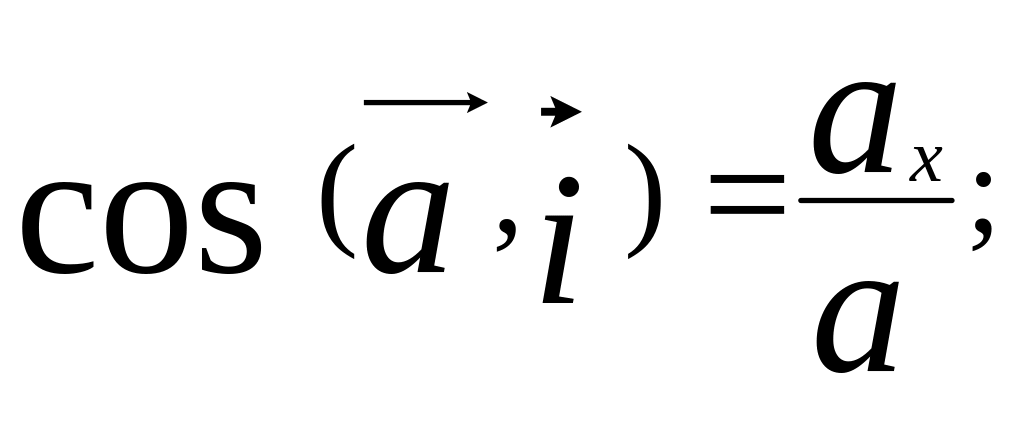
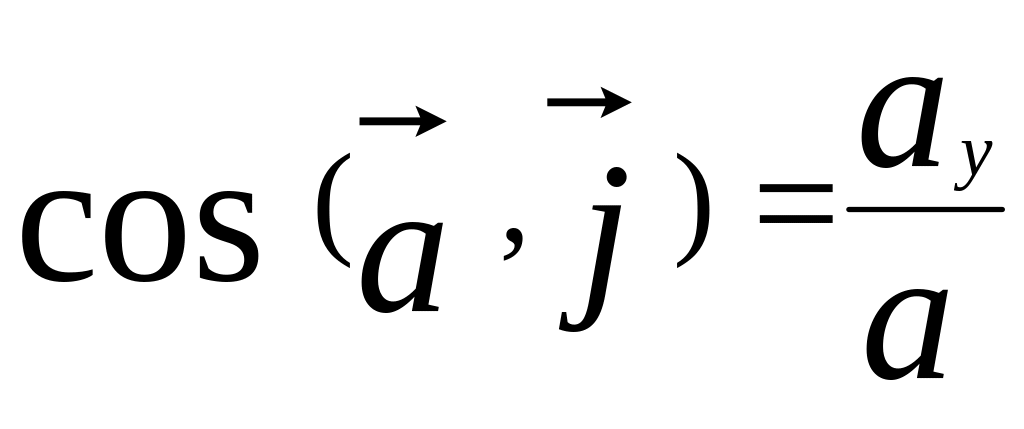 ;
;
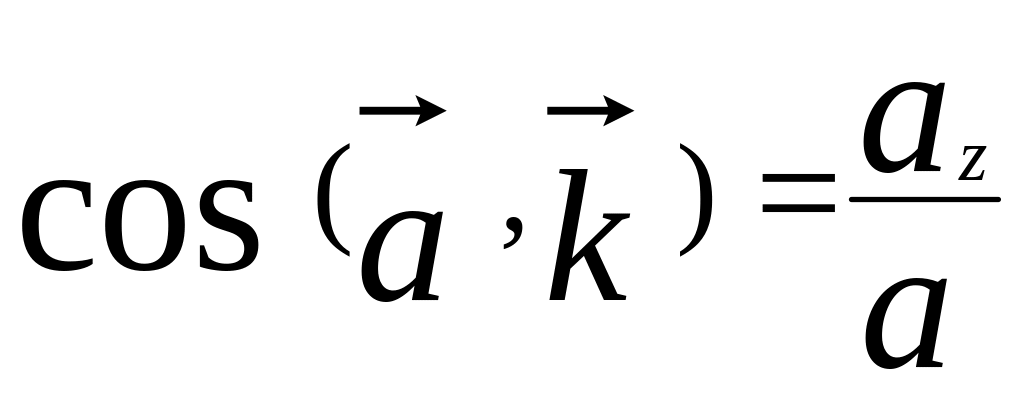
Угол между
векторами
![]() определяется из равенства
определяется из равенства
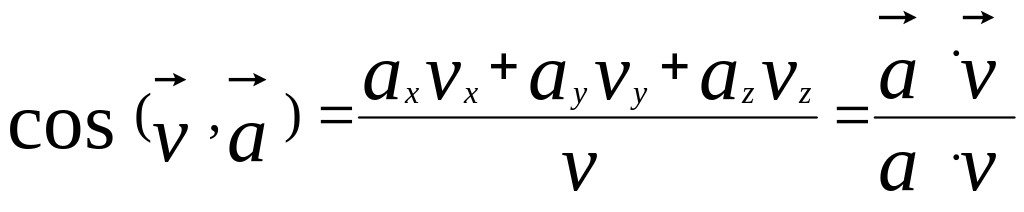
Тангенциальное
ускорение точки
![]() характеризует быстроту изменения
вектора скорости в данный момент
времени и выражается формулой
характеризует быстроту изменения
вектора скорости в данный момент
времени и выражается формулой
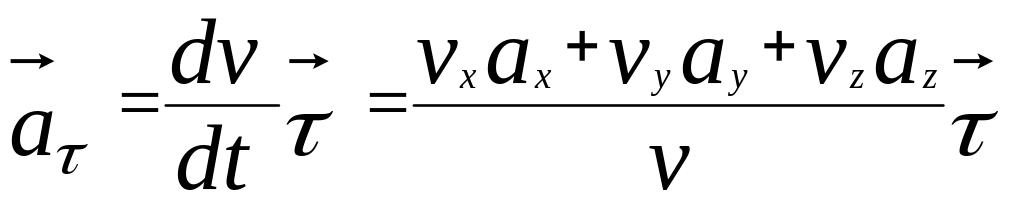
Где – единичный вектор касательной
Очевидно, имеет
место также равенство ![]()
Если
возрастает с течением времени, то
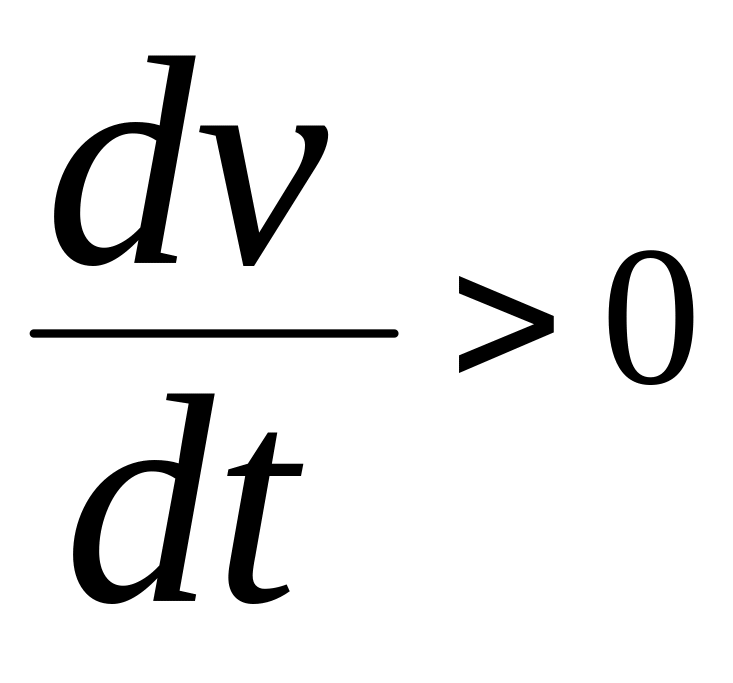 и
и
![]() т.е.
т.е.![]() - острый угол, если
убывает, то
и
- острый угол, если
убывает, то
и
![]() т.е - тупой угол (рис 4 )
т.е - тупой угол (рис 4 )
Н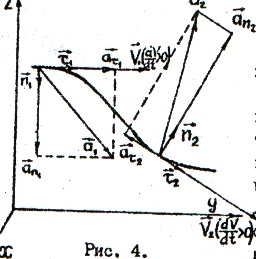 ормальное
ускорение
ормальное
ускорение
![]() характеризует быстроту изменения
характеризует быстроту изменения
в данный момент направления вектора и выражается формулой:

Где
![]() - единичный вектор нормали к траектории
направленный в сторону вогнутости
траектории
- единичный вектор нормали к траектории
направленный в сторону вогнутости
траектории
![]() - радиус кривизны траектории представляющий
собой радиус соприкасающейся с траекторией
в данной точке окружности совпадающей
с бесконечно малым элементом траектории,
с точностью до бесконечно малых второго
порядка малости
- радиус кривизны траектории представляющий
собой радиус соприкасающейся с траекторией
в данной точке окружности совпадающей
с бесконечно малым элементом траектории,
с точностью до бесконечно малых второго
порядка малости
Полное ускорение можно записать в виде
![]() и
и ![]()
Удобным способом нахождения всех кинематических характеристик движения точки является способ, основанный на использовании стробоскопических фотографий движущейся точки. Стробоскопические фотографии получаются если, если движущуюся точку фотографировать на один и то же кадр через строго фиксированные промежутки времени , называемые периодом стробоскопирования. Время открытия затвора должно быть малым для того, что бы за это время фотографируемая точка заметно не сдвинулась, и её изображение не смазалось. Применяется также вариант фотографирования в темноте с открытым затвором, а движущийся объект освещается короткими мощными импульсами света, следующими друг за другом за период времени , На фотографиях обычно указывается масштаб и период. Если движение точки происходит по пространственной кривой, то лучше как минимум две фотографии, снятые фотоаппаратами с разных позиций. Если движение происходит в плоскости, то фотоаппарат располагают так, что бы плоскости плёнки была параллельна этой плоскости. Можно считать при этом, что на фотографии в неискажённом виде в некотором масштабе получается картина движения точки. На фотографии со стрелкой указывается так же направление движения точки.
ж.) Пример определения кинематических характеристик по стробоскопическим фотографиям
На рисунке 5 приведена стробоскопическая фотография движения материальной точки и указаны координатные оси.
Задание 1. Найти кинематический закон движения точки.
Спроецируем точки
на координатные оси с учётом масштаба
и выпишем таблицу значений( табл.1)
координат точки, считая, что фотографирование
началось при
![]() измерения координат
и
прямы,
поэтому оценим их погрешности по методике
изложенной в пункте б). Поскольку в
данном случае нет особого смысла много
раз измерять координаты ибо мы будем
получать всё время один и то же результат
то следует предположить, что
измерения координат
и
прямы,
поэтому оценим их погрешности по методике
изложенной в пункте б). Поскольку в
данном случае нет особого смысла много
раз измерять координаты ибо мы будем
получать всё время один и то же результат
то следует предположить, что
![]() Это не значит, конечно что случайных
ошибок нет – просто они меньше точности
используемых инструментов. Приборная
погрешность при измерении стандартной
линейкой длинной 200 мм составляет
Это не значит, конечно что случайных
ошибок нет – просто они меньше точности
используемых инструментов. Приборная
погрешность при измерении стандартной
линейкой длинной 200 мм составляет
![]() мм. Погрешность счёта и округления при
округлении координат до 1 мм. составит
0.5 мм следует также учесть неидеальность
процедуры проектирования, которая так
же приводит к погрешности отсчёта и
округления и составляет примерно 0,5 мм
(подумайте, почему!) результирующая
погрешность с учётом масштаба будет
равна по формуле (1.10)
мм. Погрешность счёта и округления при
округлении координат до 1 мм. составит
0.5 мм следует также учесть неидеальность
процедуры проектирования, которая так
же приводит к погрешности отсчёта и
округления и составляет примерно 0,5 мм
(подумайте, почему!) результирующая
погрешность с учётом масштаба будет
равна по формуле (1.10)
![]()
(Множитель 10 за счёт масштаба)
П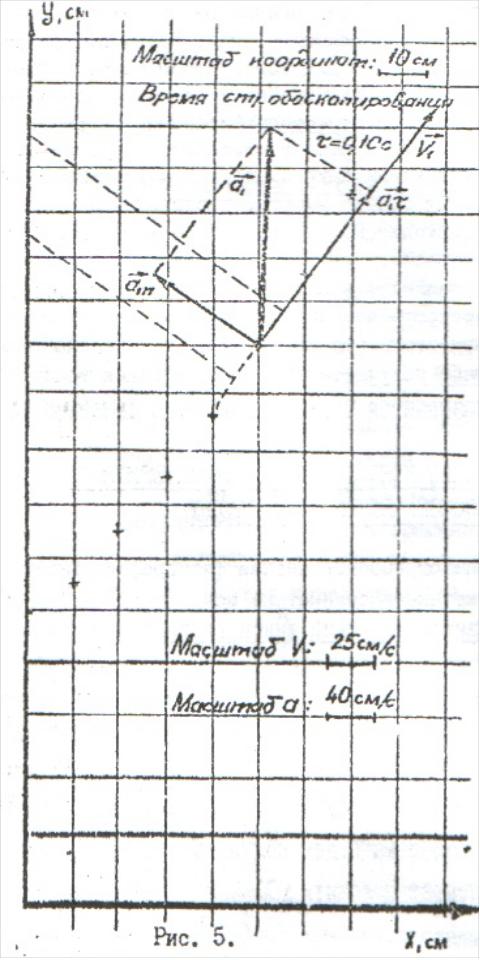 оскольку
отсчёты
и округлялись до целых сантиметров, то
следует положить
оскольку
отсчёты
и округлялись до целых сантиметров, то
следует положить![]() .
Для установления вида функциональной
зависимости
.
Для установления вида функциональной
зависимости
![]() изобразим данные табл. 1 на рисунке 6
откладывая время
по горизонтали, координату
по вертикали. ( в том же масштабе, что и
на рисунке 5, руководствуясь при этом
правилами изложенными в пункте д). (рис
6)
изобразим данные табл. 1 на рисунке 6
откладывая время
по горизонтали, координату
по вертикали. ( в том же масштабе, что и
на рисунке 5, руководствуясь при этом
правилами изложенными в пункте д). (рис
6)
При этом учитываем,
что погрешность
![]() задана неявно ( она равна 0,005 с) из
рисункам6 сразу видно, что искомая
функциональная зависимость
задана неявно ( она равна 0,005 с) из
рисункам6 сразу видно, что искомая
функциональная зависимость
линейная. Задача, следовательно состоит в том, чтобы провести по точкам рис.6 прямую, наилучшим в некотором смысле образом соответствующую этим точкам. Можно, конечно это сделать графически, однако это не даёт полной уверенности, что прямая - наилучшая.
t, c |
0 |
0,10 |
0,20 |
0,30 |
0,40 |
0,50 |
0,60 |
0,70 |
0,80 |
0,90 |
1,00 |
x, см |
0 |
11 |
19 |
29 |
41 |
51 |
59 |
71 |
79 |
91 |
100 |
y, см |
50 |
57 |
64 |
74 |
85 |
100 |
116 |
134 |
153 |
176 |
200 |
Одним из способов аналитического решения задачи о нахождении наилучшей прямой, соответствующей экспериментальным точкам, является метод наименьших квадратов.
И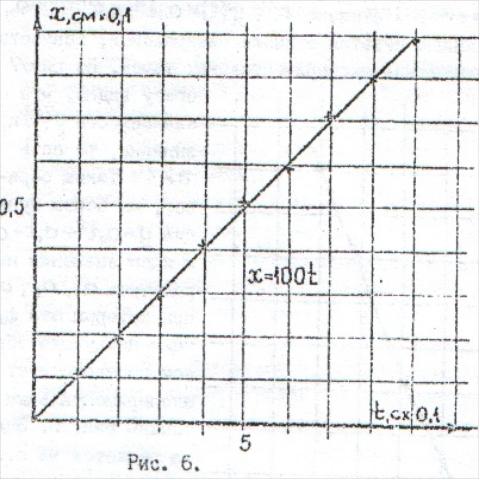 дея
метода состоит в следующем. Пусть
уравнение искомой прямой имеет вид
дея
метода состоит в следующем. Пусть
уравнение искомой прямой имеет вид
![]() ,
где
,
где
![]() и
и
![]() –постоянные подлежащие определению
при каждом значении времени
–постоянные подлежащие определению
при каждом значении времени![]() (0.1…10)
найдём величину
(0.1…10)
найдём величину
![]() представляющую квадрат разности между
экспериментальным значением величины
представляющую квадрат разности между
экспериментальным значением величины
![]() и значением
и значением
![]() ,
вычисленным по формуле, выражающей
ожидаемую линейную зависимость. Образуем,
далее, сумму
,
вычисленным по формуле, выражающей
ожидаемую линейную зависимость. Образуем,
далее, сумму
![]() .
Прямая
будет соответствовать экспериментальным
точкам наилучшим образом, если мы найдём
такие значения
и
,
при которых достигается минимуму суммы
.
Прямая
будет соответствовать экспериментальным
точкам наилучшим образом, если мы найдём
такие значения
и
,
при которых достигается минимуму суммы
![]() .
Условия минимума имеет вид
.
Условия минимума имеет вид
 ,
что даёт систему уравнений
,
что даёт систему уравнений
![]() и
и
![]() .
подставляя численные значения, получим
(выражаем
в см.):
.
подставляя численные значения, получим
(выражаем
в см.):
![]() и
и
![]()
Решая систему и
округляя значения
и
до трёх значащих цифр( с такой точностью
заданы
и
), получим
![]() ,
,
![]() .
.
Таким образом, искомая зависимость имеет вид.
![]() (см) (1.36)
(см) (1.36)
Для нахождения
вида функциональной зависимости
![]() поступим, аналогично изобразив данные
табл.1 на координатной плоскости
поступим, аналогично изобразив данные
табл.1 на координатной плоскости![]() (рис.7).
(рис.7).
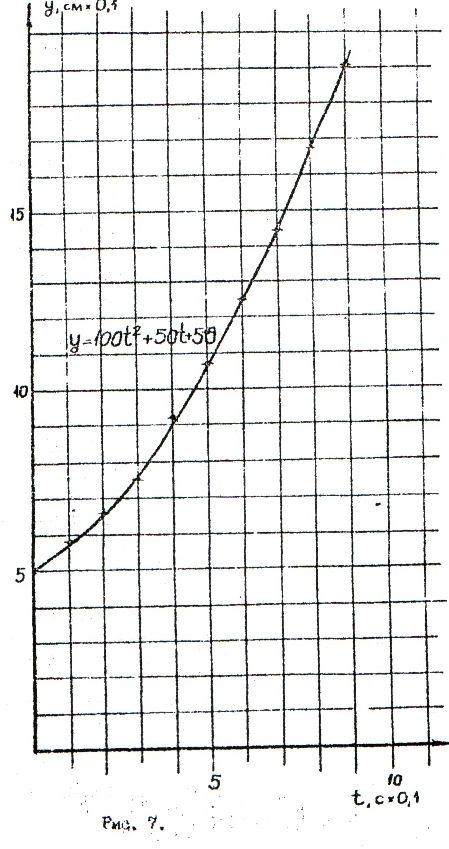 Из
рис.7 не вытекает, однако, с определённостью
предположение о виде зависимости
Из
рис.7 не вытекает, однако, с определённостью
предположение о виде зависимости
![]() .
В таких случаях обычно выдвигаются
гипотезы о том, какому классу функций
(полиномов, показательных, тригонометрических
и т.д.) принадлежит искомая зависимость,
а за тем эти гипотезы принимаются или
отвергаются. Чаще всего выдвигается
гипотеза о принадлежности неизвестной
функции
к классу полиномов некоторой степени
.
В таких случаях обычно выдвигаются
гипотезы о том, какому классу функций
(полиномов, показательных, тригонометрических
и т.д.) принадлежит искомая зависимость,
а за тем эти гипотезы принимаются или
отвергаются. Чаще всего выдвигается
гипотеза о принадлежности неизвестной
функции
к классу полиномов некоторой степени
![]()
Степень
![]() полинома обычно берется в начале
минимальной, совместной характером
расположения экспериментальных точек.
Из рис.7
полинома обычно берется в начале
минимальной, совместной характером
расположения экспериментальных точек.
Из рис.7
сразу видно, что
зависимость
не линейная, то есть
![]() .
Таким образом, мы берём функцию
.
Таким образом, мы берём функцию
![]() и ищем значения параметров
и ищем значения параметров
![]() ,
,![]() ,
,![]() ,
при которых эта функция наилучшим
образом соответствует экспериментальным
точкам рис.6. Задача решается на основе
метода наименьших квадратов. Условия
минимума суммы
,
при которых эта функция наилучшим
образом соответствует экспериментальным
точкам рис.6. Задача решается на основе
метода наименьших квадратов. Условия
минимума суммы
![]() дают
,
дают
,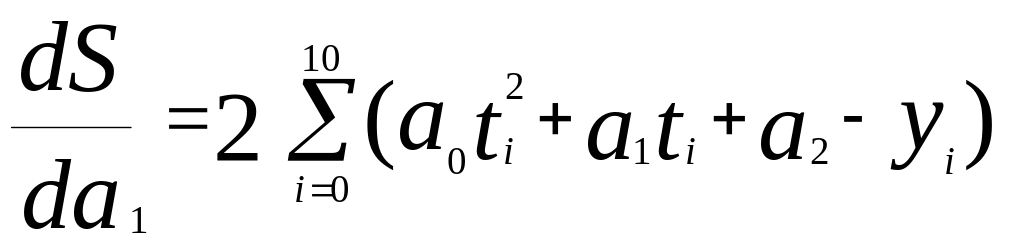
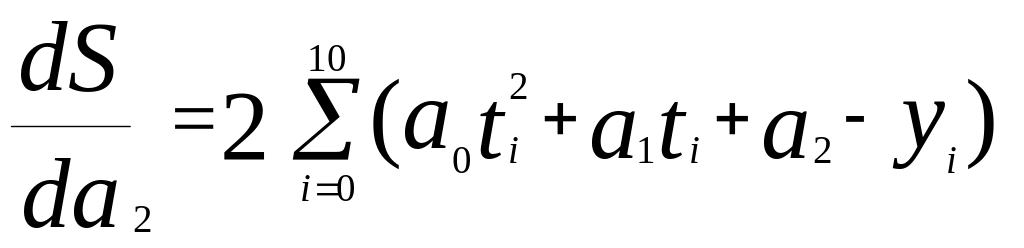 .
Подставляя численные значения и решая
систему уравнений, находим после
округления
.
Подставляя численные значения и решая
систему уравнений, находим после
округления
![]() ,
,![]() ,
,
![]() .
Таким образом
.
Таким образом![]() (1.37), Следует, однако, помнить, что
предположение о полиноминальной
зависимости
является лишь гипотезой. Ведь вполне
возможно, что функция вида
(1.37), Следует, однако, помнить, что
предположение о полиноминальной
зависимости
является лишь гипотезой. Ведь вполне
возможно, что функция вида
![]() ,
где постоянный подобраны с помощью
метода наименьших квадратов, и полином
степени большей 2 значительно лучше
соответствует экспериментальным точкам
рис.7. Иными словам. возникает вопрос.
насколько оправдана гипотеза о
полиноминальной зависимости степени
2 то есть насколько функция (1.37)
соответствует экспериментальным точкам.
,
где постоянный подобраны с помощью
метода наименьших квадратов, и полином
степени большей 2 значительно лучше
соответствует экспериментальным точкам
рис.7. Иными словам. возникает вопрос.
насколько оправдана гипотеза о
полиноминальной зависимости степени
2 то есть насколько функция (1.37)
соответствует экспериментальным точкам.
На первый взгляд
естественным представляется следующий
путь. с помощью метода наименьших
квадратов определим значения
,
,
![]() для функции вида
для функции вида
![]() ,
при которых она наилучшим образом
соответствует экспериментальным точкам
затем для этих значений
,
,
вычислим сумму квадратов разностей,
фигурирующих в методе, наименьших
квадратов, и сравним её с суммой для
полиноминальной зависимости (1.37).
Естетсвен6но, что та зависимость, для
которой это сумма меньше, лучше отвечает
экспериментальным точкам. Ясно, однако,
что этот путь хотя и возможен, но трудоёмок
и малоперспективен, поскольку существует
множество функций времени. которые
могли бы, принципе, соответствовать
экспериментальным точкам рисунка 5,
например, зависимость
,
при которых она наилучшим образом
соответствует экспериментальным точкам
затем для этих значений
,
,
вычислим сумму квадратов разностей,
фигурирующих в методе, наименьших
квадратов, и сравним её с суммой для
полиноминальной зависимости (1.37).
Естетсвен6но, что та зависимость, для
которой это сумма меньше, лучше отвечает
экспериментальным точкам. Ясно, однако,
что этот путь хотя и возможен, но трудоёмок
и малоперспективен, поскольку существует
множество функций времени. которые
могли бы, принципе, соответствовать
экспериментальным точкам рисунка 5,
например, зависимость
![]() с надлежаще подобранными константами
с надлежаще подобранными константами![]() .
Поэтому вопросы совместимости гипотезы
о той или иной зависимости ( в нашем
случае зависимости 1.37) с экспериментальными
данными решаются с помощью так называемых
критериев
согласия
(другое название – критерии
значимости
). Одним из наиболее удобных критериев
является так называемый «критерий
.
Поэтому вопросы совместимости гипотезы
о той или иной зависимости ( в нашем
случае зависимости 1.37) с экспериментальными
данными решаются с помощью так называемых
критериев
согласия
(другое название – критерии
значимости
). Одним из наиболее удобных критериев
является так называемый «критерий
![]() »
(читается хи-квадрат) или критерий
Пирсона.
»
(читается хи-квадрат) или критерий
Пирсона.
В методе вычисляется величина
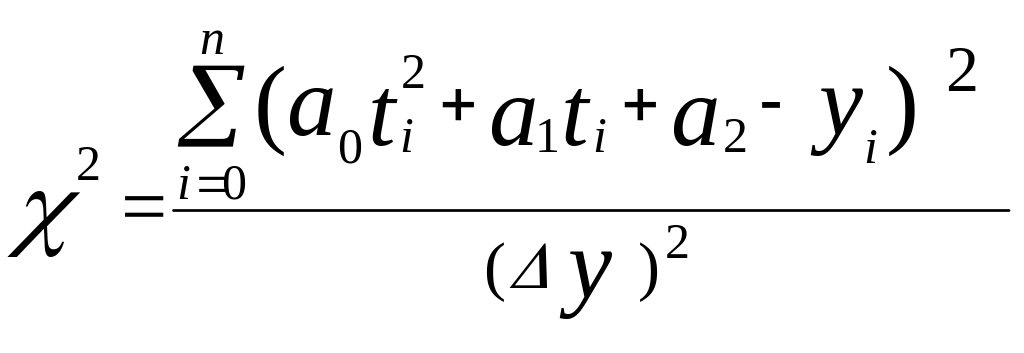 (1.38)
(1.38)
При найденных
методом наименьших квадратов значениях
,
,
,
то есть сумма квадратов отклонений
экспериментальных значений
![]() от вычисленных по формуле (1.37), деленная
на квадрат погрешности измерения
величины
.
В нашем случае
от вычисленных по формуле (1.37), деленная
на квадрат погрешности измерения
величины
.
В нашем случае
![]() .
Найденное значение должно быть
сопоставлено с теорией. Это делается с
помощью таблицы распределения
,
фрагмент которой приведён в табл.2. В
данной таблице
– это число степеней свободы распределения
,
равной числу измерений минус увеличенное
на единицу число параметров, определяемых
из эксперимента. В нашем случае число
измерений равно 11 и с помощью метода
наименьших квадратов было определено
3 параметра, так что
.
Найденное значение должно быть
сопоставлено с теорией. Это делается с
помощью таблицы распределения
,
фрагмент которой приведён в табл.2. В
данной таблице
– это число степеней свободы распределения
,
равной числу измерений минус увеличенное
на единицу число параметров, определяемых
из эксперимента. В нашем случае число
измерений равно 11 и с помощью метода
наименьших квадратов было определено
3 параметра, так что
![]() .
Число Р в таблице – вероятность,
выражаемая в процентах. По найденному
значению
и числу степеней свободы
.
Число Р в таблице – вероятность,
выражаемая в процентах. По найденному
значению
и числу степеней свободы
![]() находим,
что
находим,
что
![]() .
Это означает, что если гипотеза о
зависимости (1.37) справедлива, то найденное
значение должно встречаться примерно
в 88 % случаев или, иначе, с вероятностью
0,88 величина
будет превышать значение 3,0. Следовательно,
на уровне не доверительной вероятности
88% мы подтвердили зависимость (1.37). Если,
например, при тех же условиях
.
Это означает, что если гипотеза о
зависимости (1.37) справедлива, то найденное
значение должно встречаться примерно
в 88 % случаев или, иначе, с вероятностью
0,88 величина
будет превышать значение 3,0. Следовательно,
на уровне не доверительной вероятности
88% мы подтвердили зависимость (1.37). Если,
например, при тех же условиях
![]() ,
то это означало бы, что при справедливости
гипотезы (1.37) такие большие отклонения
встречались бы лишь в 5% случаев, так
что наше найденное значение
,
свидетельствовало о надёжности гипотезы
и это заставило бы искать другую
зависимость
,
например. в виде полинома третьей степени
и т.д.
,
то это означало бы, что при справедливости
гипотезы (1.37) такие большие отклонения
встречались бы лишь в 5% случаев, так
что наше найденное значение
,
свидетельствовало о надёжности гипотезы
и это заставило бы искать другую
зависимость
,
например. в виде полинома третьей степени
и т.д.
Выпишем окончательно найденный кинематический закон движения:
![]() (cм)
(см)
(cм)
(см)
На рис.6 и 7 построены для наглядности графики зависимостей (1.39)
Задание 2. Найти модуль скорости точки в середине интервала наблюдение и углы составляемые вектором скорости с осями координат в этот момент. Изобразить вектор скорости на рис.5 .
Середина интервала
наблюдения соответствует
![]() с.
с.
используя формулы (1.20;1.21) и (1.24) получим:
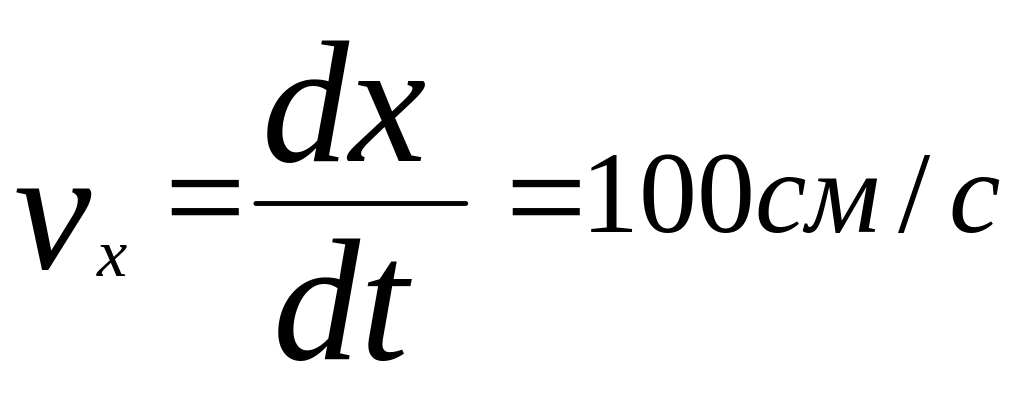
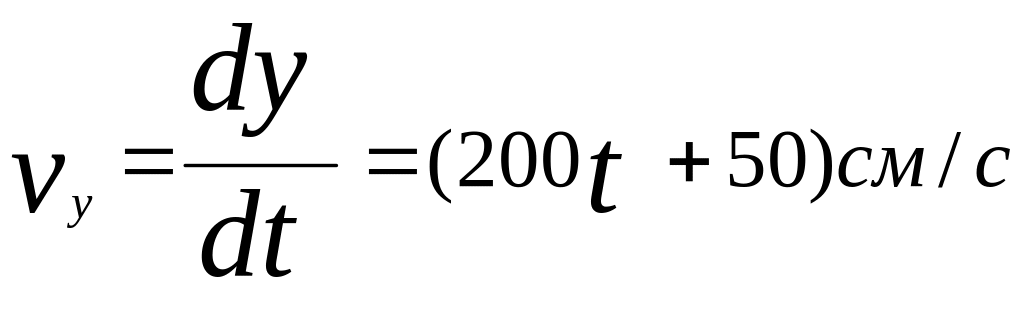
![]()
Полагая, что
![]() получим
получим
![]()
![]()
Рассчитаем
погрешности. Погрешность
![]() задаётся формой записи:
задаётся формой записи:
![]() для
нахождения
для
нахождения
![]() перепишем
перепишем
![]() в виде
в виде
![]()
![]() ,
где
,
где
![]() = 100
= 100
![]() ,
,![]()
![]() ,
,![]() ,
тогда используя формулу (1.13) получим:
,
тогда используя формулу (1.13) получим:
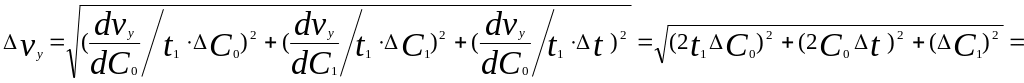
![]()
Таким образом, следует писать.
![]()
![]()
Аналогично
рассчитываются погрешности
![]() как косвенных физических величин.
Изображаем в подходящем масштабе на
рис.5 вектор.
как косвенных физических величин.
Изображаем в подходящем масштабе на
рис.5 вектор.
Задание 3. Найти ускорение точки в тот же момент времени и углы, составляемые вектором ускорения, с осями координат. Изобразить вектор ускорения на рис.5.
Используя формулы(1.27; 1.30) находим
 ;
; 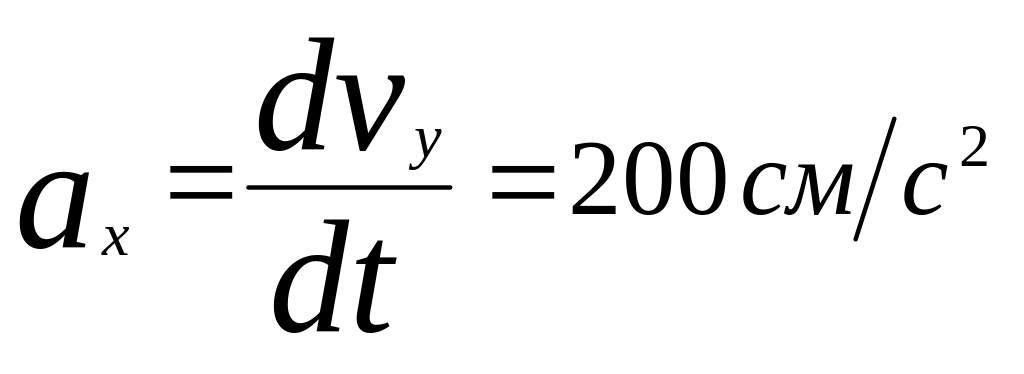 ;
; ![]()
Поскольку же
величины от времени не зависят, такими
же они и будут, и при
![]() .
Их погрешности задаются формой записи.
Изображаем в подходящем масштабе вектор
.
Их погрешности задаются формой записи.
Изображаем в подходящем масштабе вектор
![]() на чертеже.
на чертеже.
Далее: 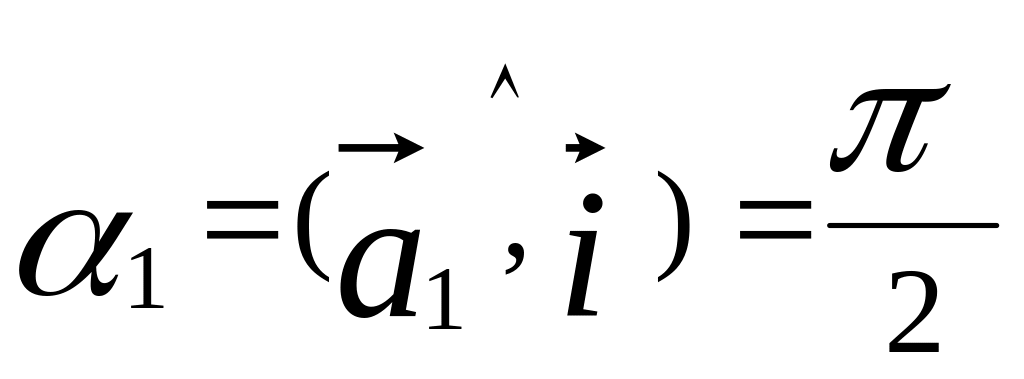
![]()
Задание
4. Найти тангенциальное и нормальное
ускорения точки в тот же момент времени.
Показать на рис.5 векторы.
![]() и
и![]()
Используя формулу (1.32) и вышеполученные результаты запишите.
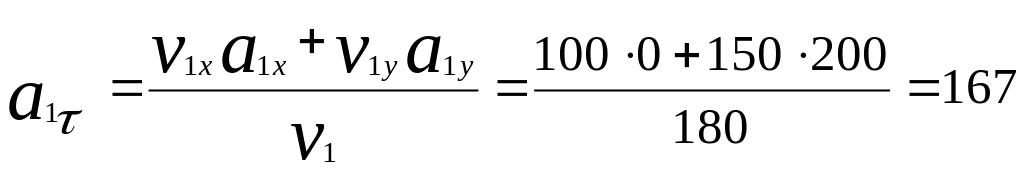
![]()
Направлен вектор
так же как и
![]() .
Изображаем его на чертеже. Вектор
может быть найден геометрически как
разность
и
(формула (1.35)):
.
Изображаем его на чертеже. Вектор
может быть найден геометрически как
разность
и
(формула (1.35)):
Правильность его
нахождении по чертежу на рис.5 можно
проконтролировать вычисляя его модуль: ![]()
Задание 5. Найти радиус кривизны траектории в точке, соответствующей тому же момент времени.
Используя формулу(1.34), находим:
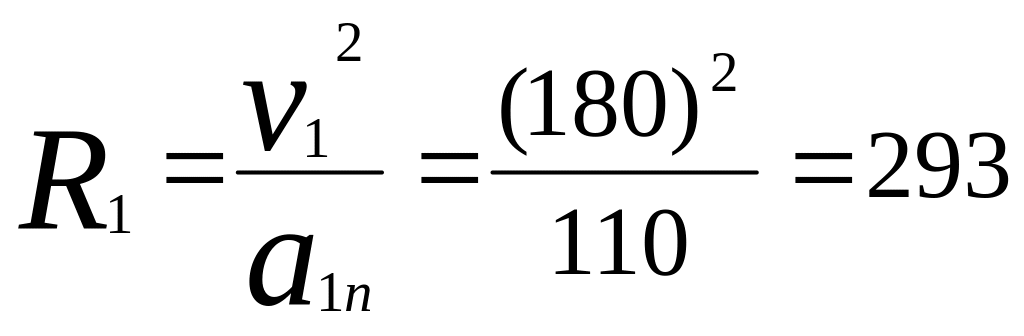 см
см
Расчёт погрешностей
в заданиях 4 и 5 проводится, так же как и
в задании 2. во многих случаях оказывается
полезным приближенный графический
способ нахождения радиуса кривизны.
Для этого точку на траектории,
соответствующую моменту времени
,
соединим прямолинейными отрезкам с
соседними точками, соответствующими
моментам![]() и
и![]() . Из середины этих отрезков восстанавливаем
перпендикуляр до их пересечения в точке
0.
. Из середины этих отрезков восстанавливаем
перпендикуляр до их пересечения в точке
0.
Точка 0 примерно
совпадает с центом соприкасающейся
окружности соответствующей участку
траектории вблизи точки, для которой
велось построение. Радиус этой окружности
примерно равен
![]() (на рис.5 точка 0 находится за пределами
листа бумаги).
(на рис.5 точка 0 находится за пределами
листа бумаги).
Задание 6. Найти зависимость пройденного пути S от времени t, то есть функцию S=S(t).
Задание 7. Найти среднюю скорость и ускорение за весь интервал наблюдения.
Задание 8. Написать уравнение траектории точки.
Методику вычисления заданий 6, 7, 8 студентам предлагается разработать самостоятельно.
Стробоскопические фотографии для выполнения работы каждый студент получает у преподавателя.
Контрольные вопросы.
Какие ошибки (пункт а)) имели место при выполнении работы и как они учитывались?
Как изменилась точность ваших результатов, если бы вы проводили все измерения и построения несколько раз, используя разные инструменты?
Как можно проверить отсутствие промахов в серии наблюдений?
Изложите методику расчёта погрешностей при измерении объёма цилиндра штангенциркулем.
Нарисуйте, примерно, как будет выглядеть стробоскопическая фотография движения точки при
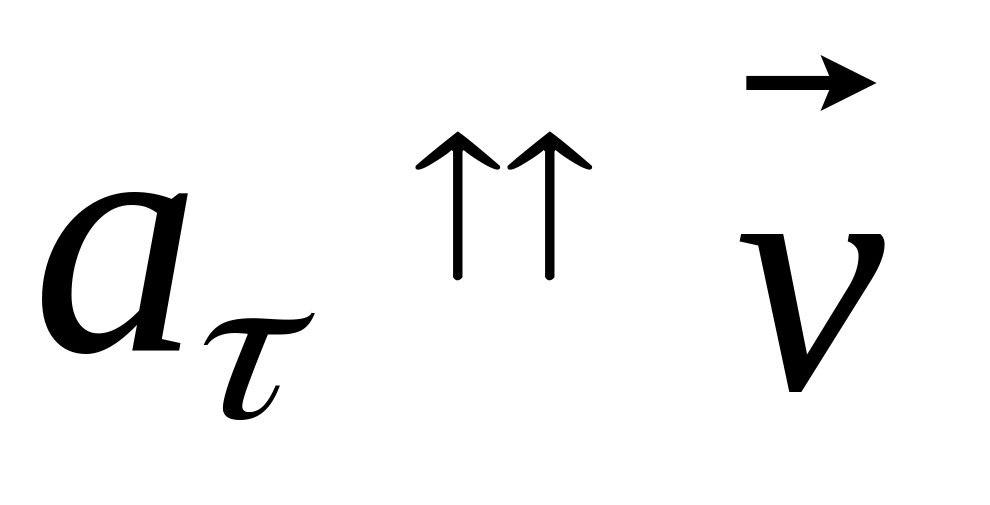 и
и
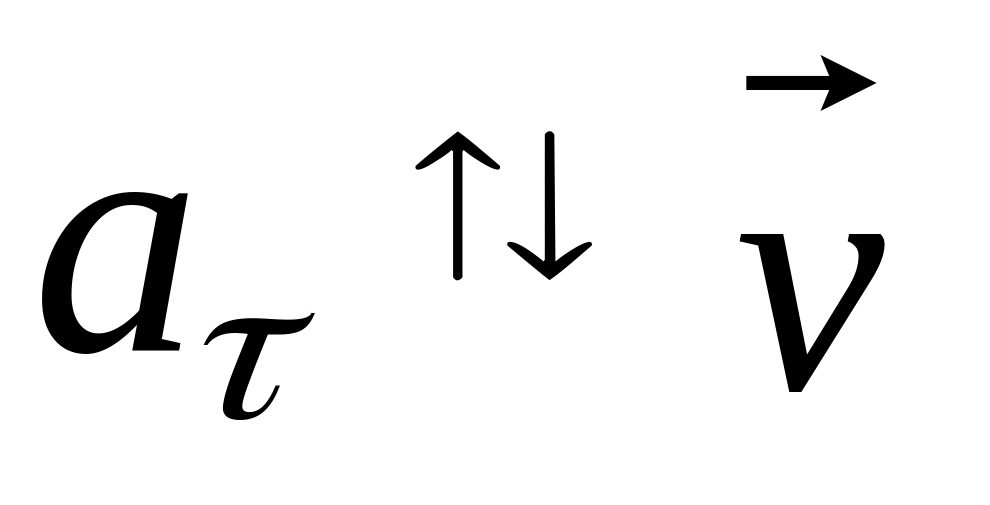
Запишите выражение для векторов скорости и нормального ускорения
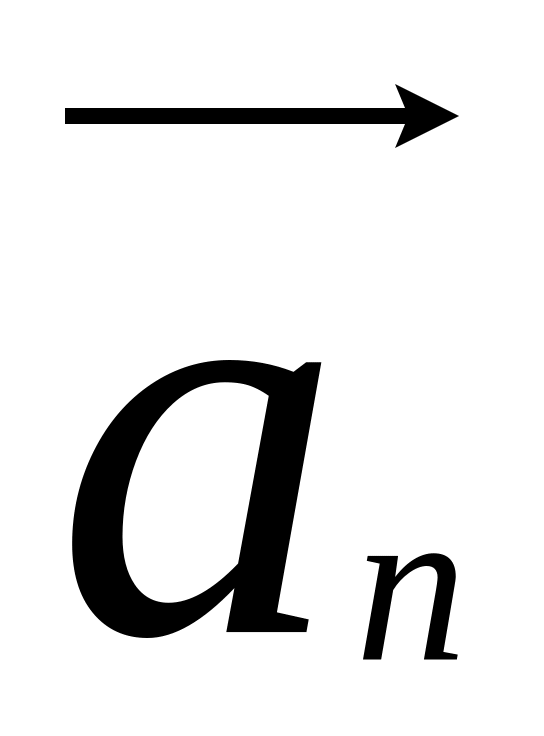 в указанный преподавателем момент
времени и проверьте выполнение условий
в указанный преподавателем момент
времени и проверьте выполнение условий
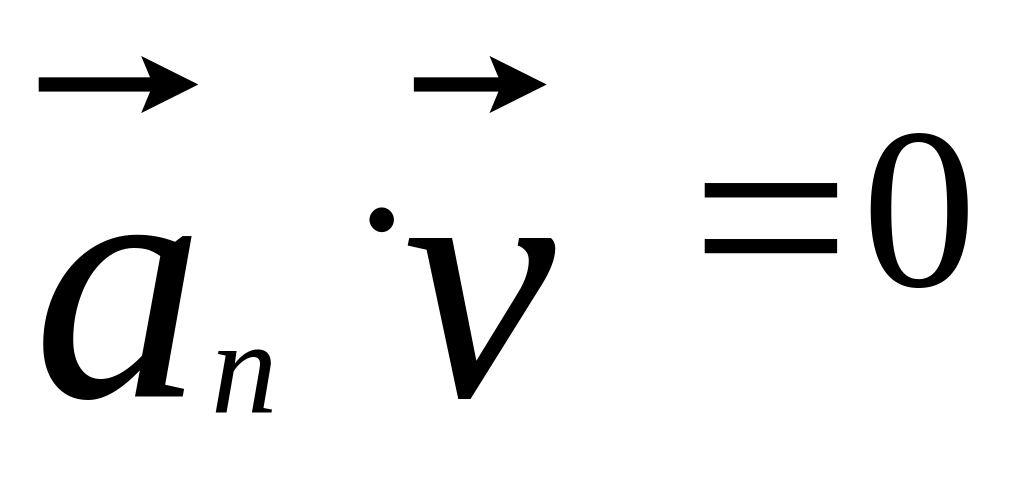
Нанесите экспериментальные точки теоретическую кривую зависимости от времени от времени той координаты, для которой она нелинейна, откладывая вдоль оси абсцисс значения
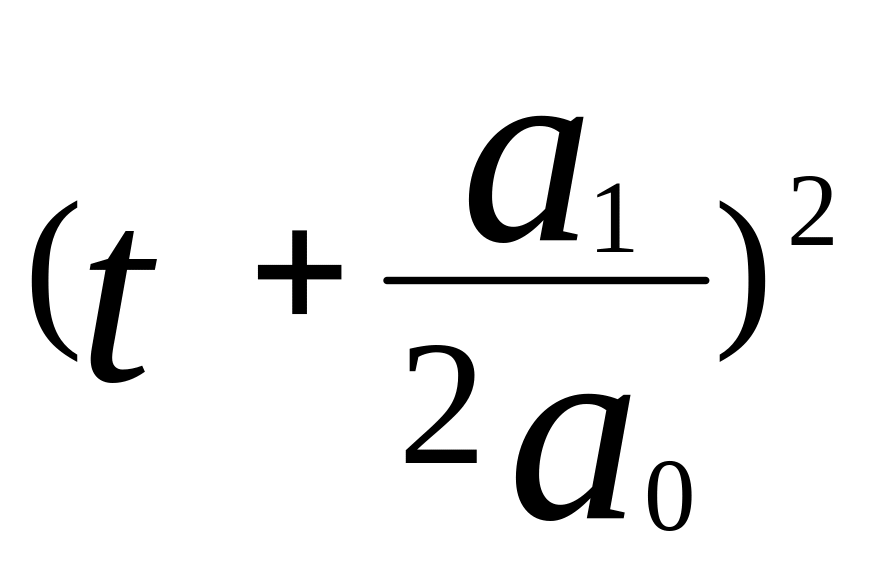 ,
а вдоль оси координат – значения этой
координаты. Сделайте выводы.
,
а вдоль оси координат – значения этой
координаты. Сделайте выводы.
Л И Т Е Р А Т У Р А
1.Сквайрс Дж. Практическая физика. – М.: Мир, 1971. – 246 с.
2.Зендель А.Н. Ошибки измерений физических величин. – Л.:Наука, 1974. – 108с.
3.Физический практикум. / Под ред. Г.С.Кембровского. – Мн.: Из-во «Университетское», 1986. – 352с.
N/P% |
99 |
95 |
90 |
80 |
70 |
50 |
20 |
5 |
4 |
0,8 |
0.7 |
1,1 |
1,6 |
2,2 |
3,4 |
6,0 |
9,5 |
5 |
0,6 |
1,1 |
1,6 |
2,3 |
3,0 |
4,4 |
7,3 |
11,1 |
6 |
0,9 |
1,6 |
2,2 |
3,1 |
3,8 |
5,3 |
8,6 |
12,6 |
7 |
1,3 |
2,2 |
2,8 |
3,8 |
4,7 |
6,3 |
9,8 |
14,1 |
8 |
1,6 |
2,7 |
3,5 |
4,6 |
5,5 |
7,3 |
11,0 |
15,5 |
9 |
2,1 |
3,3 |
4,2 |
5,4 |
6,4 |
8,3 |
12,2 |
16,9 |
10 |
2,6 |
3,9 |
4,9 |
6,2 |
7,3 |
9,3 |
13,4 |
18,3 |
11 |
3,1 |
4,6 |
5,6 |
7,0 |
8,3 |
10,3 |
14,6 |
19,7 |
12 |
3,6 |
5,2 |
6,3 |
7,8 |
9,0 |
11.3 |
15,8 |
21,0 |
13 |
4,1 |
5,9 |
7,0 |
8,6 |
9,9 |
12,3 |
17,0 |
22,4 |
