Введение

В этом учебном году нам предстоит сдавать ЕГЭ по математике, в связи с этим встает вопрос: «Как наиболее эффективно подготовиться к ЕГЭ?». Результаты экзамена по математике за предыдущие годы свидетельствуют о том, что задание части С вызывают большие трудности, особенно задание С-6. Задача С-6 относительно сложная, поскольку требует нестадандартных путей решения. Задача относится к разряду целочисленных. Она требует хорошего понимания свойств делимости, умения производить целенаправленные преобразования выражений для исследования каких-либо специальных свойств, способность логически мыслить, устанавливать взаимосвязи между различными утверждениями. Т.к. свойства чисел по программе изучаются до 9 класса, то возникает необходимость их ещё раз повторить. Кроме того, возможно существуют ещё какие-то методы и способы решения задач на делимость. Поэтому нами выбрана тема: «Решение задач на делимость»

Цель работы:

Овладеть способами и методами, позволяющими решать задания повышенной сложности.

Задачи работы:

1. Повторить, систематизировать и углубить знания о свойствах чисел.

2. Познакомиться с другими методами решения задач на делимость.

3. Применить полученные знания к решению задач типа С6 из вариантов ЕГЭ.

На основе изложенного считаем, что данная работа актуальна и обладает практической ценностью.

1 Делимость целых чисел. Простые и составные числа

1. Свойства чисел

Теория чисел — это ветвь математики, имеющая дело с целыми положительными числами

1, 2, 3, ...,

которые также называют натуральными числами.

Археология и история учат нас, что человек рано начал считать. Сначала он научился складывать числа, потом, много позже, умножать и вычитать их. Деление чисел было необходимым для распределения на равные части кучи яблок или улова рыбы. Эти действия над числами называются вычислениями. В некоторых случаях последовательность вычислений называют «калькуляцией». Это слово происходит от латинского calculus, означающего «маленький камень», поскольку римляне пользовались морской галькой при вычислениях на своих счётных досках.

Как только люди немного научились считать, этот процесс стал приятным времяпровождением для многих людей, склонных к абстрактному теоретизированию. Знания о числах накапливались в течение многих веков, порождая интерес к новым исследованиям, которые в свою очередь приумножали эти накопления. И сейчас, в современной математике, мы имеем величественную конструкцию, известную как теория чисел. Некоторые части этой теории все еще составляют простые игры с числами, а другие относятся к наиболее трудным и сложным разделам математики.

Числа 1, 2, 3 и так далее называются натуральными. Наименьшее натуральное число – это 1, а наибольшего натурального числа не существует. Целые числа – это числа …–3, –2, –1, 0, 1, 2, 3,…; ряд целых чисел можно неограниченно продолжить как вправо, так и влево.

Натуральное число n называется делителем целого числа m, если m=nk для подходящего целого числа k. В этом случае говорят, что m делится на n (нацело) и обозначают этот факт так: m : n (иногда используют обозначение n⎪m, - n делит m). Число m также называют кратным числу n. Каждое число n имеет бесконечное множество кратных: 0, ±n, ±2n, ±3n, ...

Натуральное число, имеющее ровно два различных делителя – само себя и единицу, – называется простым. Целое число, имеющее больше двух различных делителей, называется составным. Наименьшее простое число равно 2. Остальные простые числа являются нечётными. Согласно определению, число 1 – ни простое, ни составное.

Если целые числа m, n делятся на натуральное число с, то с называется их общим делителем. Наибольший общий делитель m и n обозначается НОД(m, n).

Любое целое число, кратное m и n, называется их общим кратным. Наименьшее натуральное число, кратное m и n, называется наименьшим общим кратным m и n. Оно обозначается НОК (m, n).

Числа, не имеющие общих делителей, кроме 1, называются взаимно простыми.

Для разложения чисел на множители или для исследования делимости полезны обобщения формул сокращенного умножения (n – натуральное число):

1. 

2. +

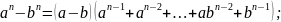
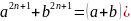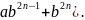
Из этих равенств видно, что при целых a и b делятся соответственно на a-b и a+b.

Cформулируем

Основные свойства делимости.

Делителем натурального числа называется всякое натуральное число, на которое данное число делится без остатка.

Кратным натурального числа называется всякое натуральное число, которое делится на данное без остатка.

Например, делителем числа 72 являются числа 1,2,3,4,6,8,12,18,24,36,72. Кратными числа 15 являются числа 15,30,45,60,75,…

Признаком делимости называют правило, посредством которого можно установить делимость одного числа на другое, не выполняя действия деления.

Признак делимости суммы:

Теорема 1. Если каждое слагаемое делится на какое-либо число, то и их сумма разделится на это число.

Теорема, обратная теореме 1, неверна. Если сумма делится на какое-либо число, то и их сумма разделится на это число.

Теорема 2. Если одно из слагаемых не делится на какое либо число, а все остальные слагаемые делятся, то сумма не разделится не это число.

Теорема, обратная теореме 2,также неверна.

Замечание. Если больше одного слагаемого не делится на некоторое число, то о делимости суммы ничего определенного сказать нельзя ( сумма может либо делиться, либо не делиться на это число).

Признак делимости разности:

Теорема 1. Если уменьшаемое и вычитаемое делятся на некоторое число, то на это число делится и разность.

Теорема 2. Если уменьшаемое (вычитаемое) делится на некоторое число, а вычитаемое (уменьшаемое) не делится, то и разность на это число не разделится.

Теоремы, обратные теоремам 1 и 2, неверны.

Замечание. Если и уменьшаемое и вычитаемое не делится на некоторое число, то о делимости разности ничего определенного сказать нельзя (разность может делится или не делится на это число).

Признаки делимости произведения:

Теорема 1. Если хотя бы один из сомножителей делится на некоторое число, то и произведение разделится на это число.

Обратная теорема не верна.

Теорема 2. Если первое число делится на второе, а второе делится на третье, то первое число делится на третье.

Теорема 3. Если одно число не делится на другое, то оно не может делиться на любое кратное другому числу.

Теорема 4. Если некоторое число делится на произведение нескольких сомножителей, то оно делится и на каждый из них.

Теорема обратная теореме 4, неверна. Однако верна теорема:

Теорема 5. Если данное число делится на каждое из нескольких попарно взаимно простых чисел, то оно делится и на их произведение.

Признаки делимости на некоторые числа.

Числа, которые делятся на 2 (без остатка), называются четными, а которые не делятся на 2 – нечетными. Цифры 0, 2, 4 , 6, 8 – четные; цифры 1, 3, 5, 7, 9 – нечетные.

Всякое четное число k может быть представлено в виде k=2n, а нечетное – в виде k=2n-1, где n – натуральное число (в общем случае n – целое число).

На 2 делятся все те и только те числа, которые оканчиваются четной цифрой.

На 5 делятся все те и только те числа, которые оканчиваются цифрой 0 или 5.

На 4 (на 25) делятся все те и только те числа, которые оканчиваются двумя нулями или две последние цифры которых составляют число, делящиеся на 4 (на 25).

На 3 делятся все те и только те числа, сумма цифр которых делится на 3. На 9 делятся всеете и только те числа, сумма цифр которых делится на 9.

На 6 делятся все те и только те числа, которые делятся и на 2 и на 3.

На 8 (на 125) делятся все те и только те числа, которые оканчиваются тремя нулями или три последние цифры которых изображают число. делящееся на 8 (на 125).

На 10 делятся все те и только те числа, которые оканчиваются нулем.

На 7 (на 11 или на 13) делятся все те и только те числа, у которых разность между числом, изображенным тремя последними цифрами, и числом, изображенным остальными цифрами (или наоборот), делится на 7 (на 11 или на 13). Существует более простой признак делимости на 11: на 11 все те и только те числа, у которых сумма цифр, стоящих на четных местах, равна сумме остальных цифр или отличается от нее на число, делящееся на 11.

Разложение составных чисел на произведение простых. Основная теорема арифметики: всякое составное число можно представить в виде произведения простых чисел и при том единственным способом (порядок множителей не учитывается).

Чтобы разложить данное число на простые множители, надо сначала проверить по таблице простых чисел, не является ли оно простым. Если число оказалось составным , то, пользуясь признаками делимости, проверяют последовательно, на какое из простых чисел 2, 3, 5, 7, … оно делится; затем аналогично поступают с частным, полученным после деления. Этот процесс продолжают до тех пор, пока в частном не получится простое число.

Одни и те же простые множители в разложении составного числа могут встречаться несколько раз. Например, 360=2*2*2*3*3*5. Для обозначения произведения одинаковых сомножителей вводится понятие степени.

Произведение одинаковых сомножителей называются степенью. Сомножитель этого произведения называются основанием степени, а количество сомножителей называется показателем степени. Обозначение: 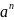, где а – основание степени, n – показатель степени.

Следовательно, по определению, =a*a*a***a, n раз.

Пользуясь определением степени, разложение числа 360 на простые множители можно записать 360=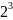 * *5.

Наибольшим общим делителем (НОД) нескольких чисел называется наибольшее натуральное число, на которое делятся все эти числа.

Общие делители нескольких чисел обозначим d, а наибольший общий делитель D.

Для двух чисел a и b записывают D=(a,b); аналогично для нескольких чисел. Например, число 24 имеет делителями числа 1, 2, 3, 4, 6, 8, 12, 24; число 36 имеет делителями числа 1, 2, 3, 4, 6, 9, 12, 18, 36. Тогда d=d (24, 36) – 1, 2, 3, 4, 6, 12; D=(24, 36)=12/

Два числа, имеющие НОД единицу, называются взаимно простыми.

Для получения НОД нескольких данных чисел достаточно разложить каждое число на простые множители, выписать общие простые множители для всех дынных чисел и перемножить их. Найдем, например, НОД чисел 18, 48, и 72.

Разложим каждое из чисел на простые множители: 18=2*3*3; 48=2*2*2*2*3; 72=2*2*2*3*3. Выписываем общие для всех чисел простые множители 2 и 3; тогда

D= (18, 48, 72) =2*3=6.

Для нахождения наибольшего общего делителя двух данных чисел существует так называемый алгоритм Евклида, основанный на последовательном делении. Алгоритм Евклида строится на основание следующих свойств НОД:

а) если первое число делится на второе число, то второе число есть НОД этих чисел;

б) если первое число не делится на второе, то НОД этих чисел равен НОД второго числа и остатка, полученного при делении первого числа на второе.

Чтобы найти НОД двух данных чисел при помощи алгоритма Евклида, надо большее число разделить на меньшее; если деление выполнилось без остатка, то НОД есть меньшее число. Если при делении получится остаток, то меньшее число нужно разделить на этот остаток; затем первый остаток разделить на второй и т.д. до тех пор, пока деление не выполнится без остатка. Первый делитель, при котором деление выполнится без остатка. Первый делитель, при котором деление выполнится без остатка, и будет НОД двух данных чисел. Найдем, например, НОД чисел 112 и 80. При делении 112 на 80 получаем в остатке 32 (112=80*1+32). При делении 80 на 32 получаем в остатке 16 (80=32*2+16). Деление 32 на 16 выполнилось без остатка (32=16*2). Следовательно, НОД чисел 112 и 80 равен 16, т.е. D=(112;80)=16.

Некоторые свойства НОД:

а) частные от деления данных чисел на их НОД есть взаимно простые числа;

б) если умножить каждое из данных чисел на одно и то же число, то и из НОД умножится на это число;

в) всякий общий делитель данных чисел есть делитель их НОД;

г) всякий делитель НОД данных чисел есть общий делитель этих чисел.

Наименьшим общим кратным (НОК) данных чисел называется наименьшее натуральное число, которое делится на все данные числа. Например, кратным числа 8 есть числа 8,16,24,32,40,48,…;кратным числа 12 есть числа 12,24,36,48,60,… Общими кратными чисел 8 и 12 есть числа 24, 48,… Наименьшим общим кратным чисел 8 и 12 есть число 24. Это записывают так: m=(8;12)=24.

Чтобы найти Нок нескольких чисел, достаточно разложить эти числа на простые множители, затем выписать все множители из наибольшего числа и к ним дописать недостающие множители из остальных чисел (учитывая количество одинаковых множителей). Например, чтобы найти НОК чисел 12,16,18, достаточно разложить каждое из чисел на простые множители (12=2*2*3; 16=2*2*2*2; 18=2*3*3), затем выписать все простые множители числа 18, и дописать к ним недостающие множители из разложений чисел 12и 16. Следовательно, m=(12;16;18)=2*3*3*2*2*2=144.

Между НОК и НОД двух чисел существует взаимная связь, которая выражается теоремой: произведение двух данных чисел равно произведению их НОК и НОД.

Пользуясь этой теоремой, НОК двух чисел a и b, можно найти как частное от деления произведения ab этих чисел на их НОД, т.е.

m=ab/D,

а НОД – как частное от деления произведения ab этих чисел на их НОК, т.е.

D=ab/m.

Некоторые свойства НОК:

а) частное от деления НОК данных чисел на эти числа есть взаимно простые числа;

б) если каждое из данных чисел умножить на одно и то же число, то и их НОК умножится на это число;

в) если некоторое из данных чисел делится на все остальные, то оно есть НОК данных чисел;

г) если данные числа взаимно простые, то НОК равно их произведению.

Если в разложение на множители числа n встречаются равные простые числа, их удобнее собирать в степени. В результате получается каноническое разложение:

N=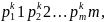

Где P1,…,Pm различные простые числа. Такое разложение абсолютно однозначно.

Например, 3780=2*2*3*3*3*5*7=

Задача разложения чисел, особенно больших, весьма трудоемкая. Уже поиск первого простого делителя может оказаться сложным. На практике можно использовать следующее наблюдение:

Если число n составное: n=ab, то квадрат одного из сомножителей не превосходит n.

В самом деле, допустив противное, что 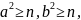мы получили бы, что противоречие.

Попробуйте проверить, что 1997 и 1999 – простые числа (так называемые «близнецы»);

Достаточно проверить простые делители до 43. Следующий простой номер года встретится не так скоро.

Рассмотрим способ разложения на множители натурального числа, не требующий перебора всех возможных его простых делителей. Этот оригинальный метод был предложен знаменитым французским математиком Пьером Ферма (1601-1665). Предварительно выведем простую, но полезную формулу для суммирования последовательных нечетных чисел. Заметим, что 1=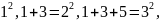

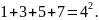Эту закономерность наглядно иллюстрируют картинки – один квадратик плюс три квадратика получим четыре (или 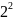) и т.д.

Равенство S=1+3+5+…+(2n-1)=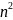 для любого числа n можно получить также из формулы, предшествующей примеру 2: 1+3+5+…+(2n-1)+(2+4+…+(2n-2))=2n(2n-1), откуда

S=n(2n-1)-2n(n-1)/2=

Теперь изложим метод Ферма. Пусть n ≥ 3 – нечетное число. Будем прибавлять к нему последовательно нечетные числа 1, 3, 5, 7 и т.д., пока не получим квадрат некоторого числа L.

Итак, n+1+3+5+7+…+(2k-1)=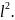 Так как 1+3+5+…+(2k-1)= 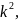то n=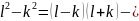 искомое разложение числа n.

Зная каноническое разложение чисел, можно многое сказать об этих числах.

Можно найти все делители числа n = то они имеют вид d где каждый показатель степени 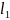, может принимать значения от 0 до , i=1,…,m. Делитель будет собственным (т.е. меньшим числа n), если ≤ хотя бы для одного i.