Высшая Математика КР3 5 Вариант АСОИ

УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Факультет заочного и дистанционного обучения

Специальность: Автоматизированные системы обработки информации

КОНТРОЛЬНАЯ РАБОТА

ПО ВЫСШЕЙ МАТЕМАТИКЕ № 3

Вариант № 5

Маленького Евгения Николаевича

Группа: 000622

Зачетная книжка: 000622-25

Электронный адрес: 12_09_79@mail.ru

Задача 85

Выделив в заданной функции полный квадрат, получить уравнение параболы и построить ее график.

.

Выделим полный квадрат в заданной функции :

;

;

;

Д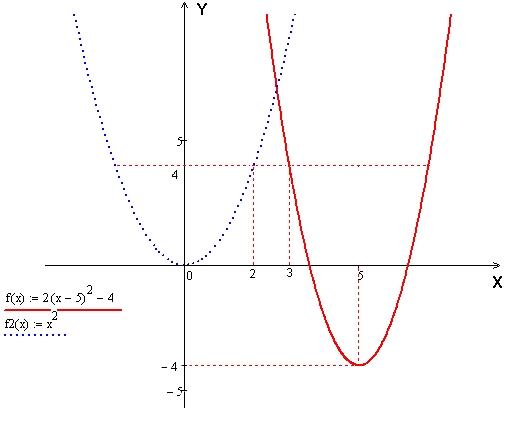алее применим метод преобразования координат. График функции – получают путем переноса графика вдоль оси на – верх или вниз в зависимости от знака . График – получается параллельным переносом графика по оси , при c > 0 – в отрицательном, а при c < 0 – в положительном направлении на . График функции получается растяжением графика вдоль оси в раз при > 1 или сжатием в раз при 0 < < 1. В нашем случае график заданной функции получится путем переноса вершины параболы в точку , а затем растянув параболу в 2 раза вдоль оси .

Задача 95

Задана функция на отрезке . Требуется: 1) построить график функции в полярной системе координат по точкам, давая аргументу значения через промежуток ; 2) найти каноническое уравнение линии в прямоугольной декартовой системе координат, начало которой совпадает с полюсом, а положительная полуось абсцисс – с полярной осью, и по уравнению определить тип линии.

.

1) Построить график функции в полярной системе координат по точкам, давая аргументу значения через промежуток .

Составим таблицу значений аргумента и функции:

	0
r	5	4,07	≈2,661	≈1,753	1,25	≈0,971	≈0,817	≈0,738	≈0,714

r	≈0,738	≈0,817	≈0,971	1,25	≈1,753	≈2,661	4,07	5

Для вычерчивания линии проведем радиус-векторы, соответствующие углам , взятым с интервалом . На каждом из этих радиус-векторов откладываем отрезки, численно равные значению r при соответствующем значении из таблицы. Соединяя точки, являющиеся концами этих отрезков, получим график данной линии.

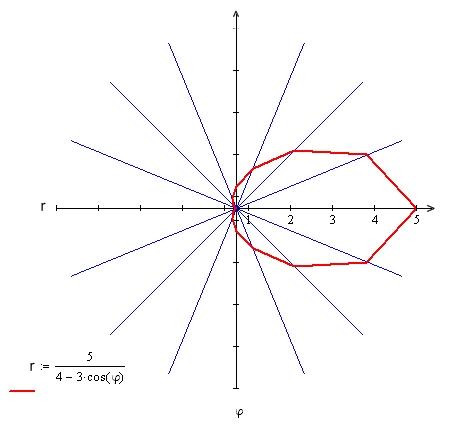
2) Найти каноническое уравнение линии в прямоугольной декартовой системе координат, начало которой совпадает с полюсом, а положительная полуось абсцисс – с полярной осью, и по уравнению определить тип линии.

Подставляя и в уравнение, имеем:

;

;

;

;

;

;

;

;

;

;

.

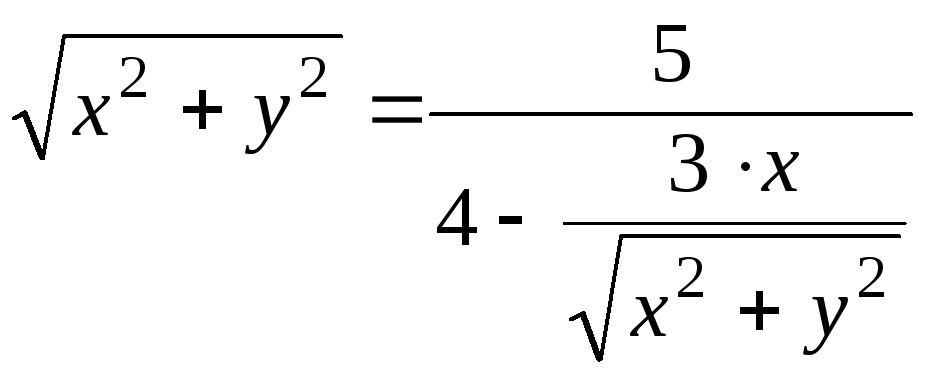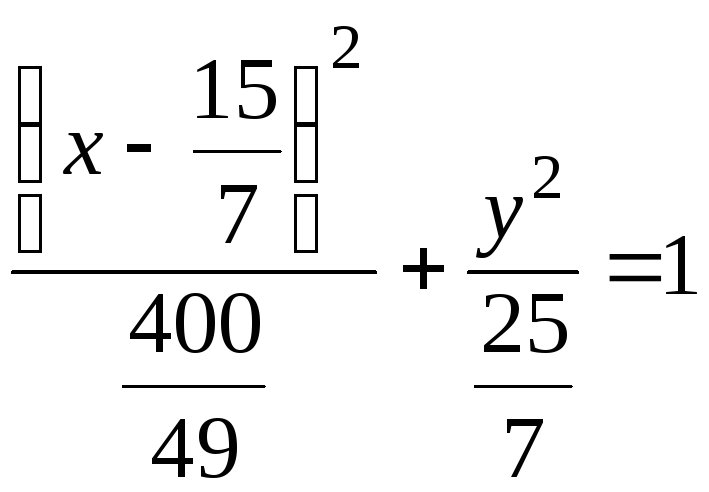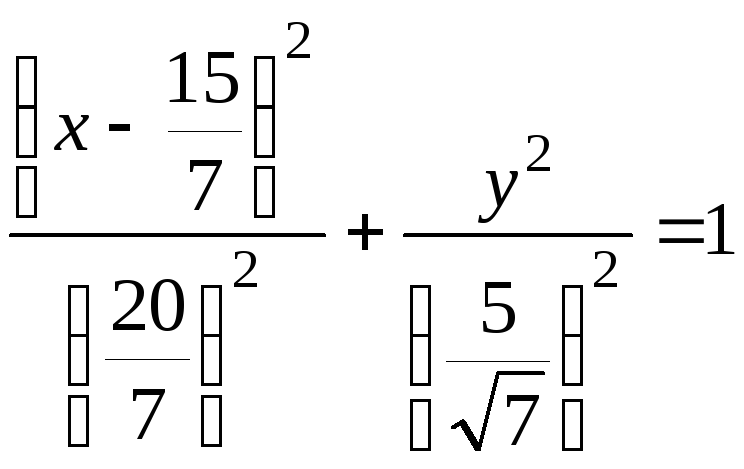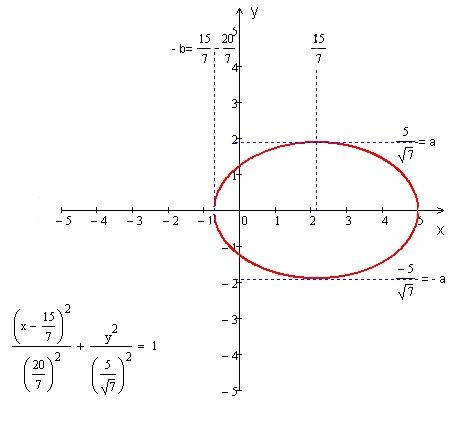
Полученное уравнение – это каноническое уравнение эллипса с центром в точке и полуосями , .

Задача 105

Найти указанные пределы, не пользуясь правилом Лопиталя.

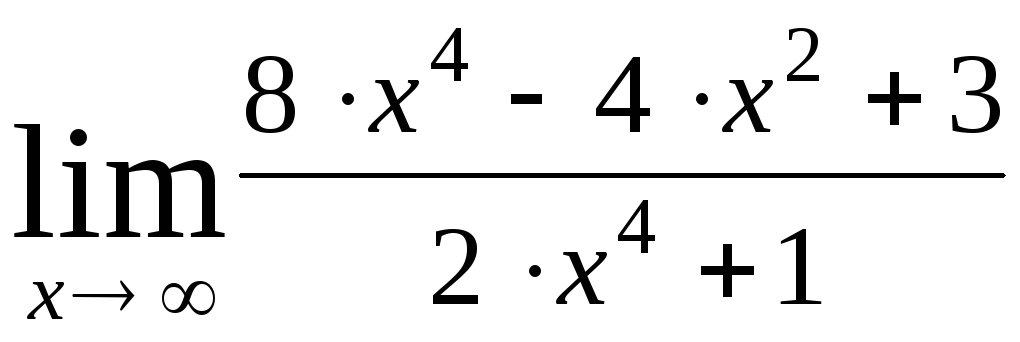1. ; 2) ;

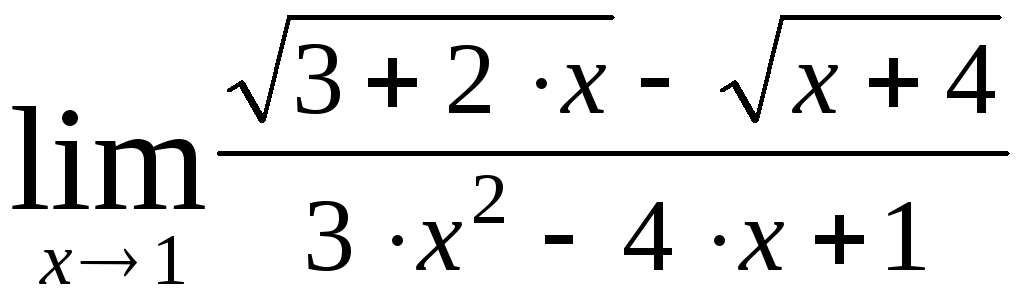3) ;

1) Найти данный предел, не пользуясь правилом Лопиталя.

;

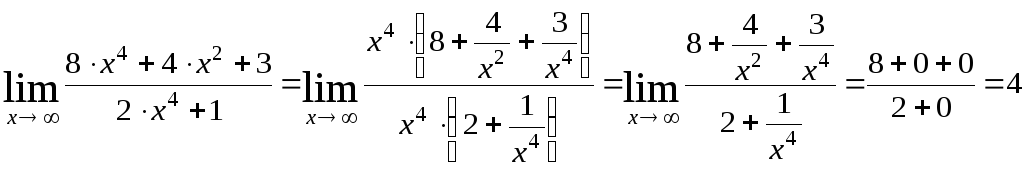2) Найти данный предел, не пользуясь правилом Лопиталя.

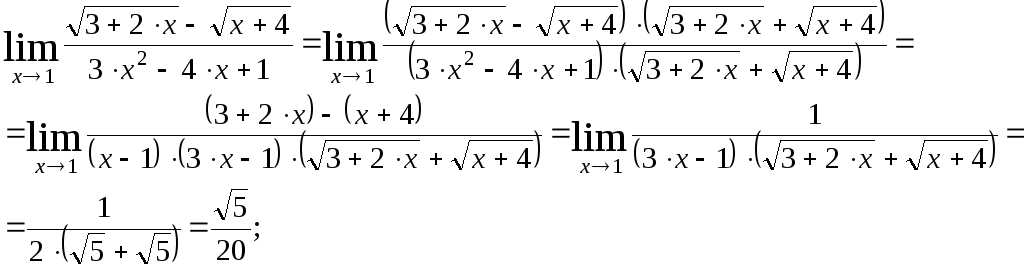
3) Найти данный предел, не пользуясь правилом Лопиталя.

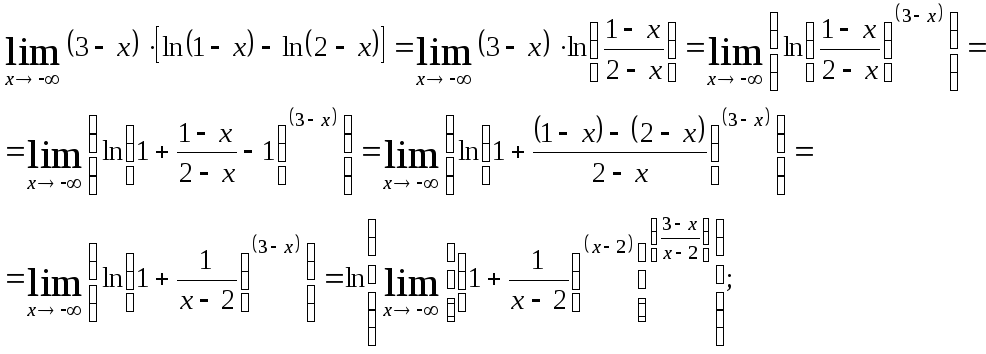
Выражение в квадратных скобках есть не что иное, как второй замечательный предел, т.е. число e, а предел показателя степени найдем отдельно:

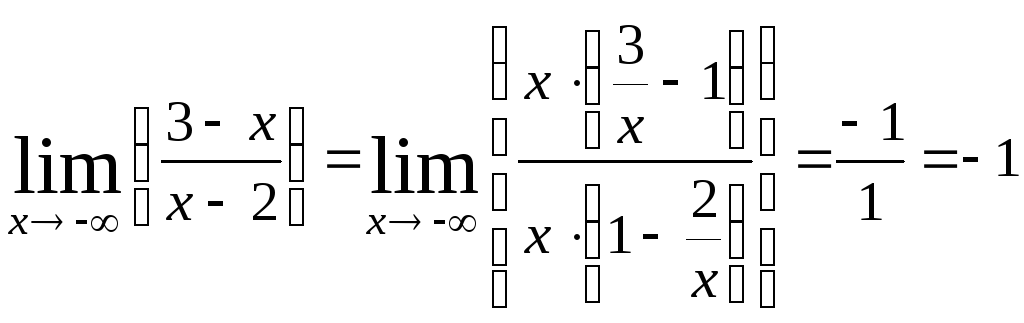; Следовательно:

;

Задача 115

Найти указанные пределы, используя эквивалентные бесконечно малые функции.

1. ; 2) ;

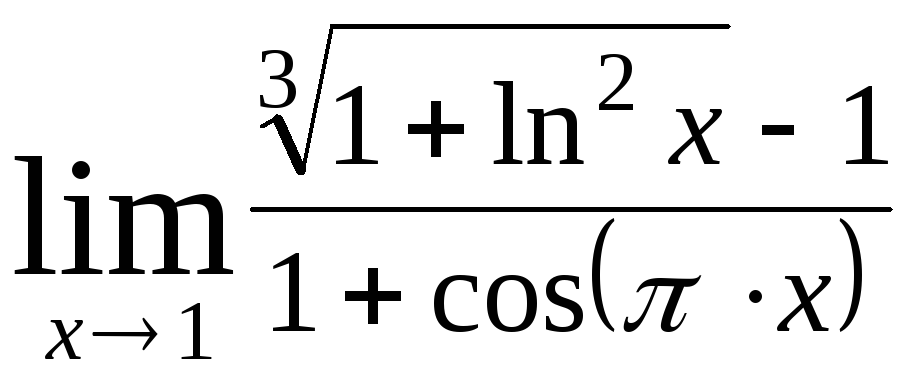1) Найти данный предел, используя эквивалентную бесконечно малую функцию.

.

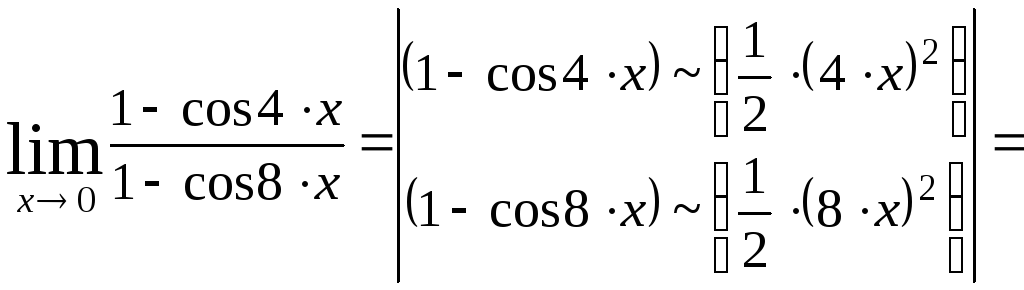
2) Найти данный предел, используя эквивалентную бесконечно малую функцию.

Т.к. аргумент косинуса не является бесконечно малой функцией, при , то введем замену переменной , при , , :

.

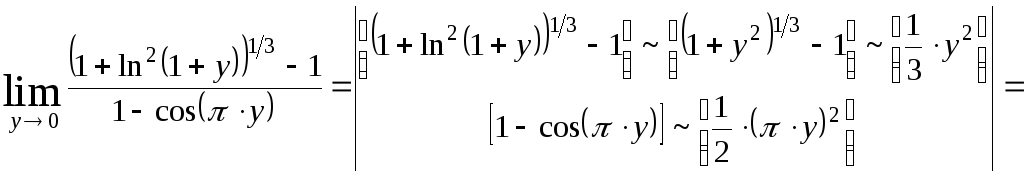
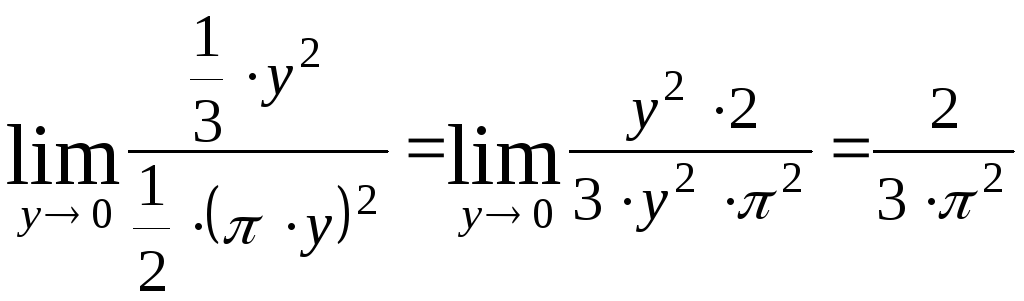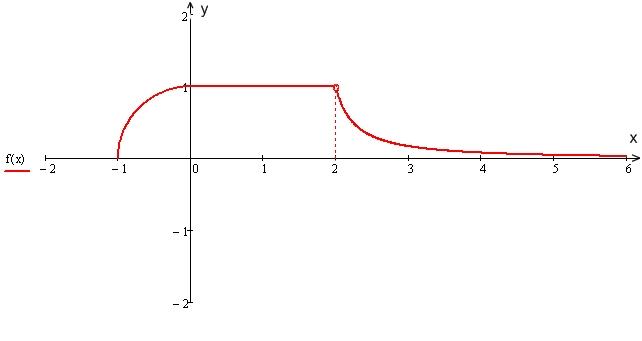
Задача 125

Задана функция различными аналитическими выражениями для различных интервалов изменения аргумента. Найти точки разрыва функции, если они существуют, и установить их тип. Сделать чертеж.

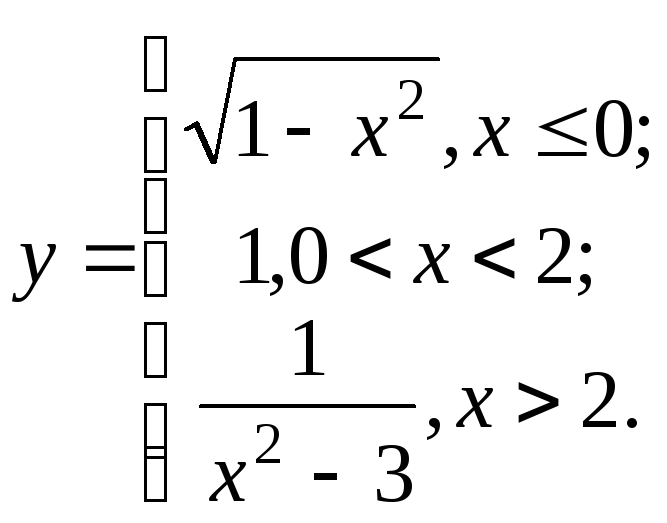
Функция неэлементарная, т.к. задана аналитически. На интервалах она задана аналитически элементарными функциями, определена на каждом и является непрерывной. Исключением являются точки где функция меняет свое аналитическое выражение, поэтому исследуем эти точки (x = 0 и x = 2 ) на непрерывность, для этого вычислим односторонние пределы:

;

;

;

В точке x = 0 – непрерывна, т.к. существуют правый и левый пределы, они равны и равны значению функции в этой точке;

;

;

– не определена;

В точке x = 2 находится точка устранимого разрыва, т.к. правый и левый пределы существуют и равны, а функция в данной точке не определена. В этой точке находится разрыв I-го рода.