
Контрольная работа №5 вариант 5
.pdf
Контрольная работа № 5
№ 225
Найти общее решение дифференциального уравнения первого порядка:
x ycos xy dx xcos xy dy 0
Преобразуем
|
y |
|
|
|
|
|
|
|
|
||||
x ycos |
|
|
|
|
dy |
|
y |
|
1 |
|
|
||
|
|
|
|
|
|
||||||||
|
x |
|
y |
|
|
|
|||||||
|
|
dx |
|
|
|
|
|||||||
y |
|
x |
y |
||||||||||
xcos |
|
|
|
|
|
|
|
|
|
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x |
|
|
|
|
|
x |
|||||||
Делаем замену y ux, получаем y u x dudx .
Подставляем y и u xy в предыдущее уравнение получаем:
u x dudx u cos(1u) или x dudx cos(1u) cos(u)du dxx
Интегрируем правую и левую части:
cos(u)du dxx sin(u) ln(x) C
Подставляя вместо u его значение, окончательно получаем
sin y ln(x) C
x
№ 235
Найти частное решение дифференциального уравнения, удовлетворяющее указанным начальным условиям:
y 4y 4y 2(sin2x x); |
y(0) 0; y (0) 1. |
Составим характеристическое уравнение однородного уравнения:
k2 4k 4 0 k1,2 2
Значит, общее решение однородного уравнения будет иметь вид:
u (C1 C2 x)e2x
Частное решение ищем в виде:
y1 Asin2x Bcos2x Cx D
y1 2Acos2x 2Bsin2x C y1 4Asin2x 4Bcos2x
Значит
4Asin2x 4Bcos2x 4(2Acos2x 2Bsin2x C) 4(Asin2x Bcos2x Cx D)
2(sin2x x)
sin2x : 4A 8B 4A 2 cos2x : 4B 8A 4B 0 x1 : 4C 2
x0 : 4C 4D 0
A 0;B 14;C D 12
Тогда получаем, что y1 14 cos2x 12 x 12
Следовательно, общее решение имеет вид:
y (C1 C2x)e2x 14 cos2x 12 x 12
Так как по условию имеем y(0) 0; y (0) 1 , то
0 C1 14 12 C1 34
y C2e2x 2(C1 C2x) 12sin2x 12
1 C2 2C1 12 C2 0
Окончательно получаем
y 14 cos2x 3e2x 2x 2

№ 245
Найти общее решение системы уравнений.
dxdt 3x y
dy x 3y
dt
Выражаем dydt :
dydt 3 dxt 8x
Продифференцируем по t первое уравнение:
d22x 3dx dy 0 dt t dt
ddt22x 6dxt 8x 0
Составим характеристическое уравнение:
k2 6k 8 0 k1 2;k2 4
Следовательно, общее решение для x:
x C1e2t C2e4t
Находим общее решение для y:
y dxdt 3x 2C1e2t 4C2e4t 3C1e2t C2e4t C1e2t C2e4t
Получаем окончательное решение системы уравнений:
x C1e2t C2e4t
y C1e2t C2e4t
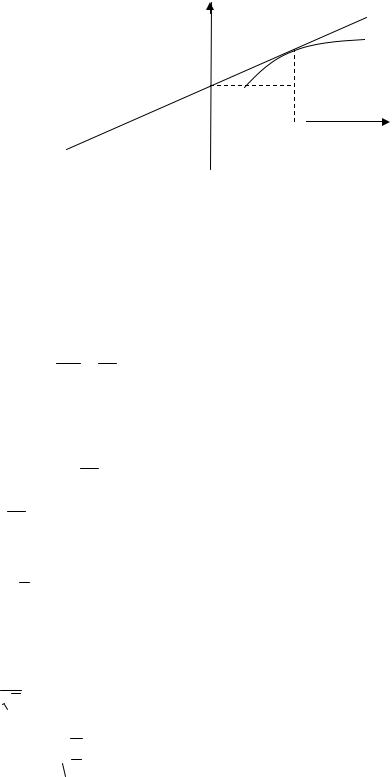
№ 255
Найти уравнение кривой, проходящей через точку (3;1) и обладающей тем свойством, что отрезок касательной между точкой касания и осью Ох делится пополам в точке пересечения с осью Оу.
у
M(x,y)
A B
Q O |
C |
x |
|
|
|
|
|
По условию QA AM
Получаем, что треугольник QAO и AMBравны (по двум углам и стороне).
Значит BC MB.
tg MB 12 y y AB x 2x
Из геометрического смысла производной имеем:
y tg y 2yx dydx 2yx dyy 2dxx ln y 12lnx lnC y C
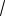 x
x
Так как линия проходит через точку (3;1) , находим:
C 1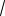 3
3
Ответ: y 
 3x .
3x .
