Глава 3. Переходные процессы в электрических

цепях

3.1. Понятие переходного процесса, ступенчатый входной сигнал

Переходным процессом называется процесс, характеризующийся переходом электрической цепи из одного электрического устойчивого состояния в другое электрическое устойчивое состояние в течение некоторого времени.

Переходные процессы возникают в результате каких-либо изменений в электрической цепи. Простейшим примером может служить включение какого-либо электротехнического устройства, которое состоит в том, что на него подаётся напряжение питания. С момента подачи напряжения до момента, когда это устройство начинает функционировать проходит некоторое время, в течение которого осуществляется переходный процесс из одного устойчивого состояния (выключен) в другое (включён). Действия, в результате которых возникает переходный процесс, называются коммутационными действиями или коммутацией.

Переходные процессы возникают только в тех электрических устройствах, которые содержат энергоёмкие элементы, то есть элементы, которые способны накапливать и отдавать энергию. Такими элементами, как известно, являются индуктивность и конденсатор. При наличии в схеме только резисторов электрические процессы протекают мгновенно, т. е. переходные процессы тогда отсутствуют.

Для большинства устройств присутствие переходного процесса нежелательно. Так как переходный процесс проходит в течение некоторого времени, то происходит задержка реакции схемы на входной сигнал. При переходном процессе возникают режимы, которые могут оказаться аварийными для устройства.

Анализ переходного процесса осуществляется подачей на вход схемы напряжения ступенчатой формы (рис. 3.1) и исследованием поведения выходного сигнала. За начало переходного процесса берется момент времени t = 0. Ступенчатый входной сигнал имеет определенную величину U_m. До момента t = 0 входной сигнал отсутствует (U_вх= 0), а в момент времени t = 0 он принимает значение U_m (U_вх= U_m) и остается постоянным.

Д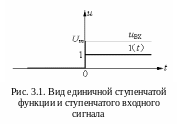 ля аналитического описания ступенчатого входного сигнала используется единичная ступенчатая функция 1(t), удовлетворяющая следующим требованиям:

.

Тогда входной ступенчатый сигнал принимает вид:

. (3.1.)

П ри подаче ступенчатого сигнала (3.1) на вход исследуемого устройства форма его выходного напряжения зависит от схемного решения этого устройства. На рис. 3.2 показаны возможные формы выходного напряжения при воздействии входного сигнала ступенчатой формы. Как видно, изменения выходного сигнала могут иметь экспоненциальный или колебательный характер, а так же нарастающий или убывающий вид. Очевидно, что вид переходного процесса устройства определяется его схемным решением.

Как отмечалось, за начало переходного процесса берется t = 0. Теоретически считается, что переходный процесс заканчивается через t = . Всякое изменение в электрической цепи, приводящее к появлению переходного процесса, называется коммутацией.

3.2. Начальные условия, законы коммутации

Уже отмечалось, что переходные процессы определяются наличием в цепи энергоемких элементов (L и C). Характер переходного процесса в значительной степени зависит от наличия или отсутствия тока в индуктивности или заряда на конденсаторе в начальный момент времени, т. е. перед самым началом переходного процесса.

Электрическое состояние энергоемких элементов перед началом переходного процесса называется начальным условием этих элементов и всей схемы.

Начальные условия бывают нулевыми и ненулевыми. Нулевым начальным условием называется условие, при котором до момента коммутации через индуктивность не протекает ток, а конденсатор не заряжен. Обозначается это так:

i_L(– 0) = 0, и_с(– 0) = 0.

Здесь минус, стоящий перед нулём, говорит о том, что речь идёт о токе и напряжении до подачи на вход схемы ступенчатого сигнала. Если же ток в индуктивности и напряжение на конденсаторе не равны нулю до подачи на вход схемы ступенчатого сигнала, то начальные условия называются ненулевыми.

На рис. 3.3 показаны схемы с нулевым и ненулевым начальными условиями. В схеме рис. 3.3, а до момента замыкания ключа К цепь отключена от источника энергии, на конденсаторе нет напряжения, а через индуктивность не протекает ток. Эта цепь имеет нулевые начальные услов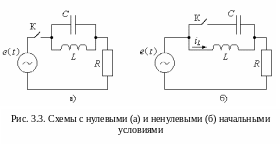 ия:

i_L(– 0) = 0, и_с(– 0) = 0.

В схеме рисунок 3.3, б до момента замыкания ключа К, через индуктивность протекает ток. Начальные условия для этой схемы принято считать не нулевыми и имеют вид:

i_L(– 0) = i_L, и_с(– 0) = 0.

При анализе переходных процессов используются законы коммутации. Законы коммутации основываются на физической невозможности скачкообразного изменения энергии. В связи с этим следует, что энергия индуктивности и конденсатора не может измениться скачком. Отсюда вытекают следующих два закона коммутации.

Закон коммутации для индуктивности:

«В начальный момент после коммутации ток в индуктивности остается таким же, каким он был непосредственно перед коммутацией».

Аналитически закон коммутации для индуктивности отображается так:

i_L(– 0) = i_L(+0). (3.2)

Следствие I.

Исходя из этого закона коммутации, вытекает следующее свойство индуктивности в момент коммутации. При нулевых начальных условиях имеем:

i_L(– 0) = 0 = i_L(+0).

Тогда в момент коммутации, когда к индуктивности прикладывается ступенчатое напряжение U_m, сопротивление индуктивности равно:

.

Значит, при нулевых начальных условиях в момент коммутации индуктивность имеет бесконечное сопротивление, т. е. индуктивность в момент коммутации представляет собой разрыв.

Закон коммутации для конденсатора:

«В начальный момент после коммутации напряжение на конденсаторе остается таким же, каким оно было непосредственно перед коммутацией».

Аналитически закон коммутации для конденсатора представляется так:

. (3.3)

Следствие II.

Рассмотрим, каким омическим свойством обладает конденсатор в момент коммутации. При нулевых начальных условиях имеем:

.

Тогда в момент коммутации сопротивление конденсатора равно:

.

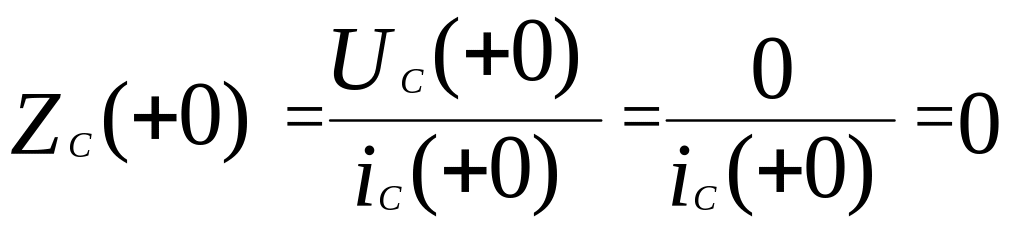Значит в момент коммутации при нулевых начальных условиях сопротивление конденсатора равно нулю, т. е. конденсатор в момент коммутации представляет собой короткое замыкание.

Следствия из законов коммутации позволяют определить электрическое состояние цепи в момент коммутации то есть в начале переходного процесса. На рисунке 3.4,а представлена схема, на вход которой подается ступенчатое напряжение.

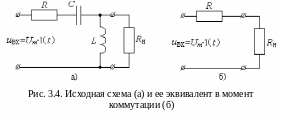
В соответствии со следствиями законов коммутации в момент коммутации конденсатор представляет собой короткое замыкание, а индуктивность – разрыв. На рисунке 3.4,б представлена схема замещения исходной схемы в момент коммутации. Рассчитать ее не сложно и в момент коммутации напряжение на нагрузке равно:

.

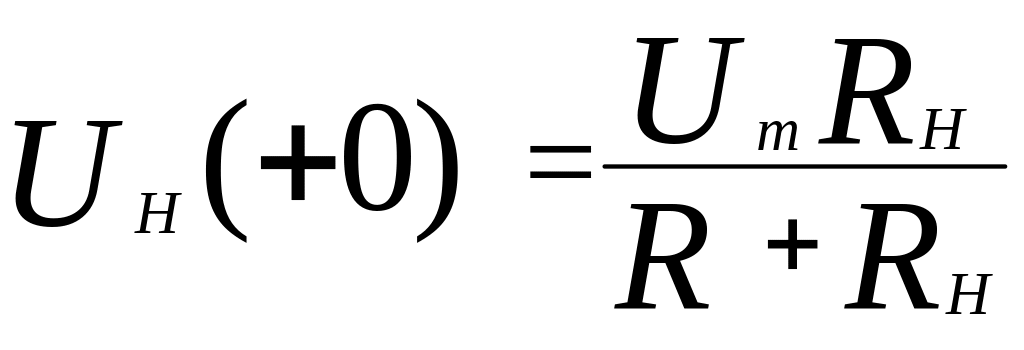3.3. Методы анализа переходных процессов

При анализе переходного процесса цепи рассматривается изменение определенной электрической величины (напряжение, ток) на определенном элементе схемы. Чаще всего таким элементом является нагрузка, подключенная к выходным клеммам схемы. Из электрических величин часто представляет интерес изменение напряжения на нагрузке в переходном процессе.

Все методы расчета переходных процессов можно разделить на два основных метода:

1. Получение аналитического решения с помощью дифференциального уравнения, связывающего выходное напряжение схемы с входным.

2. Применение преобразований Лапласа к анализу переходного процесса.

3.3.1. Анализ переходного процесса путем решения дифференциального уравнения схемы

Этот метод состоит в составлении дифференциального уравнения, связывающего входной сигнал с выходным, и решении этого уравнения известными аналитическими или численными методами. Одним из сложных этапов анализа переходного процесса названным методом является составление дифференциального уравнения для схемы. Рассмотрим два примера.

В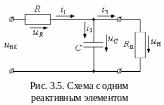 качестве первого примера рассмотри схему с одним реактивным элементом (рис.3.5). Получим для этой схемы дифференциальное уравнение, связывающее входное напряжение и напряжение на нагрузочном резисторе .

Первоначально расставляются условно положительные направления токов и напряжений. Затем с помощью законов Кирхгофа составляются уравнения. Так как в схеме три ветви и три неизвестных тока, то необходимо составить три уравнения. Так как в схеме два узла, то по первому закону Кирхгофа составляется одно уравнение. Тогда по второму закону Кирхгофа составим оставшиеся два уравнения. Контура будем обходить по часовой стрелке:

. (3.4)

Выразим напряжения через токи в ветвях:

, , . (3.5)

С учетом (3.5) перепишем исходную систему уравнений (3.4):

(3.6)

В последнем уравнении удобнее u_Н сохранить без изменения, так как оно является искомой величиной и войдет в дифференциальное уравнение. Далее методом последовательного исключения из трех уравнений (3.6) получим одно. Предварительно найдём из (3.5) токи в ветвях:

, , .

Первое уравнение системы (3.6) с учетом полученных выражений для токов и, что , принимает вид:

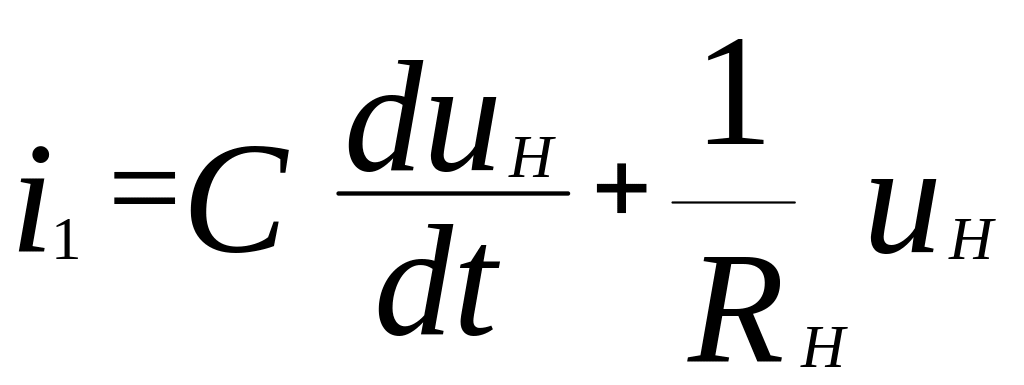. (3.7)

Из третьего уравнения (3.6) находим:

. (3.8)

Подставляем (3.7) и (3.8) во второе уравнение системы (3.6):

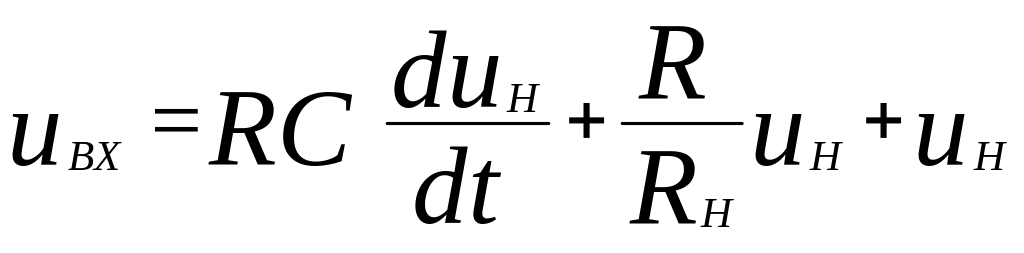. (3.9)

Приведенное дифференциальное уравнение для схемы (рис. 3.5), связывающее напряжение u_Н с входным напряжением u_ВХ принимает вид:

.

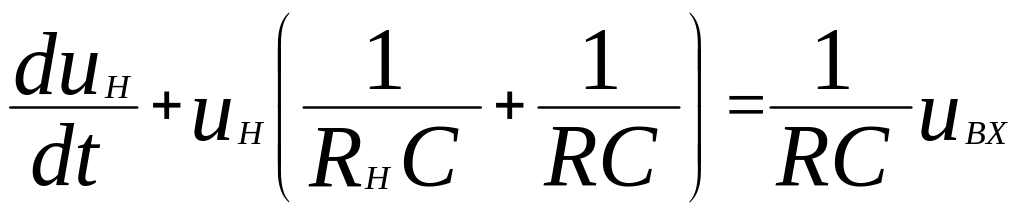Введём следующие обозначения:

, .

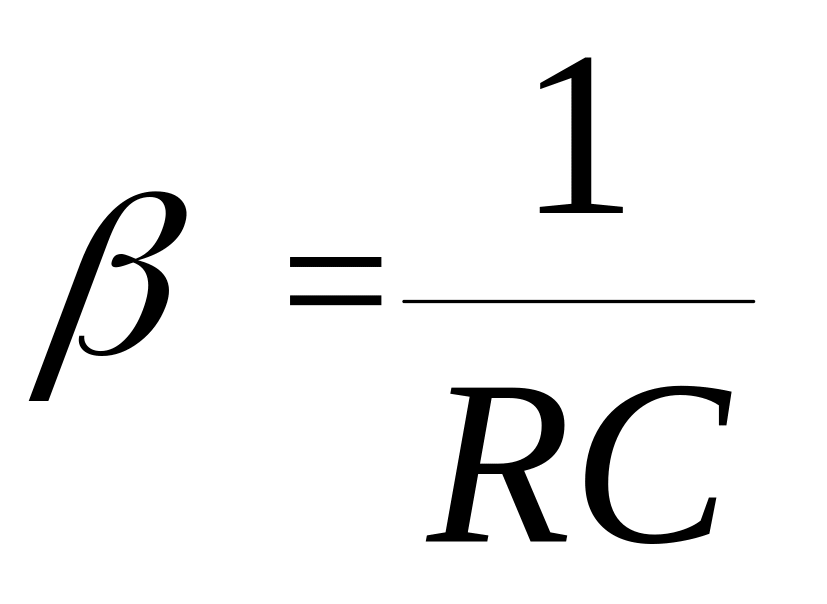С учётом этих обозначений полученное дифференциальное уравнение принимает вид:

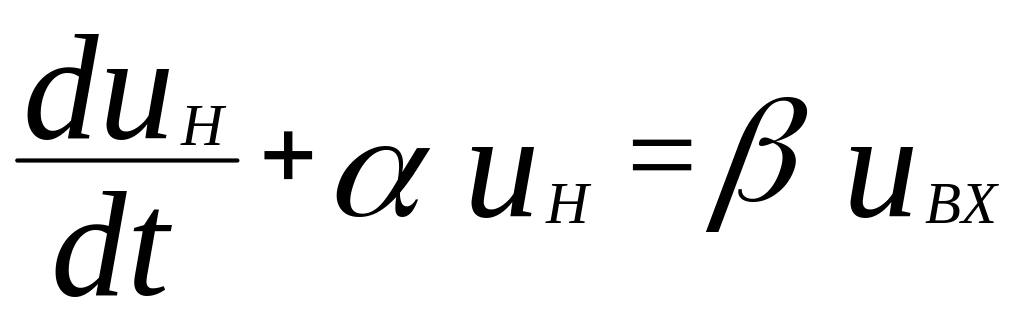(3.10)

Далее решается уравнение (3.10) и находится изменение выходного напряжения во времени под действием входного напряжения ступенчатой формы, которое имеет вид:

.

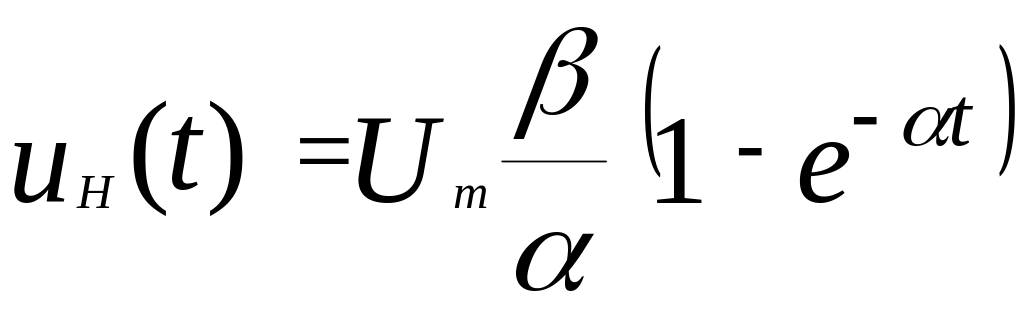Схеме (рис. 3.5) соответствует дифференциальное уравнение первого порядка (3.10). В таких случаях говорят, что данная схема является цепью первого порядка. Следует отметить, что если в схеме присутствует только один тип реактивного (энергоёмкого) элемента – конденсатор или катушка индуктивности, то электрические процессы в переходном режиме в такой схеме всегда описываются дифференциальным уравнением только первого порядка. При этом в схеме может быть один или несколько реактивных элементов, но только одного типа.

Уравнение (3.10) получено путем объединения (обобщения) системы исходных уравнений (3.6). Поэтому такое уравнение еще называют обобщенным дифференциальным уравнением.

Вторым примером будет рассмотрение последовательности получения обобщенного дифференциального уравнения для схемы, содержащей два реактивных элемента различного типа (рис. 3.6).

П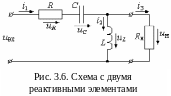 осле расстановки токов и напряжений в схеме записываем исходные уравнения по законам Кирхгофа:

. (3.11)

Выражаем напряжения на элементах схемы через токи:

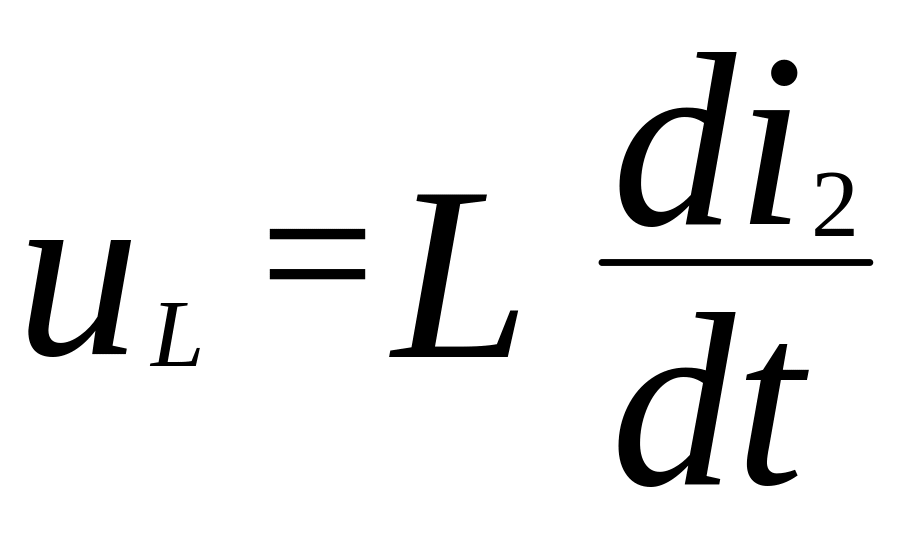, , , . (3.12)

Записываем систему (3.11) с учетом (3.12):

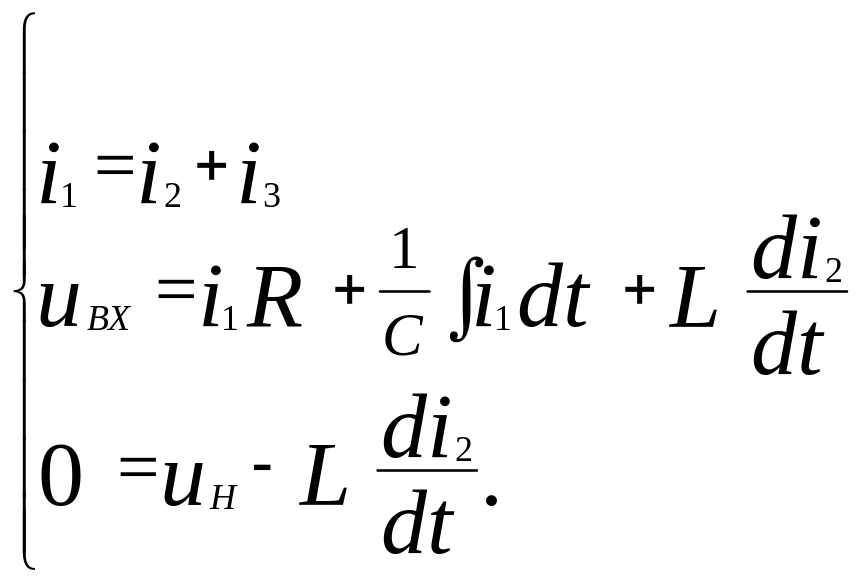. (3.13)

Далее методом последовательного исключения из трех уравнений (3.13) получим одно. Предварительно из (3.12) найдём следующие токи:

, .

Здесь при определении тока было учтено, что .

Подставляем найденные токи в первое уравнение системы (3.13) и оно принимает вид:

. (3.14)

Из третьего уравнения системы (3.13) очевидно равенство:

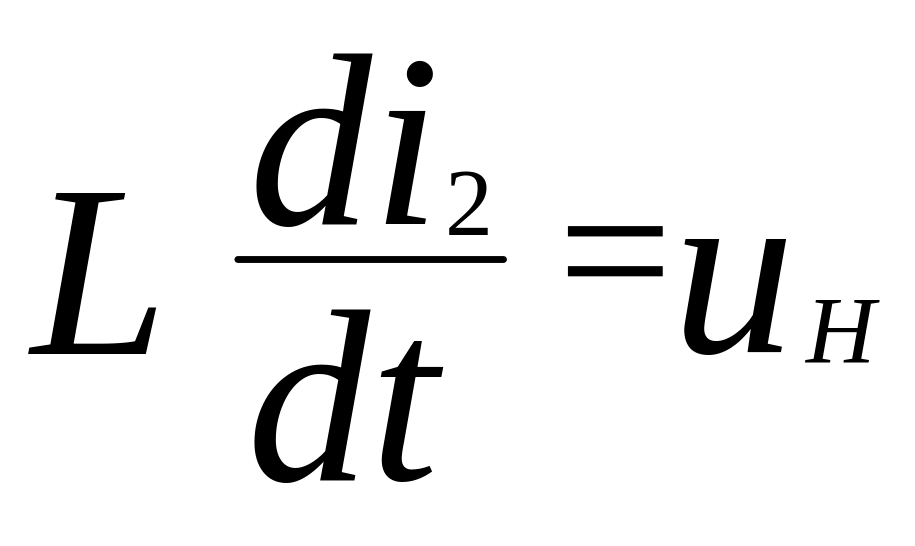. (3.15)

Подставляем (3.14) и (3.15) во второе уравнение системы (3.13):

.

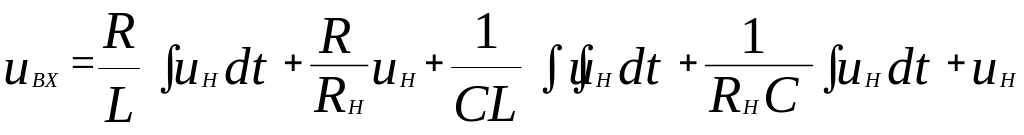Перейдём от полученного интегрального уравнения к дифференциальному, взяв вторую производную от этого уравнения:

.

Приводим подобные члены:

.

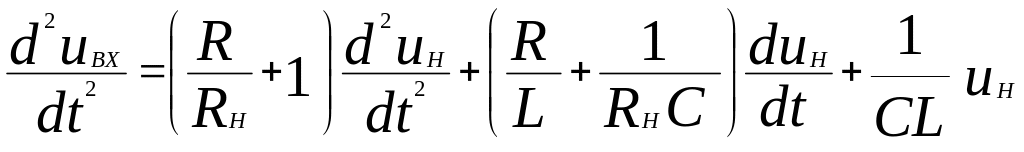Это уравнение можно переписать в более удобном виде:

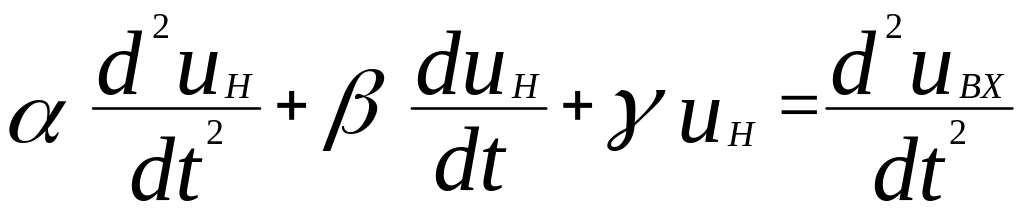, (3.16)

где

, , .

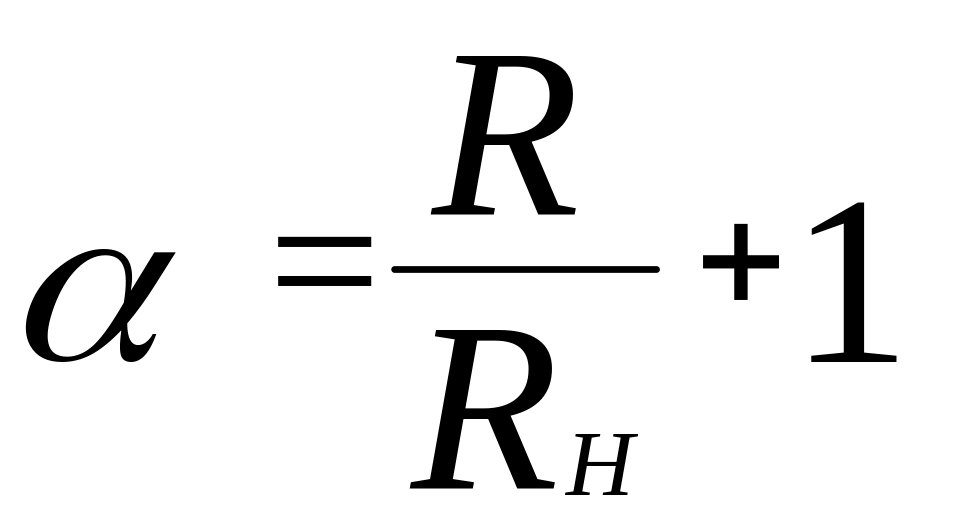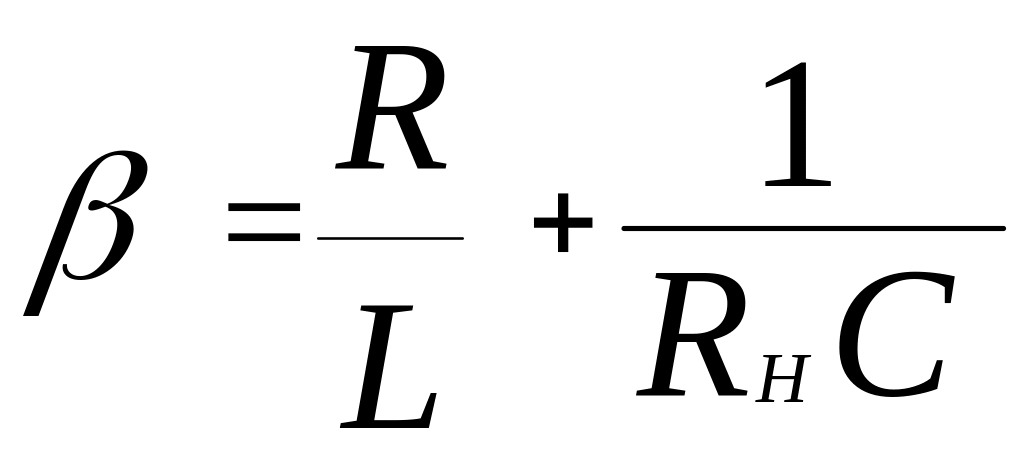Далее уравнение (3.16) решается известными методами.

Схеме (рис. 3.6) соответствует обобщенное дифференциальное уравнение второго порядка (3.16), поэтому такие электрические цепи называются цепями второго порядка. Следует отметить, что в цепях второго порядка всегда присутствуют энергоёмкие элементы двух типов – конденсаторы и катушки индуктивности.

3.3.2. Анализ переходного процесса с помощью преобразований Лапласа

Прежде, чем использовать преобразования Лапласа для анализа электрических цепей необходимо убедиться, что ток и напряжение являются функциями, над которыми можно осуществлять преобразования Лапласа. Как известно, преобразования Лапласа можно осуществлять над функциями, которые возрастают не быстрее показательной функции

, при t>0, (3.17)

где М, С₀ – положительные действительные числа.

Очевидно, что какие бы не были величины тока и напряжения в реальной схеме и сколь быстро они не возрастали, всегда можно выбрать такие значения М и С₀, при которых будет выполняться условие (3.17). Следовательно, осуществляя преобразования Лапласа над током и напряжением, которые называются оригиналами, получаем операторное представление тока и напряжения, которые называются изображениями:

,

,

где р – оператор преобразования Лапласа.

Операцию перехода от оригинала функции к ее изображению можно обозначать так:

,

.

Возможны три последовательности применения преобразований Лапласа при анализе переходных процессов. Рассмотрим их.

Первая последовательность состоит сначала в получении обобщенного дифференциального уравнения схемы, затем преобразовании его по Лапласу, далее нахождении искомой величины в операторной форме (изображение искомой величины) и, наконец, определении оригинала по найденному изображению с помощью обратного преобразования Лапласа. Рассмотрим эту последовательность на примере схемы (рис. 3.5). Для неё обобщенное дифференциальное уравнение имеет вид (3.10). Перепишем его:

.

Выполним преобразования Лапласа над этим уравнением, при этом необходимо помнить, что входное напряжение определяется по (3.1):

.

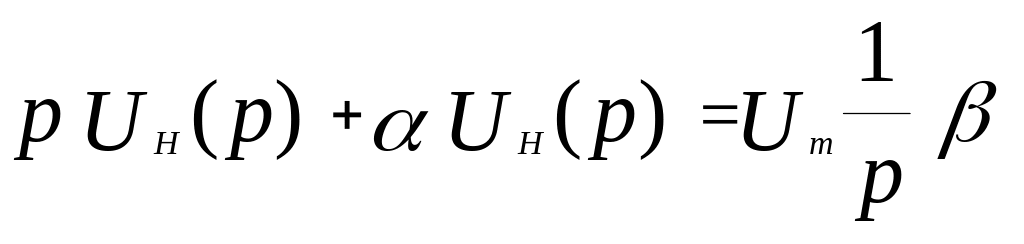Отсюда находим изображение напряжения на нагрузке:

.

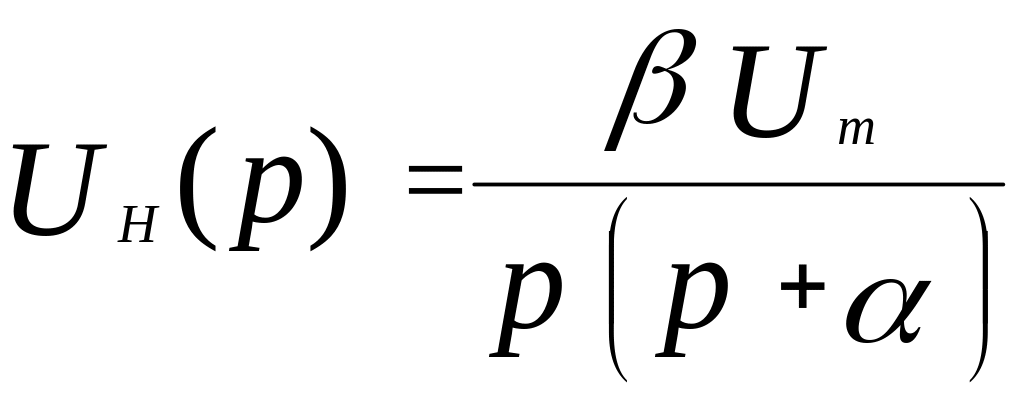Из найденного изображения оригинал искомого напряжения можно определить с помощью обратного преобразования Лапласа. Для типовых изображений составлены таблицы, в которых можно найти оригинал для найденного изображения (Приложение 1). Для полученного изображения оригинал решения имеет вид:

.

Вторая последовательность применения преобразований Лапласа при анализе переходного процесса состоит в преобразовании по Лапласу исходных уравнений схемы. Это приводит к тому, что все уравнения системы становятся алгебраическими, что в дальнейшем облегчает действия над ними. Этот метод удобен в тех случаях, когда исходная система уравнений содержит сложные дифференциально-интегральные уравнения, которые необходимо решать при получении обобщенного дифференциального уравнения. Рассмотрим эту последовательность расчёта на примере схемы рисунок 3.5. Так система уравнений (3.6) после преобразования по Лапласу принимает вид:

.

Выполняя все последующие действия с применением преобразований Лапласа, совершенно очевидно, что будет получено изображение выходного напряжения, полностью совпадающее с выражением, полученным первым методом. Предлагается самостоятельно проверить справедливость этого утверждения.

Третья последовательность применения преобразований Лапласа при анализе переходного процесса состоит в представлении элементов схемы в операторной форме.

В общем случае, как и в цепях переменного тока, сопротивление цепи в операторной форме будем обозначать через Z(р). Сопротивление индуктивности в операторной форме будем обозначать через X_L(р), сопротивление конденсатора в операторной форме будем обозначать через X_C(р), а сопротивление резистора - через R(р). Очевидно, что ток I(р), протекающий через некоторое сопротивление Z(р), создает на нем падение напряжения U(р). Эти величины связаны между собой законом Ома в операторной форме:

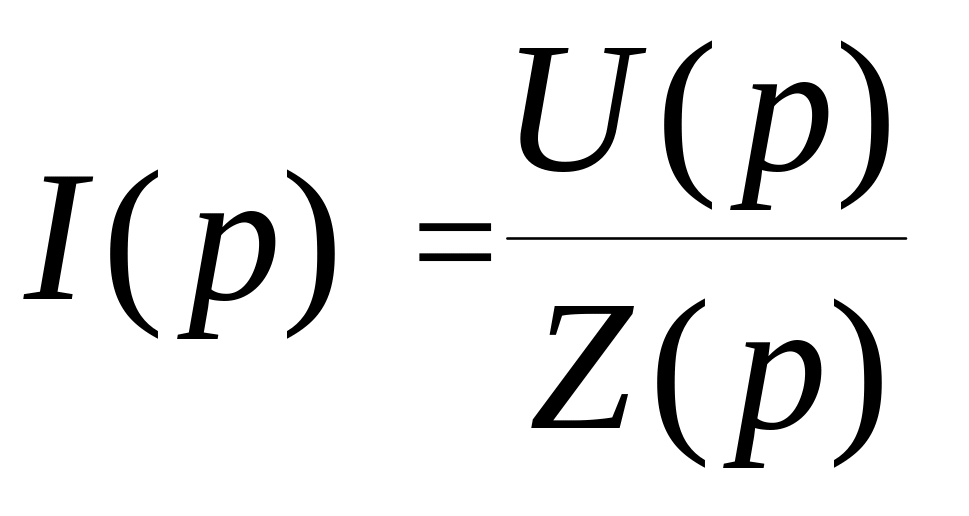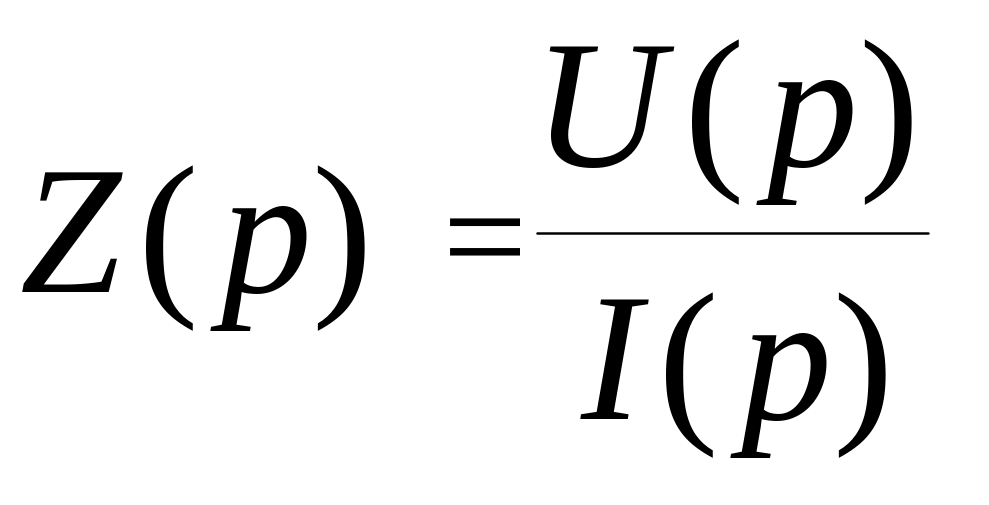или . (3.18)

Рассмотрим, как выражаются в операторной форме индуктивность, конденсатор и сопротивление. Для индуктивности известна следующая связь напряжения и тока:

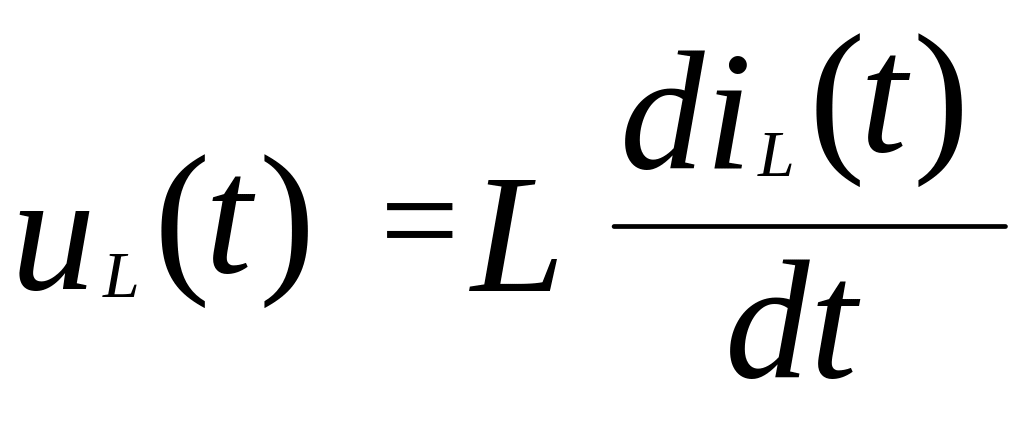. (3.19)

Переходя к операторному представлению напряжения и тока и пользуясь теоремой дифференцирования оригинала при нулевых начальных условиях, выражение (3.19) в операторной форме принимает вид:

.

По закону Ома находим сопротивление индуктивности в операторной форме:

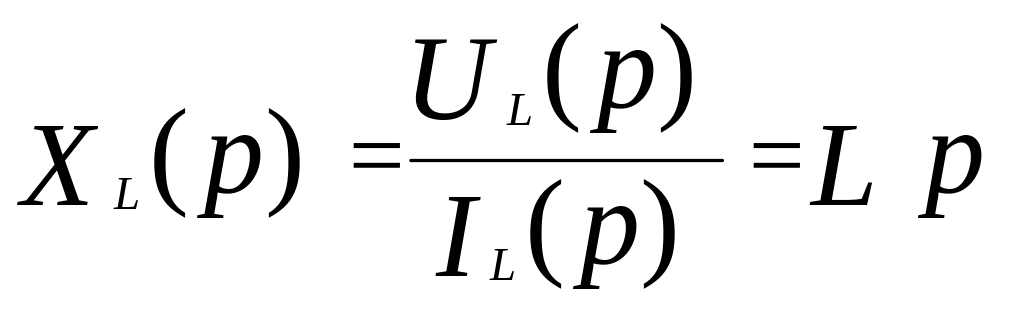. (3.20)

Для конденсатора связь между напряжением и током определяется соотношением:

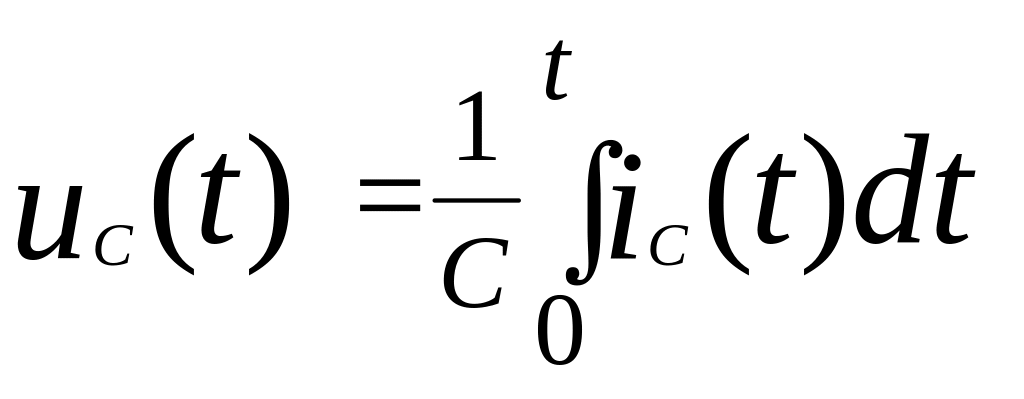. (3.21)

В операторной форме, с учетом теоремы интегрирования оригинала, соотношение (3.21) принимает вид:

.

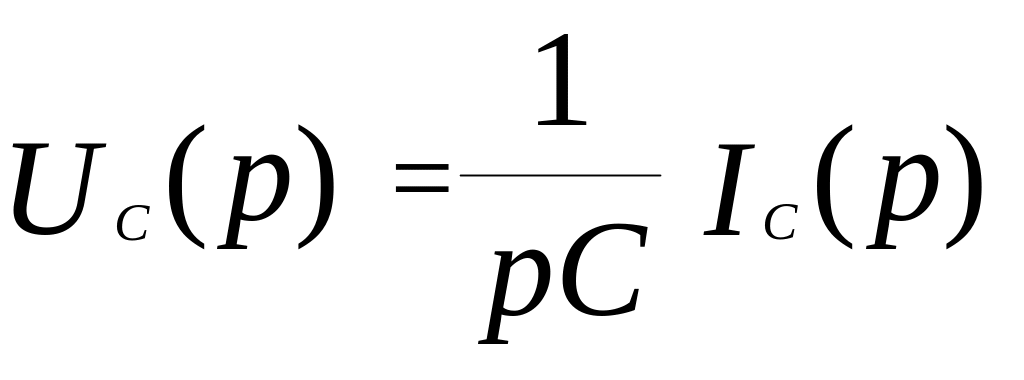Из последнего, с учетом (3.18), находим сопротивление конденсатора в операторной форме:

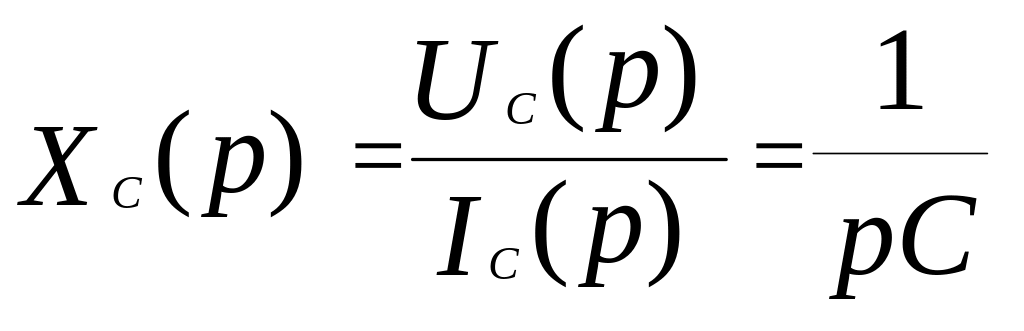. (3.22)

Для резистора связь между напряжением и током имеет вид:

.

Запишем в операторной форме это соотношение:

.

Отсюда, в соответствии с законом Ома, сопротивление резистора в операторной форме принимает вид:

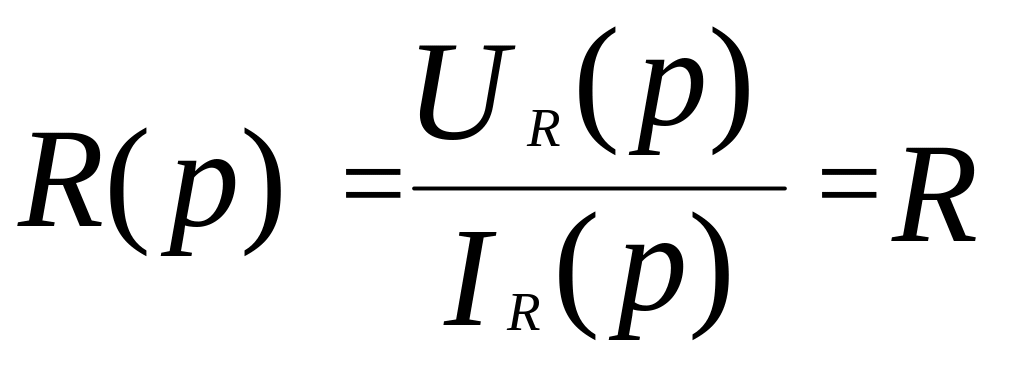. (3.23)

Законы Кирхгофа в операторной форме имеют вид аналогичный тому, как для цепей постоянного и переменного токов.

Первый закон Кирхгофа для узла цепи:

. (3.24)

Второй закон Кирхгофа для замкнутого контура:

. (3.25)

Последовательность расчета переходного процесса:

1. Исходная схема представляется в операторной форме, т. е. элементы исходной схемы заменяются на элементы, представленные в операторной форме;

2. Любым известным методом (методом эквивалентного преобразования, методом контурных токов, с помощью законов Кирхгофа, методом эквивалентного генератора и т. д.) находится операторное представление выходного напряжения;

3. По операторному представлению выходного напряжения (изображению выходного напряжения) находится оригинал выходного напряжения.

Рассмотрим применение данной последовательности расчета переходного процесса на примере схемы (рисунок 3.5). После замены элементов исходной схемы на элементы, представленные в операторной форме, схема принимает вид (рисунок 3.7).

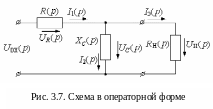
Запишем уравнения по первому и второму законам Кирхгофа:

. (3.26)

Выражаем напряжения и токи через параметры схемы:

,

,

,

, (3.27)

,

.

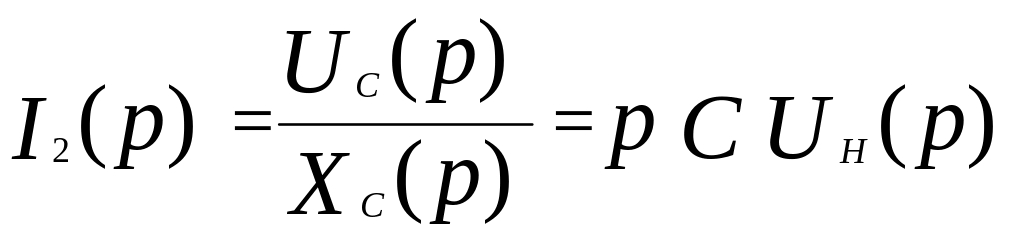Подставляя выражения для напряжений из (3.27) в систему (3.26), получим:

Пользуясь методом последовательного исключения, с учётом выражений для токов в (3.27), получаем:

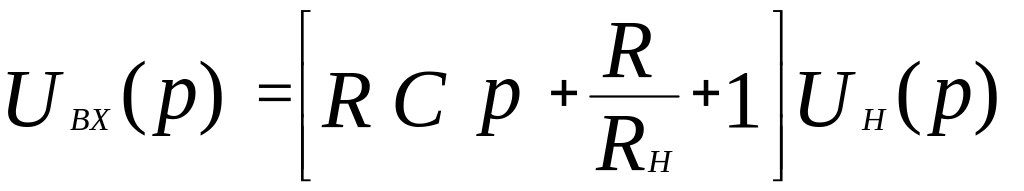. (3.28)

Подставляя в (3.28) выражение входного напряжения (3.1) в операторной форме:

,

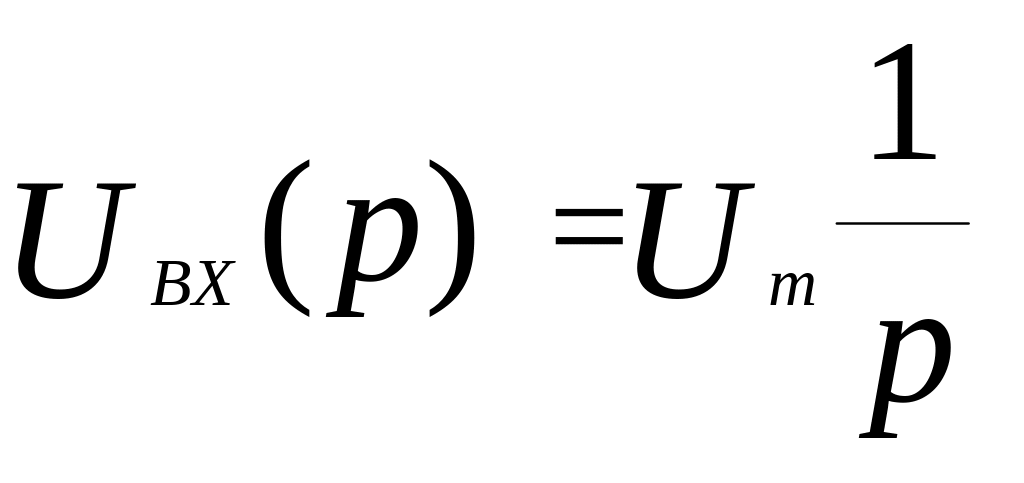находим изображение выходного напряжения:

, (3.29)

где , .

Выражение (3.29) полностью совпадает с выше полученным изображением выходного напряжения при рассмотрении примера первой последовательности применения преобразований Лапласа.

Рассмотренный способ интересен тем, что он позволяет применить для решения и метод эквивалентного преобразования. Объединяя R_Н(р) и Х_С(р) и обозначая эквивалентное сопротивление R_Н', получаем схему (рис. 3.8):

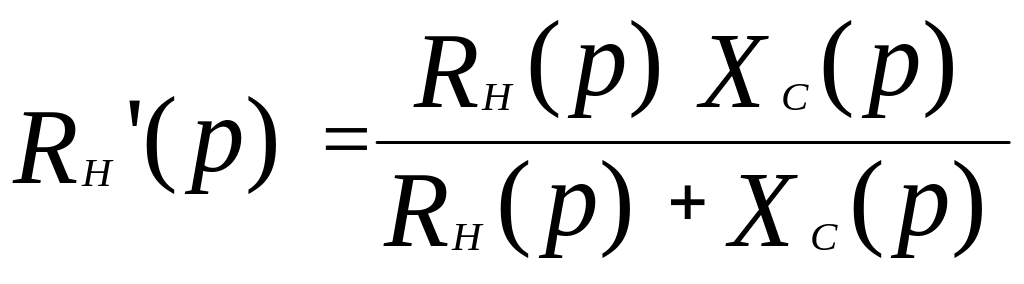. (3.30)

Из рис. 3.8 очевидно следующее решение:

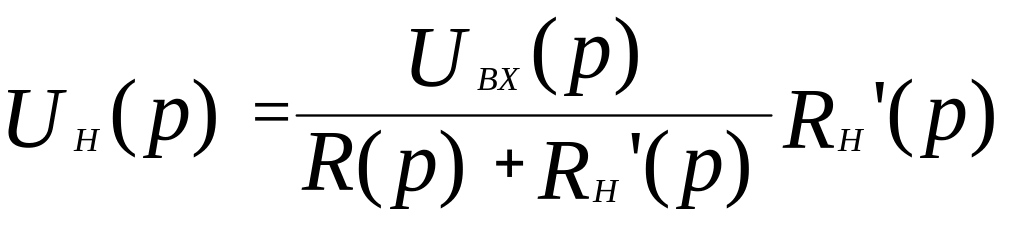(3.31)

Подставляя (3.30) в (3.31) и раскрывая значения R(р), R_Н(р), X_С(р) и U_ВХ(р), после простых преобразований получаем:

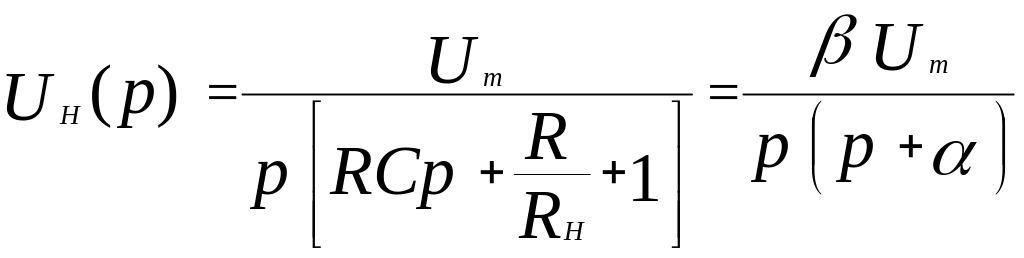, (3.32)

где , .

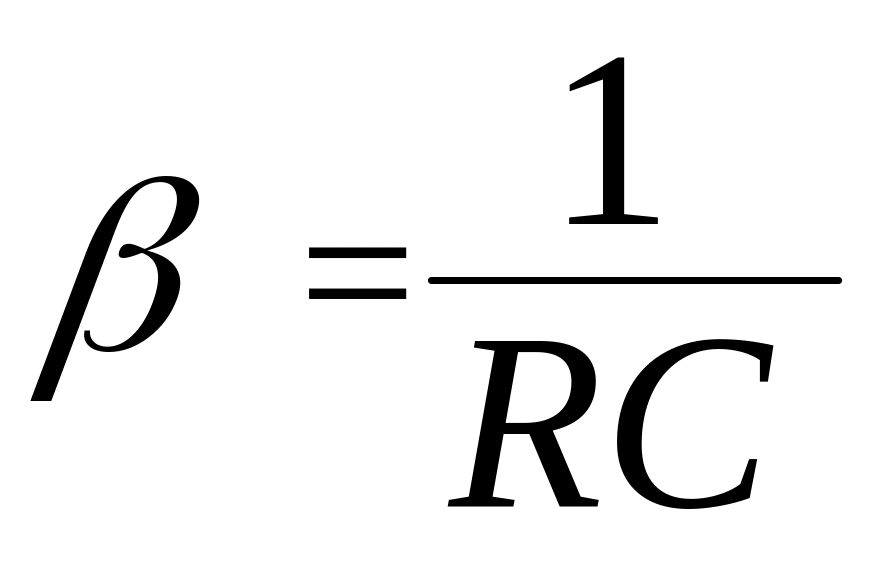Решение (3.32) совпадает с (3.29), но получено заметно меньшим числом действий, чем результат (3.29).

Для более сложной схемы можно применить метод эквивалентного генератора или метод контурных токов, которые уменьшают число расчетных действий по сравнению с получением решения методом законов Кирхгофа.

3.4. Переходный процесс в цепях первого порядка

Цепями первого порядка, как уже отмечалось, называются схемы, процессы в которых описываются дифференциальными уравнениями первого порядка. Такими являются схемы, содержащие реактивные элементы только одного типа - или индуктивности или конденсаторы. Помимо этих элементов в схеме присутствуют резисторы, которые не определяют порядок дифференциального уравнения схемы. Ниже будут рассмотрены схемы, состоящие из последовательно соединенных резистора и конденсатора (R-C цепь) или из последовательно соединенных резистора и индуктивности (R-L цепь). В зависимости от того, с какого элемента этих схем снимается выходной сигнал, эти схемы обладают различными функциональными свойствами.

3.4.1. Переходные процессы в RC и LR цепях, постоянная

времени цепи, условие интегрирования

Рассмотрим переходный процесс в RC-цепи (рисунок 3.9).

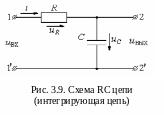
В дальнейшем будет показано, что при определенном соотношении величин R и C эта цепь осуществляет интегрирование входного сигнала. Поэтому такие схемы обычно называют интегрирующими.

На вход цепи подается сигнал ступенчатой формы (рис. 3.1)

.

Рассматриваем процессы в цепи при нулевых начальных условиях:

.

Найдем дифференциальное уравнение, связывающее выходное напряжение с входным. В соответствии со вторым законом Кирхгофа запишем уравнение:

.

Из схемы видно, что:

, , .

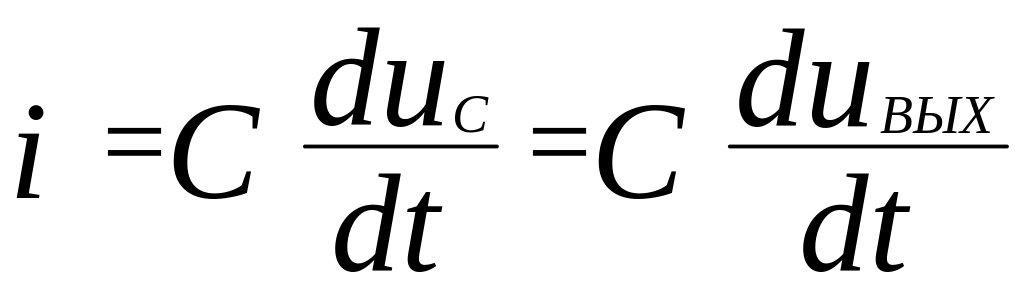С учетом этих соотношений исходное уравнение принимает вид:

.

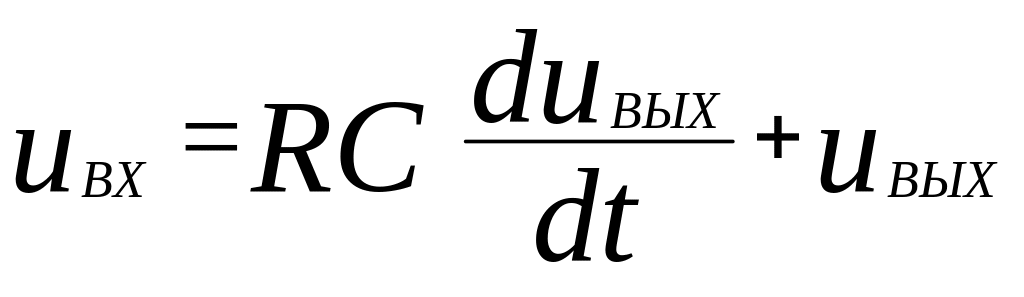При анализе переходных процессов используется понятие постоянной времени цепи , которое для данной цепи имеет вид:

. (3.33)

Через размерности R и C покажем, что  имеет размерность времени:

.

Тогда полученное уравнение можно записать так:

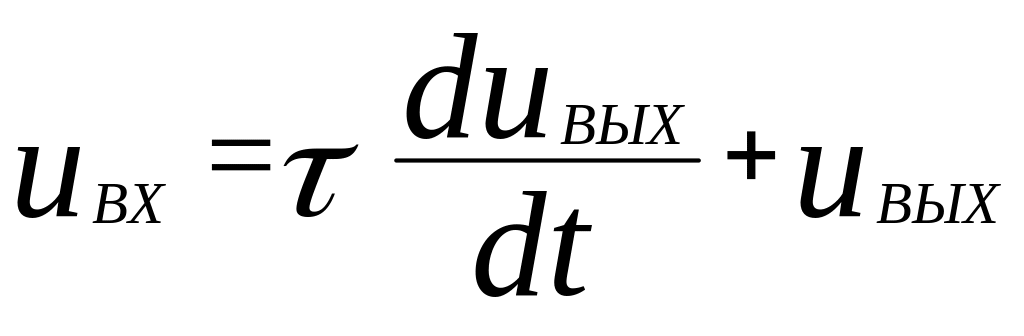. (3.34)

Применим преобразование Лапласа к анализу переходного процесса в рассмотренной схеме. Воспользуемся первым методом. Преобразуем по Лапласу дифференциальное уравнение (3.34):

.

Подставляя в это уравнение операторное представление входного сигнала (3.1):

,

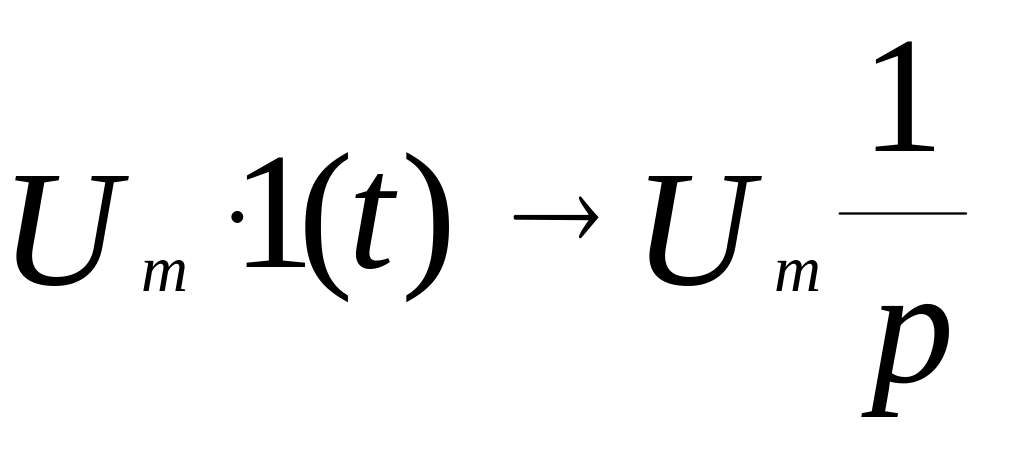находим решение в операторной форме:

.

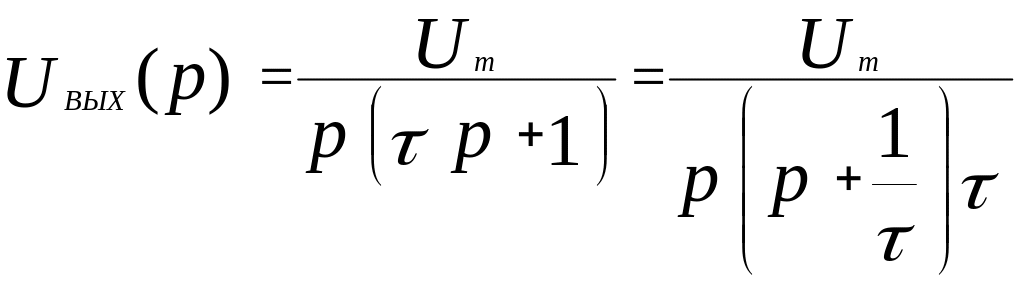Обращаясь к таблицам изображения и оригинала по Лапласу (Приложение 1), находим оригинал выражения для выходного напряжения:

. (3.35)

Рассмотрим поведение выходного напряжения (3.35) при изменении t. Значения t будем брать кратными :

,

где n – числа натурального ряда.

В таблице 3.1 представлены результаты вычислений (3.35):

Таблица 3.1.

t	0	1	2	3	4	5	∞
uВЫХ	0	0,632Um	0,865Um	0,950Um	0,982Um	0,993Um	Um

Н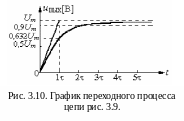 а рис. 3.10 по результатам вычислений показано изменение выходного напряжения во времени.

Теоретически время переходного процесса равно бесконечности. Практически принято считать, что переходный процесс закончен, если значение функции будет отличаться от установившегося значения не более чем на 10 %. Значит, переходный процесс можно считать установившимся, если выполняется условие:

.

Из графика видно, что переходный процесс можно считать установившимся по прошествии времени (3-4) .

.

Очевидно, чем меньше , тем меньше время переходного процесса. Из таблицы и из графика видно, что постоянная времени () равна времени в течение которого выходное напряжение примет значение равное 0,632U_m. Это позволяет определить  по виду переходного процесса.

Постоянную времени можно определить, проводя касательную из начала координат до пересечения с уровнем установившегося значения. Время до пересечения касательной с уровнем установившегося значения равно постоянной времени цепи . Действительно, взяв производную от (3.35) при t=0, находим:

.

Тогда уравнение касательной имеет вид:

.

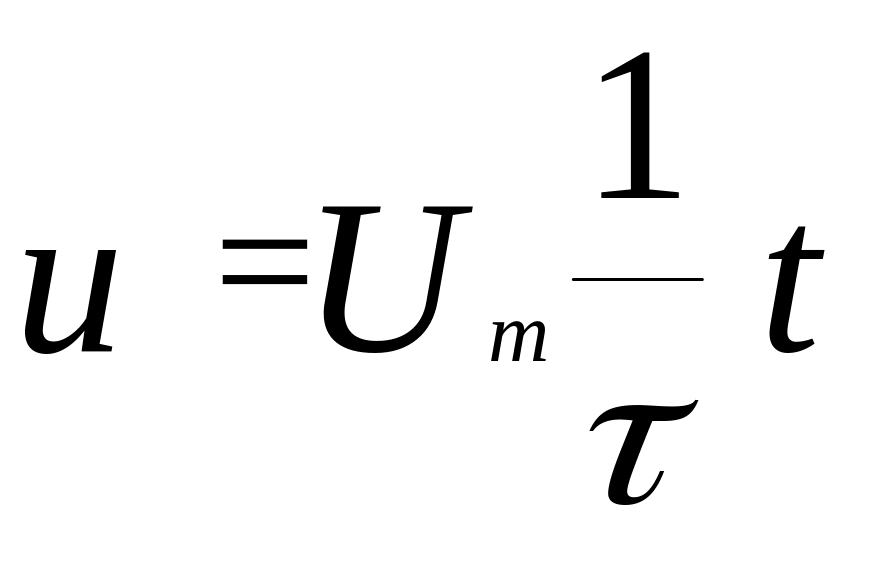Приравнивая последнее выражение к установившемуся значению выходного напряжения, определяем искомое время:

; .

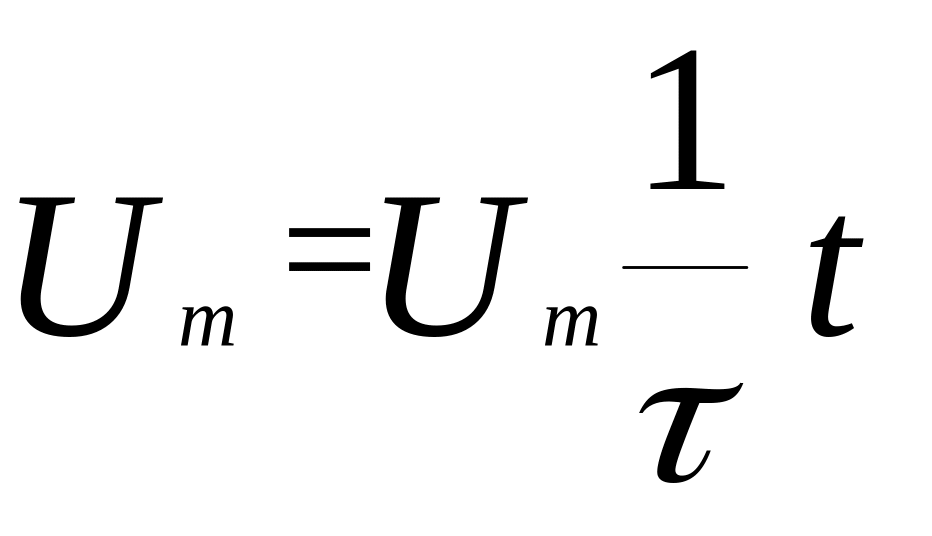Рассмотрим интегрирующие свойства цепи рис. 3.9. В интервале времени 0 < t <  значение выходного напряжения меньше его производной. При значительном  на этом интервале в уравнении (3.34) вторым слагаемым можно пренебречь. Тогда (3.34) принимает вид:

.

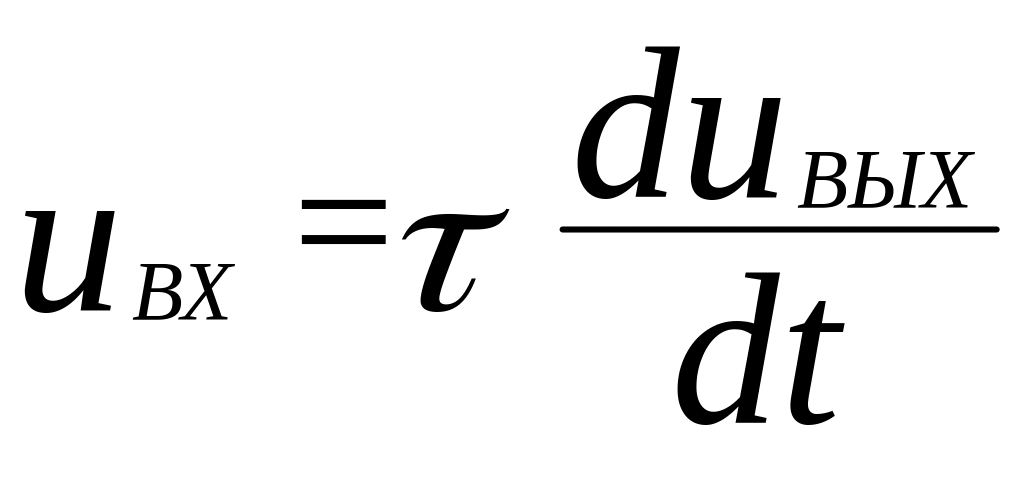Интегрируя это уравнение, получаем:

. (3.36)

Из (3.36) видно, что в начальном интервале переходного процесса и при большом значении  цепь рис. 3.9 обладает интегрирующими свойствами.

Сопротивление конденсатора в переходном режиме не остаётся постоянным, а изменяется во времени. Покажем это. Из (3.35) определяем ток через конденсатор:

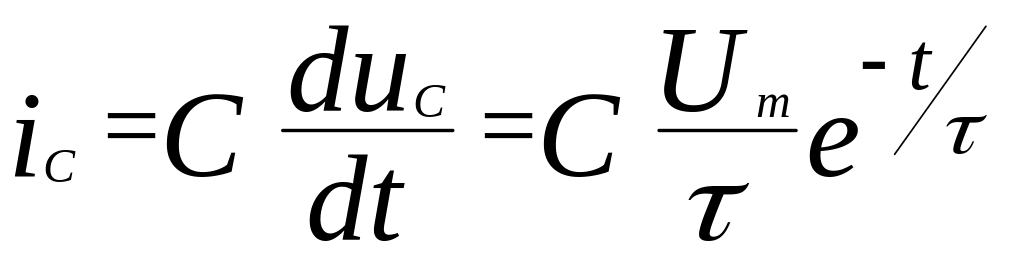. (3.37)

Используя (3.35) и (3.37), сопротивление конденсатора определяем по закону Ома:

. (3.38)

Из (3.38) следует, что в начальный момент времени (t = 0) сопротивление конденсатора равно нулю. Это полностью совпадает со следствием из закона коммутации для конденсатора.

В установившемся режиме, то есть при t =  сопротивление конденсатора равно бесконечности:

(3.39)

Итак, сопротивление конденсатора в установившемся режиме равно бесконечности, т. е. конденсатор при t= представляет собой разрыв.

Рассмотрим цепь, состоящую из последовательно соединенных индуктивности и резистора (рис. 3.11).

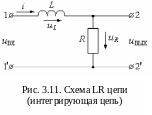
Запишем для нее уравнение по второму закону Кирхгофа:

.

С учетом следующих очевидных соотношений:

, , ,

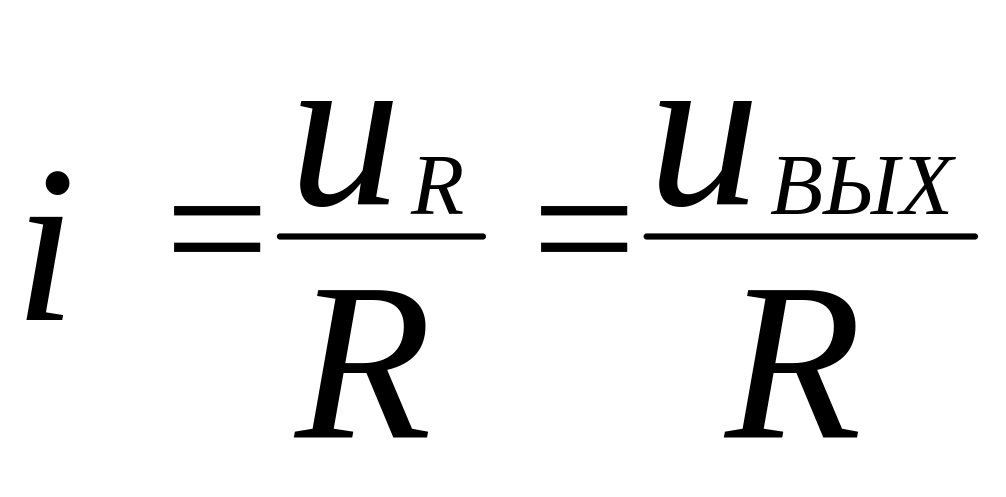это уравнение принимает вид:

.

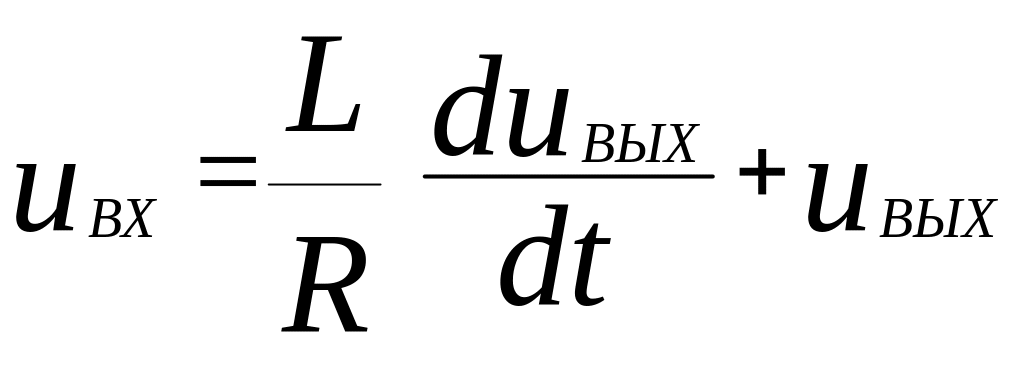Постоянная времени этой цепи равна:

.

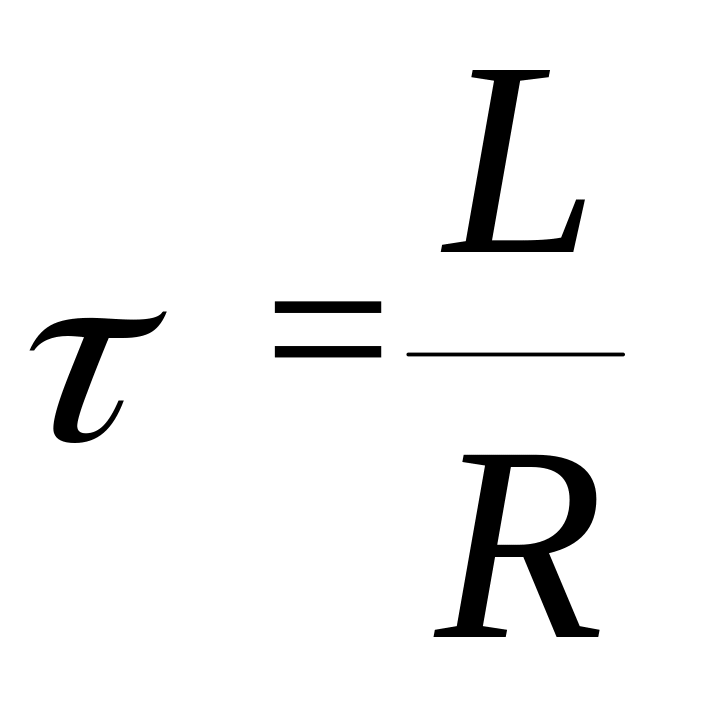Дифференциальное уравнение для рассматриваемой схемы принимает вид:

. (3.40)

Уравнение (3.40) полностью совпадает с уравнением (3.34). Это значит, что схема рис. 3.11 обладает теми же свойствами, что и схема рис. 3.9, а именно – её переходный процесс описывается формулой (3.35), и при значительном  эта цепь является так же интегрирующей.

О бщее свойство этих цепей (рис. 3.9 и рис. 3.11) еще состоит в том, что величина постоянной времени  влияет на длительность времени переходного процесса. На рис.3.12 показаны графики переходных процессов при различных значениях постоянной времени.

Видно, что с увеличением  увеличивается длительность переходного процесса. Это можно показать аналитически, если считать, что переходный процесс заканчивается при выполнении условия:

.

С учётом этого, из выражения (3.35) следует:

.

Решая это уравнение относительно времени t, получим:

, .

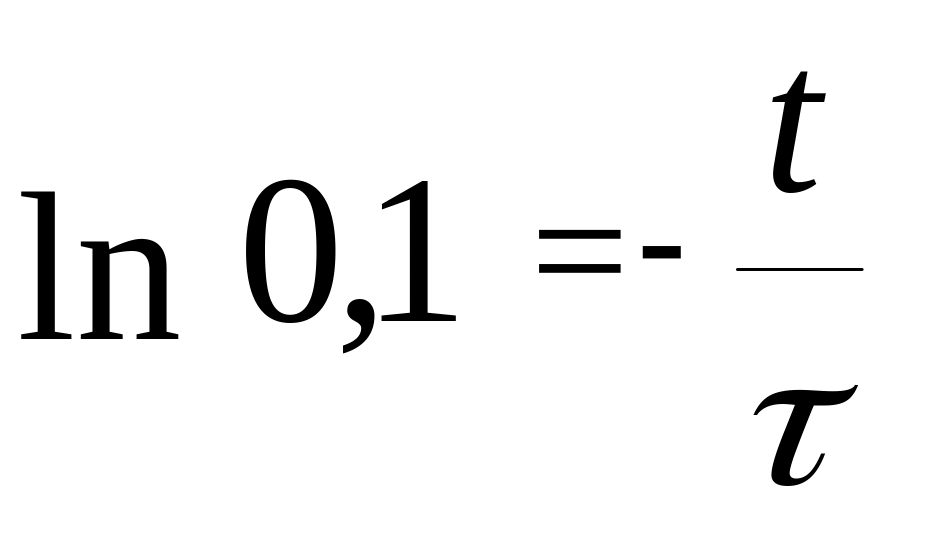Действительно, увеличение постоянной времени схемы ведёт к увеличению времени переходного процесса.

3.4.2. Переходные процессы в CR и RL цепях, условие дифференцирования

Р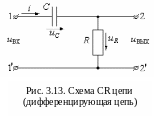 ассмотрим цепь, представленную на рис. 3.13. При определённом соотношении между величинами конденсатора и резистора эта схема обладает дифференцирующими свойствами.

Запишем для этой схемы уравнение по второму закону Кирхгофа:

.

Учитывая, что:

, , ,

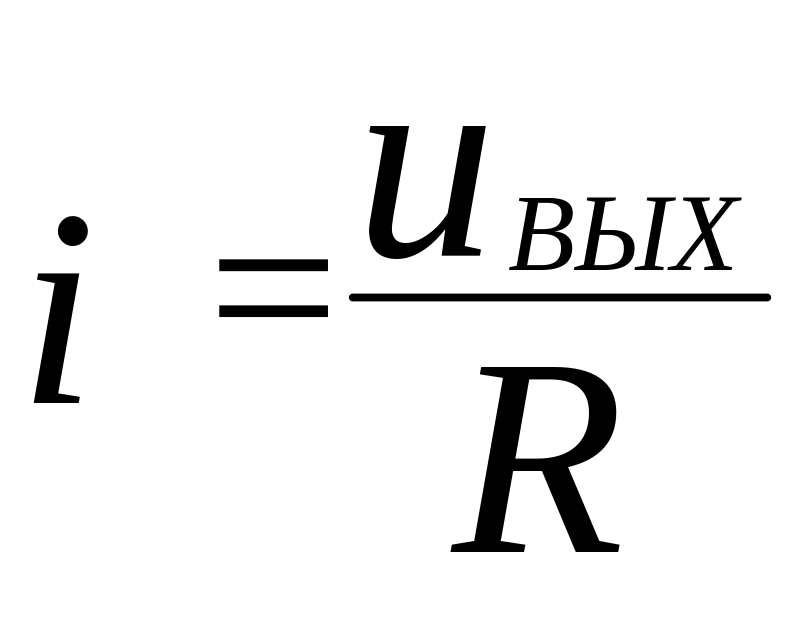исходное уравнение принимает вид:

.

В этом уравнении воспользуемся понятием постоянной времени  (3.33):

. (3.41)

Преобразуем уравнение (3.41) по Лапласу, учитывая, что входное напряжение имеет вид (3.1):

.

Решая это уравнение, находим операторное представление выходного напряжения:

.

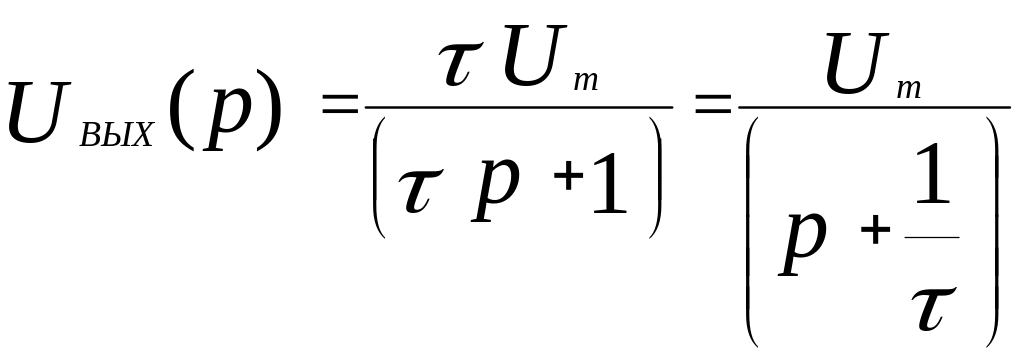Обращаясь к табличному представлению преобразований Лапласа (Приложение 1) находим оригинал выходного напряжения:

. (3.42)

На рис. 3.14 показано изменение выходного напряжения цепи рис. 3.13 во времени.

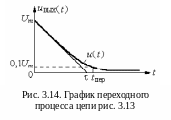
Как отмечалось, теоретически время переходного процесса равно бесконечности t_ПЕР=. На практике время переходного процесса в рассматриваемом случае (рис.3.14) равно моменту, когда выходное напряжение принимает значение, равное и меньшее 0.1 от максимального значения.

Постоянную времени, определяемую известным соотношением (=RC), можно также определить из графика переходного процесса (рис. 3.14). Для этого необходимо провести касательную к кривой переходного процесса при t=0 и продолжить ее до пересечения с осью времени. Точка пересечения даст значение . Это легко доказать. Определяя производную от (3.42) при t=0:

,

находим уравнение касательной:

.

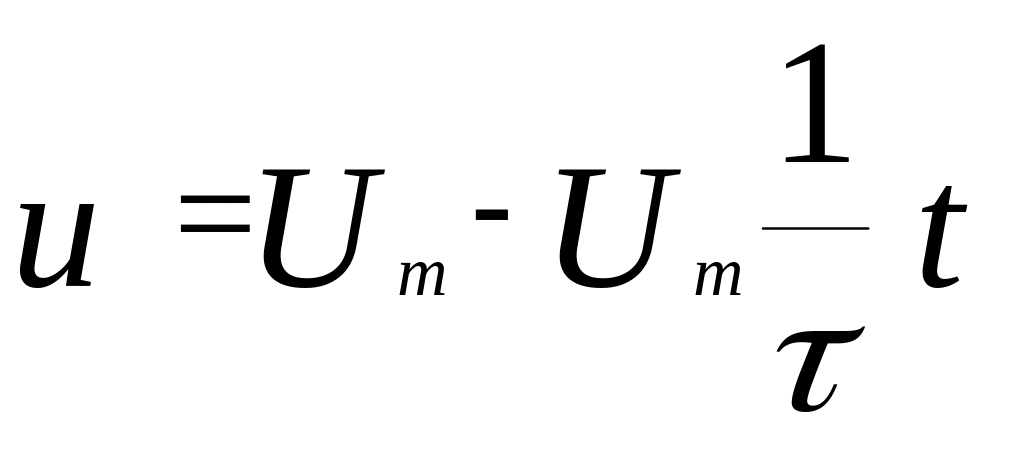Отсюда находим время при котором u=0, т. е. произойдет пересечение касательной с осью времени:

,

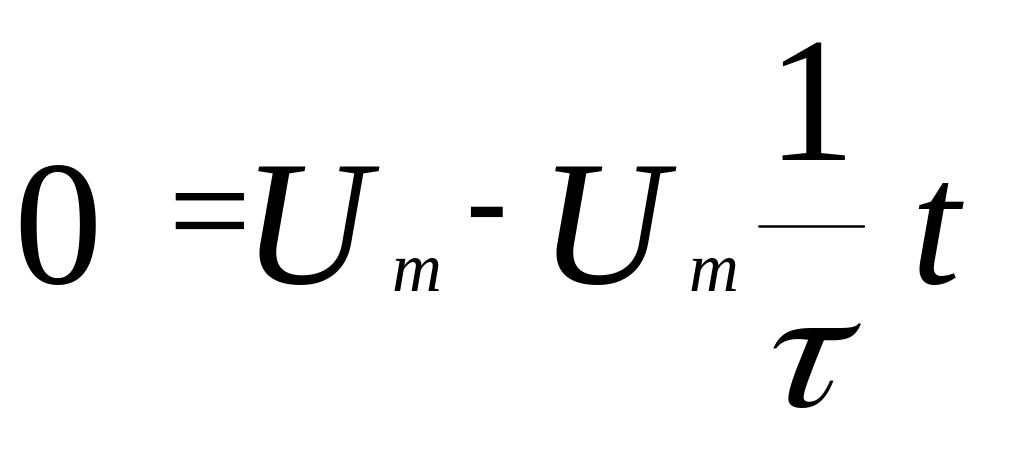Рассмотрим цепь из последовательно соединенных резистора и индуктивности (рис. 3.15).

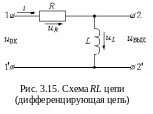
Составляем уравнение по второму закону Кирхгофа:

,

которое с учетом того, что:

, , ,

принимает вид:

.

Как отмечалось, для индуктивно-резистивной цепи постоянная времени равна:

.

С учетом понятия постоянной времени, уравнение для схемы рис. 3.15 принимает окончательный вид:

. (3.43)

Уравнение (3.43) полностью совпадает с уравнением (3.41). Поэтому все результаты, которые были получены для схемы рис.3.13, таки как - решение (3.42), график переходного процесса (рис. 3.14), полностью соответствуют и для схемы рис. 3.15.

При определенных соотношениях рассмотренные схемы (рис.3.13 и рис.3.15) могут выполнять операцию дифференцирования над входным сигналом. Так, если <<1, то в уравнениях (3.41) и (3.43) второе слагаемое будет много меньше первого и им можно пренебречь. Тогда эти уравнения принимают вид:

.

После дифференцирования последнего уравнения получим:

.

Условие, при котором <<1 легко реализуется на практике. Так, если взять R=1 кОм, С=10^-6 Ф=1 мкФ, то величина  равна:

[С]<<1.

В рассмотренных схемах (рис. 3.13 и рис.3.15) величина  влияет на длительность переходного процесса (рис. 3.16).

Э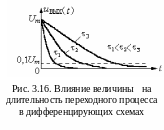 то видно из графиков, но это можно показать аналитически, если считать переходный процесс законченным, когда

.

С учётом этого, из выражения (3.42) следует:

.

Решая это уравнение относительно t, находим время переходного процесса:

, .

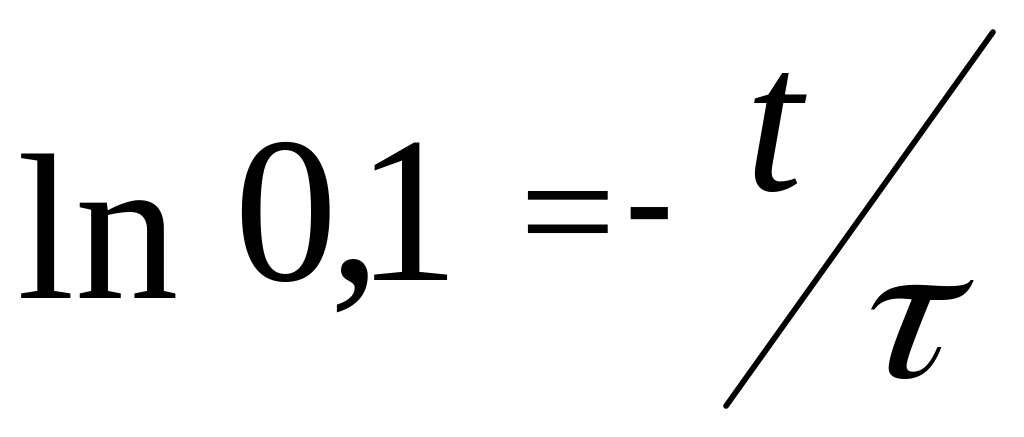Действительно, увеличение постоянной времени цепи приводит к увеличению времени переходного процесса.

Сопротивление катушки индуктивности в переходном режиме не остаётся постоянным, а изменяется во времени. Покажем это.

В соответствии с (3.42) напряжение на индуктивности определяется выражением:

.

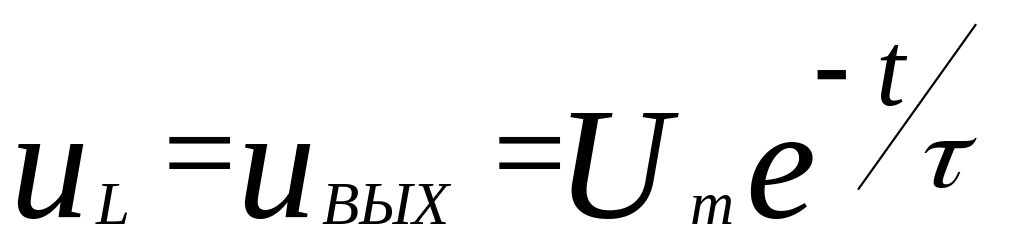Ток в индуктивности определяется следующим соотношением:

.

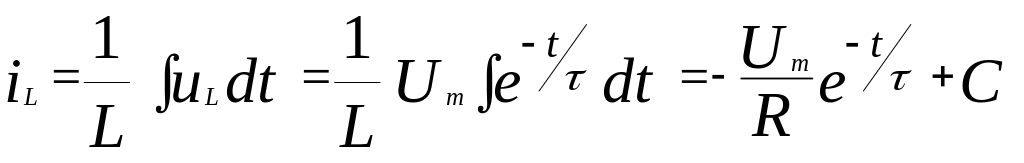Константа С определяется из условия нулевых начальных условий:

,

,

.

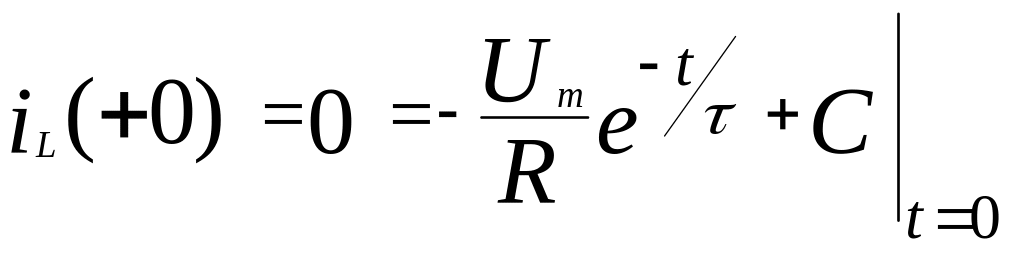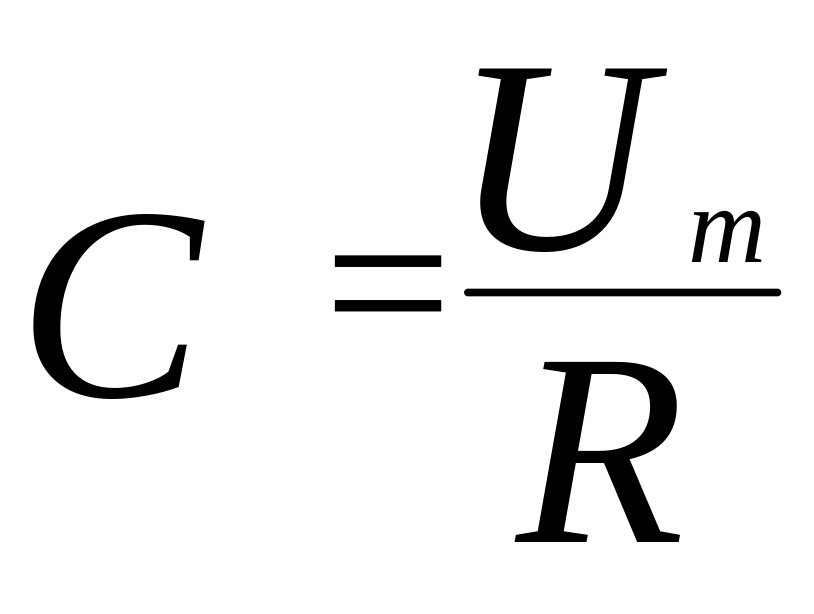С учетом найденного значения константы ток в индуктивности определяется выражением:

.

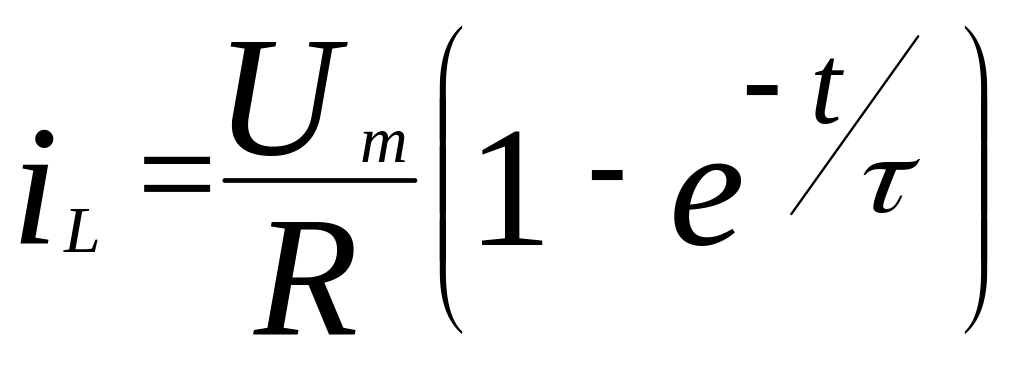Пользуясь законом Ома, определяем сопротивление катушки индуктивности:

.

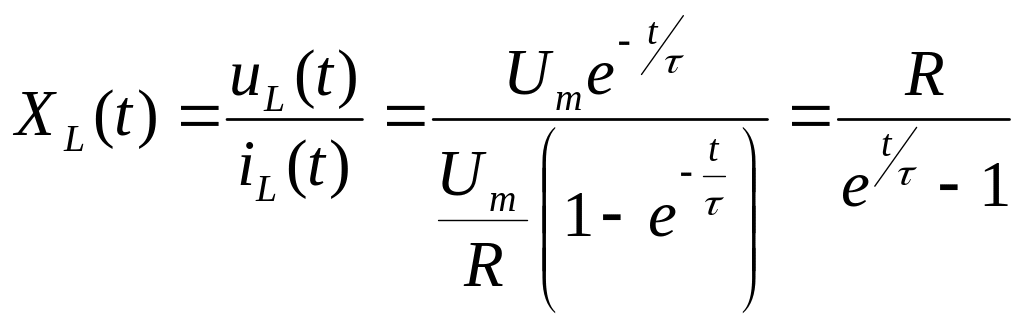Подставляя значение t = 0, находим величину сопротивления катушки индуктивности в начальный момент переходного процесса:

.

Этот результат полностью совпадает с результатом следствия из закона коммутации для индуктивности (раздел 3.2).

Подставляя значение t = ∞ , находим величину сопротивления катушки индуктивности в установившемся режиме:

.

Сопротивление индуктивности в установившемся режиме равно нулю, т. е. индуктивность в установившемся режиме представляет собой короткое замыкание.

3.5. Переходные процессы в цепях второго порядка

Переходный процесс в цепях второго порядка рассмотрим на примере схемы рис. 3.17. Как отмечалось выше, в цепях второго порядка присутствуют два типа энергоёмких элемента – катушка индуктивности и конденсатор.

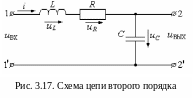
Как отмечалось, переходный процесс в этой цепи задается ступенчатым входным воздействием (3.1). Анализ переходного процесса состоит в рассмотрении изменения выходного напряжения во времени при ступенчатом входном воздействии. Для этого необходимо получить дифференциальное уравнение, связывающее выходное напряжение с входным и решить его. Запишем уравнение по второму закону Кирхгофа:

. (3.44)

Выразим все напряжения в правой части уравнения через выходное напряжение. Предварительно рассмотрим следующие очевидные соотношения.

, ,

, .

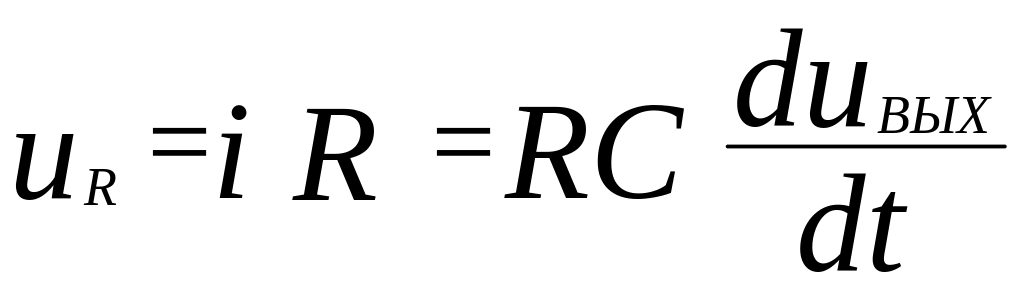С учетом этих соотношений исходное уравнение (3.44) принимает вид:

.

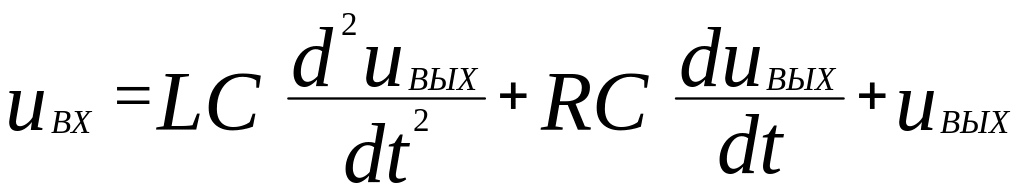Запишем это уравнение в приведенной форме

. (3.45)

Для удобства дальнейшего анализа введем обозначения:

, .

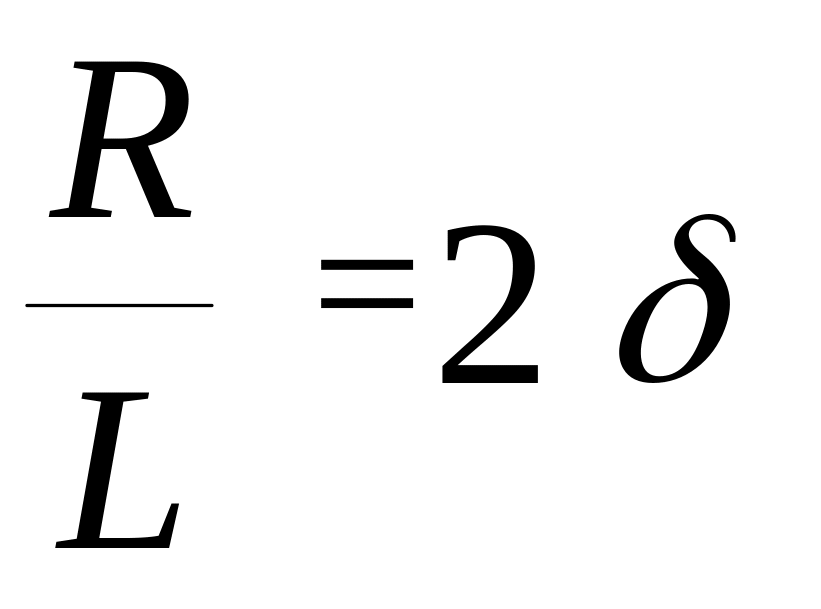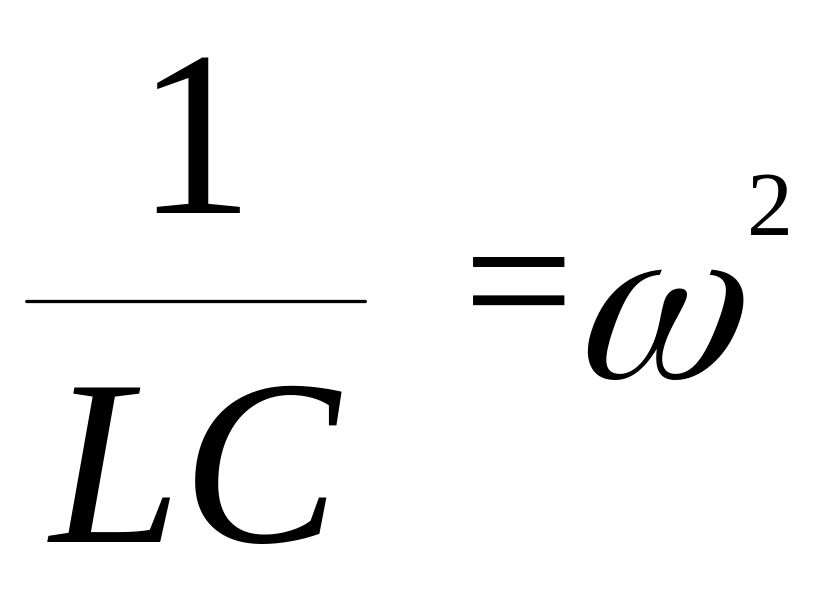Коэффициент при первой производной (2) уравнения (3.45) отображает диссипативные свойства цепи, так как только он содержит диссипативный элемент схемы. Коэффициент при свободном члене (²) равен квадрату резонансной частоты схемы, что видно из соотношения. С учетом этих обозначений уравнение (3.45) принимает вид:

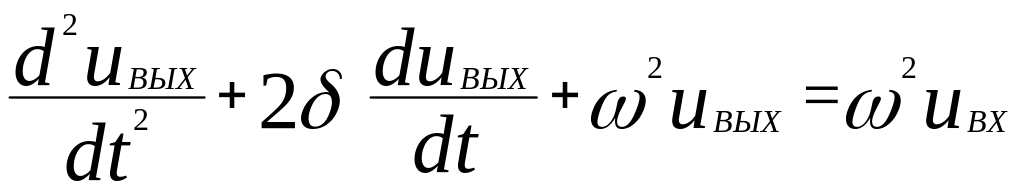. (3.46)

Решение этого уравнения будем искать с помощью преобразований Лапласа. Преобразуя по Лапласу это уравнение, получим:

.

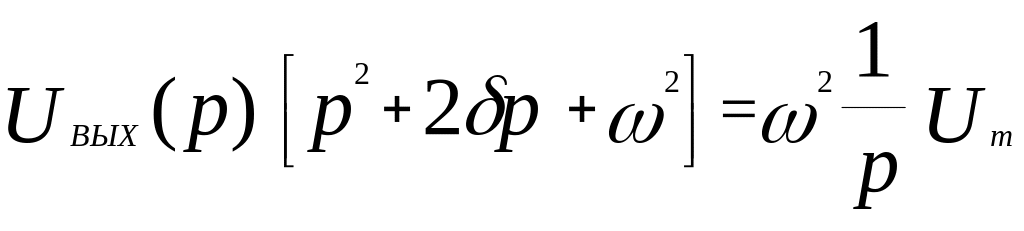Из этого уравнения находим операторное представление (изображение) выходного напряжения:

. (3.47)

Из теории преобразований Лапласа известно, что знаменатель выражения (3.47), приравненный к нулю, называется характеристическим уравнением:

. (3.48)

Решая (3.48), находим три корня характеристического уравнения:

, . (3.49)

Решение (3.47) выразим через корни характеристического уравнения:

. (3.50)

Оригинал решения можно найти следующими способами. Если корни характеристического уравнения вещественные, то можно воспользоваться таблицей прямого и обратного преобразования Лапласа (Приложение 1). В случае громоздкости выражения изображения, его можно упростить, пользуясь методом разложения дробей на простые дроби и представить в виде простых дробей, имеющих место в названной таблице.

При комплексно – сопряжённых корнях характеристического уравнения определение оригинала следует произвести с помощью вычетов.

Рассмотрим случай, когда корни характеристического уравнения вещественные и разные. Приведём полученное изображение решения (3.50) к табличному виду. Для этого корни характеристического уравнения обозначим так:

, ,

Тогда решение (3.50) можно записать в следующем виде:

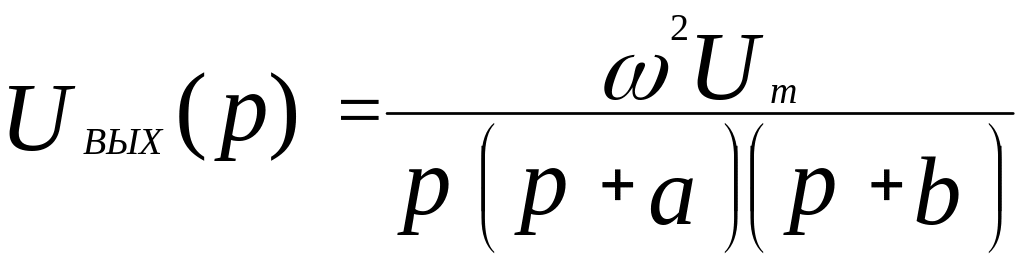. (3.51)

Обращаясь к таблице преобразований Лапласа, находим оригинал искомого напряжения, который имеет вид:

. (3.52)

Найдём значение напряжения в начальный момент времени, то есть при . Подставляем это значение времени в (3.52) и находим:

.

Найдём значение напряжения в установившемся режиме, то есть при . Подставляем это значение времени в (3.52) и находим:

.

Найдём:

.

С учётом полученного, определяем окончательно значение выходного напряжения в установившемся режиме:

.

И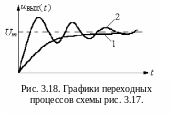 з (3.52) видно, что переходный процесс имеет экспоненциальный характер, выходит из нулевого значения и стремится к . На рис. 3.18 этому переходному процессу соответствует график 1.

Если в решении корней P_1,2 будет выполняться условие ² > ², то эти корни будут комплексно-сопряженными. В этом случае переходный процесс будет иметь колебательный характер (рис. 3.18, кривая 2).

Состояние схемы (рис. 3.17) в начальный момент (t=0) и в установившемся режиме (t=) можно определить много проще, без составления дифференциального уравнения и его решения, что в инженерной практике является важным. Для определения значения напряжения в начальный момент времени необходимо воспользоваться следствиями из законов коммутации (раздел 3.2), в соответствии с которыми в момент коммутации индуктивность имеет сопротивление равное бесконечности, а сопротивление конденсатора равно нулю. В соответствии с этим необходимо в исходной схеме индуктивность заменить разрывом цепи, а конденсатор заменить перемычкой. Схема замещения исходной схемы (рис. 3.17) на её вид в начальный момент времени представлена на рис.3.19(а). Из неё видно, что в начальный момент времени напряжение на её выходе будет равно нулю.

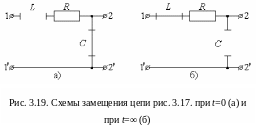
Для определения значения напряжения в установившемся режиме необходимо воспользоваться рассмотренными в разделах 3.4.1 и 3.4.2 свойствами конденсатора и индуктивности в установившемся режиме. Они состоят в том, в установившемся режиме сопротивление конденсатора равно бесконечности, а сопротивление индуктивности равно нулю. В соответствии с этими свойствами необходимо в исходной схеме конденсатор заменить разрывом цепи, а катушку индуктивности перемычкой. Схема замещения исходной схемы (рис. 3.17) на её вид в установившемся режиме представлена на рис.3.19(б). Из неё видно, что в установившемся режиме напряжение на её выходе будет равно величине входного напряжения.

3.6. Контрольные вопросы

Для проверки степени усвоения материалов главы 3 рекомендуется ответить на ниже предлагаемые вопросы. Свои ответы сравните с ответами, приведёнными в конце этих вопросов.

1. Переходные процессы имеют место в цепи, содержащей хотя бы один ……… элемент.

А. Резистивный. Б. Реактивный.

2. Какое из соотношений отображает закон коммутации для индуктивности?

А. i(-0) = i(+0). Б. U(-0) = U(+0).

3. Какое из соотношений отображает закон коммутации для конденсатора?

А. i(-0) = i(+0). Б. U(-0) = U(+0).

4. Укажите последовательность действий при анализе переходного процесса с помощью преобразований Лапласа (первая последовательность).

А. Находится искомая величина в операторном виде.

Б. Составляется обобщённое дифференциальное уравнение цепи.

В. Находится оригинал решения.

Г. Обобщённое дифференциальное уравнение представляется в операторной форме.

5. Укажите последовательность действий при анализе переходного процесса с помощью преобразований Лапласа (вторая последовательность).

А. Преобразуются по Лапласу исходные уравнения, полученные с помощью законов Кирхгофа.

Б. Находится решение в операторной форме.

В. Записываются исходные уравнения в оригинале, полученные с помощью законов Кирхгофа.

Г. Находится обобщённое уравнение в операторной форме.

Д. Определяется оригинал решения.

6. Укажите последовательность действий при анализе переходного процесса с помощью преобразований Лапласа (третья последовательность).

А. Записываются исходные уравнения в операторной форме.

Б. Находится решение в операторной форме.

В. Элементы схемы представляются в операторной форме.

Г. Определяется оригинал решения.

7. В момент коммутации при нулевых начальных условиях сопротивление катушки индуктивности равно ………

А. Нулю. Б. Бесконечности.

8. В момент коммутации при нулевых начальных условиях сопротивление конденсатора равно ………

А. Нулю. Б. Бесконечности.

9. Какое из соотношений справедливо для определения постоянной времени в

RC - цепи ?

А. , Б. , В. .

10. Какое из соотношений справедливо для определения постоянной времени в

RL – цепи ?

А. , Б. , В. .

11. Сопротивление конденсатора в установившемся режиме равно …………

А. Нулю. Б. Бесконечности.

12. RC – цепь обладает интегрирующими свойствами, если постоянная времени ……………

А. Мала. Б. Велика.

13. CR – цепь обладает дифференцирующими свойствами, если постоянная времени …………..

А. Мала. Б. Велика.

14. Сопротивление катушки индуктивности в установившемся режиме переходного процесса равно ……….

А. Нулю. Б. Бесконечности.

15. Переходный процесс в цепях второго порядка имеет асимптотический вид, если корни характеристического уравнения ………

А. Вещественные. Б. Комплексные.

16. Переходный процесс в цепях второго порядка имеет колебательный вид, если корни характеристического уравнения ………

А. Вещественные. Б. Комплексные.

Правильные ответы:

1. Б. 2. А. 3. Б. 4. Б, Г, А, В. 5. В, А, Г, Б, Д. 6. В, А, Б, Г. 7. Б. 8.А. 9. В. 10. А. 11. Б. 12. Б. 13. А. 14. А. 15.А. 16.Б.