Свойства энтропии

1. Энтропия принимает значение, равное 0, только в случае детерминирован­ного источника сообщений системы.

Детерминированность источника означает, что один из возможных символов генерируется источником постоянно (с единичной вероятностью), а остальные – не производятся вовсе. Предположим для определенности, что генерируется k-й символ.

Пусть P(a_k)=1 , а P(a_i)=0 для всех i=1,m ik

Тогда, обозначив элемент суммы в формуле (3.8) через h_i, получим

Раскроем неопределенность вида 0∙∞ по правилу Лопиталя.

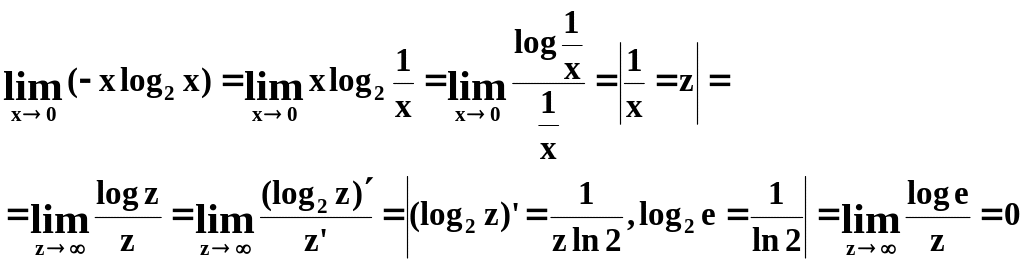
Следовательно, для детерминированного источника h_i= 0 для всех i. С другой стороны, если ни одна p(a_i)1, то ни одно слагаемое h_i не обращается в 0. Что и требовалось доказать.

2. Энтропия - величина неотрицательная и ограниченная.

Если каждое слагаемое h_i=-p(a_i)log₂p(a_i) неотрицательно и ограниченно, то и их сумма также будет неотрицательна и ограниченна.

Докажем неотрицательность:

p(a)  0; p(a) ≤ 1  log p(a) ≤ 0  - p(a) log p(a)  0

Докажем ограниченность, продифференцировав по p:

Следовательно, величина h_i имеет экстремум (можно доказать, что это максимум), а значит это величина ограниченная (см. рис.3.2)

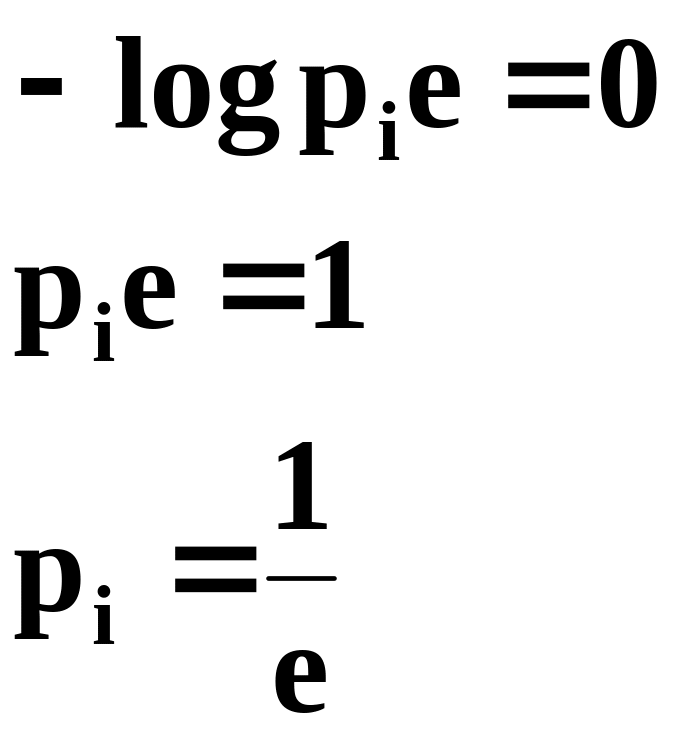
h _i

p_i

0 1/e 1

Рис. 3.2. К свойству ограниченности энтропии.

3. Энтропия системы, имеющей m равновероятных состояний, максимальна и равна log2m.

Докажем максимальность

Пусть m=2, тогда p₁+p₂=1

H = -p₁∙logp₁ - p₂∙logp₂ = -p₁∙logp₁-(1-p₁)∙log(1-p₁). Чтобы найти максимум энтропии, определим и приравняем нулю частную производную.

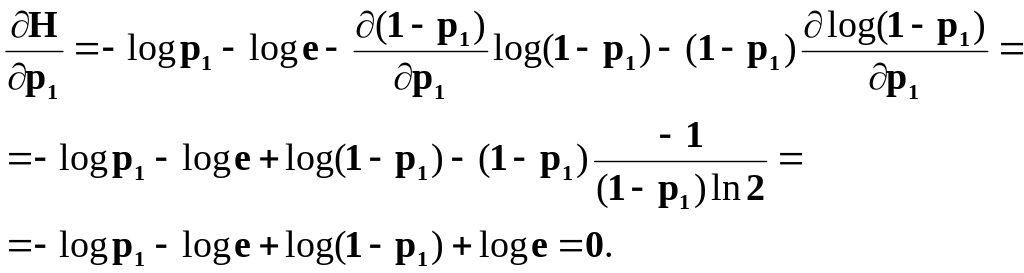
-log p₁ + log(1-p₁) = 0

p₁= ½ = p₂

Следовательно, при двух символах в алфавите максимум энтропии достигается в случае равновероятных символов. То же можно доказать и для большего числа символов в алфавите.

Найдем значение максимальной энтропии. Пусть все символы равновероятны: p_i = 1/m.

4. Совместная энтропия независимых источников сообщений равна сумме энтропий.

Пусть источник А порождает ансамбль Na сообщений (a₁, a₂,…, a_Na), источник B порождает ансамбль Nb сообщений (b₁, b₂,…, b_Nb) и источники независимы. Общий алфавит источников представляет собой множество пар вида (a_i, b_j), общая мощность алфавита равна NaNb.

Совместная энтропия композиции двух источников равна

Поскольку A и B независимы, то P(a_i,b_j) = P(a_i)∙P(b_j), a log P(a_i,b_j) = log P(a_i) + log P(b_j). Отсюда вытекает:

Изменим порядок суммирования

учитывая, что и , получим

(3.9)

Вывод можно распространить и на большее количество независимых источников

Условная энтропия

Найдем совместную энтропию сложной информационной системы (композиции A, B) в том случае, если их сообщения не являются независимыми, т.е. если на содержание сообщения B оказывает влияние сообщение A.

Например, сообщение «Спартак выиграл в футбольном матче против Динамо» полностью снимает неопределенность сообщения о том, как сыграло Динамо.

Другой пример: сообщение А содержит информацию о женщине (фамилию, имя, отчество, год рождения, место рождения, образование, домашние адрес и телефон), а сообщение В содержит аналогичную информацию о ее муже. Очевидно, что сообщение В частично содержит в себе информацию А (а именно: фамилию жены, ее домашний адрес и телефон, скорее всего совпадающие с фамилией, домашним адресом и телефоном мужа, а также вероятностную оценку ее года рождения, который скорее всего близок к году рождения мужа). Таким образом, совместная энтропия двух сообщений не является простой суммой энтропий отдельных сообщений.

Пусть источник А порождает ансамбль Na сообщений (a₁, a₂,…, a_Na), источник B порождает ансамбль Nb сообщений (b₁, b₂,…, b_Nb) и источники зависимы. Общий алфавит источников представляет собой множество пар вида (a_i, b_j), общая мощность алфавита: NaNb.

Энтропия сложной информационной системы (из двух источников) равна

Поскольку A и B зависимы, то P(a_i,b_j) = P(a_i)∙P(b_j|a_i),

a log P(a_i,b_j) = log P(a_i) + log P(b_j|a_i). Подставив это в выражение для энтропии сложной системы, получаем:

В первом слагаемом индекс j имеется только у B, изменив порядок суммирования, получим член вида: , который равен 1 поскольку характеризует достоверное событие (какое-либо сообщений b_j в любом случае реализуется). Следовательно, первое слагаемое оказывается равным:

Во втором слагаемом члены вида имеют смысл энтропии источника B при условии, что реализовалось сообщение a_i – будем называть ее частной условной энтропией. Если ввести данное понятие и использовать его обозначение, то второе слагаемое будет иметь вид:

, (3.10)

где H(B|A) есть общая условная энтропия источника В относительно источника А. Окончательно получаем для энтропии сложной системы:

H(A, B) = H(A) + H(B|A) (3.11)

Полученное выражение представляет собой общее правило нахождения энтропии сложной системы. Совершенно очевидно, что выражение (3.9) является частным случаем (3.11) при условии независимости источников А и В.

Относительно условной энтропии можно высказать следующие утверждения:

1. Условная энтропия является величиной неотрицательной. Причем H(B|A) = 0 только в том случае, если любое сообщение А полностью определяет сообщение В, т.е.

H(B|a₁) = H(B|a₂) =…= H(B|a_N) = 0

В этом случае H(А,B) = H(A).

2. Если источники А и В независимы, то H(B|A) = H(B), причем это оказывается наибольшим значением условной энтропии. Другими словами, сообщение источника А не может повысить неопределенность сообщения источника В; оно может либо не оказать никакого влияния (если источники независимы), либо понизить энтропию В.

Приведенные утверждения можно объединить одним неравенством:

0 ≤ H(B|A) ≤ H(B), (3.12)

т.е. условная энтропия не превосходит безусловную.

3. Из соотношений (3.11) и (3.12) следует, что

H(A, B) ≤ H(A) + H(B),

причем равенство реализуется только в том случае, если источники А и В независимы.