
- •Лабораторная работа № 4 построение ЭмпирическиХ формул
- •Содержание работы
- •Основные понятия
- •Этапы построения эмпирических формул
- •На основании точечного графика, построенного по экспериментальным данным, выдвигается гипотеза относительно вида аппроксимирующей функции.
- •Этап 2. Определение параметров эмпирической формулы
- •Метод наименьших квадратов
- •Общее решение задачи на примере аппроксимирующей функции с тремя параметрами.
- •Линейная зависимость
- •Квазилинейная зависимость (нелинейная двухпараметрическая)
- •1. Гипербола .
- •Квадратичная зависимость (трехпараметрическая)
- •Постановка задачи
- •Варианты заданий
- •Содержание отчёта
- •Вопросы и задания для самоконтроля
- •Идея построения формул
- •Квадратурные формулы прямоугольников
- •Применение интерполяционного полинома Лагранжа для интегрирования
- •Квадратурные формулы Ньютона–Котеса Пусть , .
- •Формула трапеций (при )
- •Формула Симпсона (при )
- •Квадратурная формула Чебышева
- •Квадратурная формула Гаусса
- •Предварительная информация
- •Вывод формулы
- •Постановка задачи Необходимо:
- •Вычислить определенный интеграл , используя квадратурную формулу:
- •Варианты заданий
- •Лабораторная работа № 6
- •Содержание работы
- •Решение оду первого порядка
- •Метод Эйлера
- •У точненный метод Эйлера
- •Методы Рунге Кутта
- •Построение методов
- •Метод Адамса
- •Построение метода
- •Метод Милна
- •Построение метода ф ормула прогноза
- •Постановка задачи
- •Варианты заданий
- •Содержание отчёта
- •Вопросы и задания для самоконтроля
Применение интерполяционного полинома Лагранжа для интегрирования
![]() ,
,
где
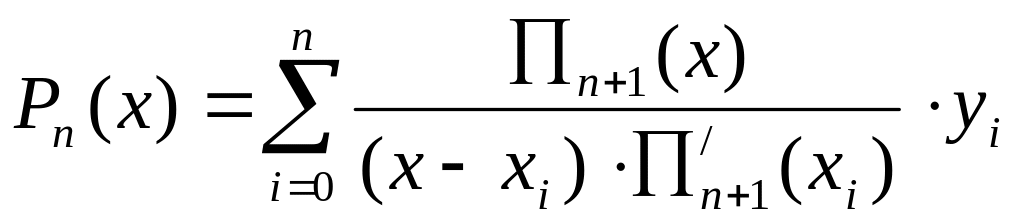 ,
,
![]() погрешность
квадратурной формулы.
погрешность
квадратурной формулы.
Общий вид квадратурной формулы следующий:
![]() ,
где
,
где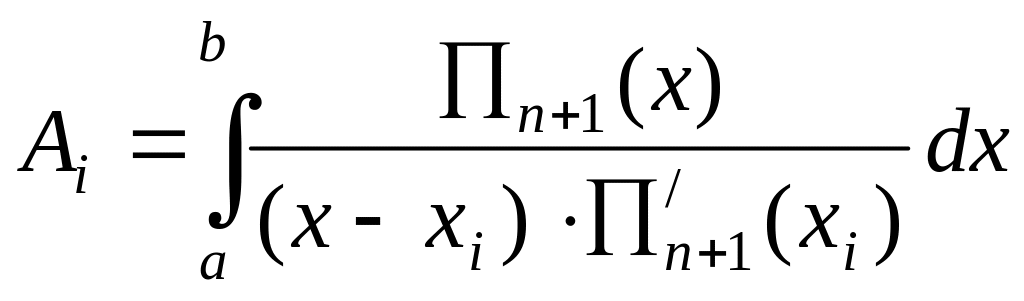 (
).
(
).
Коэффициенты
![]() зависят от выбора узлов.
зависят от выбора узлов.
Замечание.
Если
пределы интегрирования
![]() и
и
![]() являются узлами, то квадратурная формула
называется формулой «замкнутого
типа», в противном случае
«открытого типа».
являются узлами, то квадратурная формула
называется формулой «замкнутого
типа», в противном случае
«открытого типа».
Квадратурные формулы Ньютона–Котеса Пусть , .
Если узлы равноотстоящие
![]() ;
;
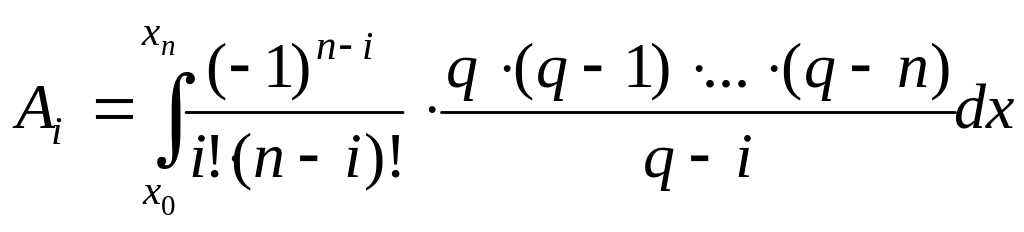 .
.
Так
как
![]() ,
,
![]() ,
то после замены переменной
,
то после замены переменной
![]() (
(![]() ).
).
Так
как
![]() ,
то
,
то
![]() ,
где
,
где
![]()
(![]() коэффициенты
Котеса).
коэффициенты
Котеса).
Квадратурная формула:
![]() (
).
(
).
Замечание.
Коэффициенты
Котеса
![]() обладают свойствами:
обладают свойствами:
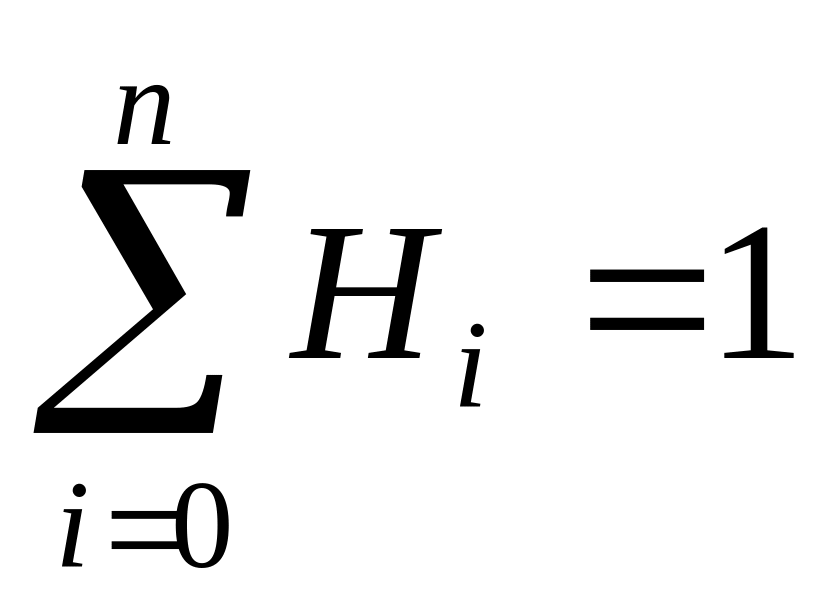 ;
;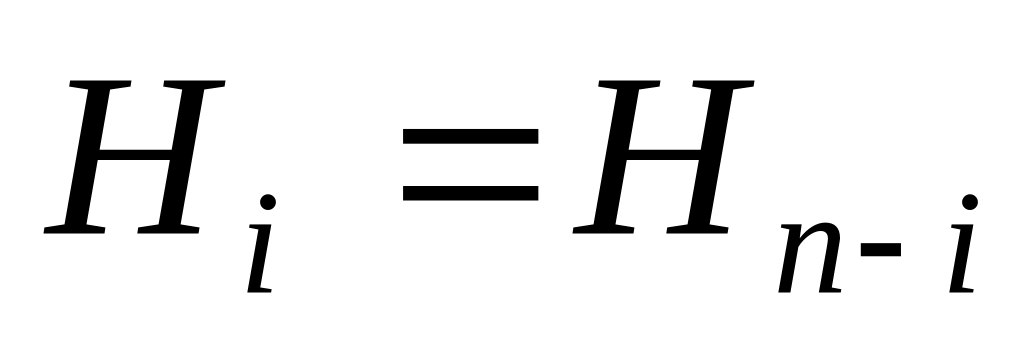 ,
т.е. равноотстоящие от концов интервала
,
т.е. равноотстоящие от концов интервала
 коэффициенты равны.
коэффициенты равны.
Рассмотрим частные случаи.
Формула трапеций (при )
![]() ;
;
![]()
 .
.
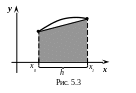
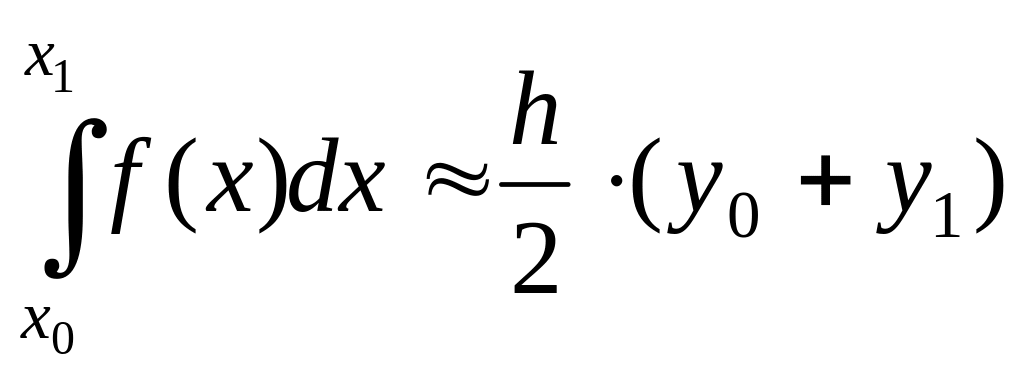 для
частичного интервала (рис. 5.3).
для
частичного интервала (рис. 5.3).
![]()
![]()
![]()
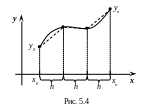 для интервала
(рис. 5.4).
для интервала
(рис. 5.4).
Оценка погрешности квадратурной формулы трапеций
Произведем замену интегрируемой функции интерполяционным полиномом 1-й степени
![]() ,
где
,
где
![]() ;
;
![]() ;
;
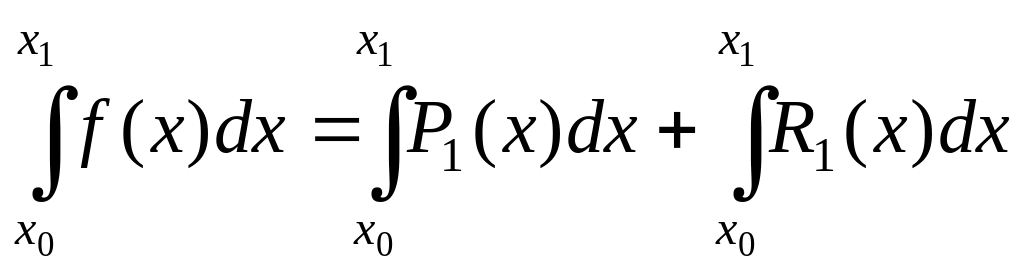 ;
;
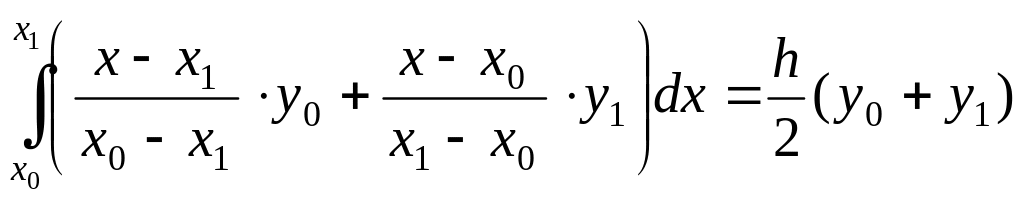 ,
где
,
где
![]() ;
;
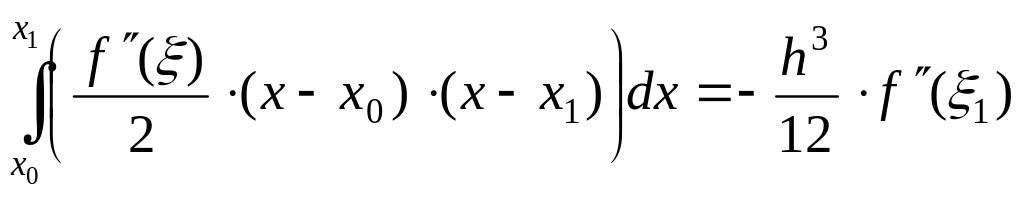 ,
где
,
где
![]() .
.
Полная погрешность
![]() .
.
Полагая
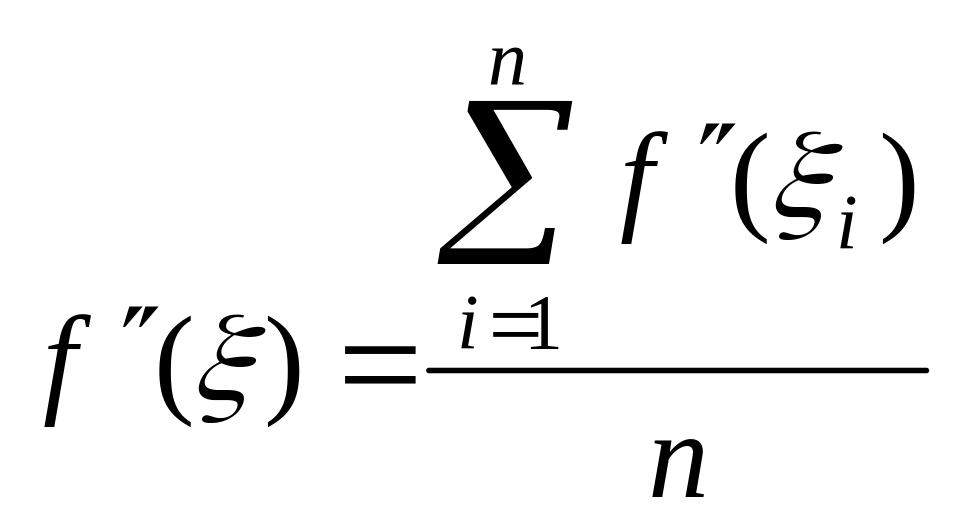
среднее арифметическое
среднее арифметическое
и
учитывая
![]() ,
,
![]() ,
где
,
где
![]() .
.
Выводы:
с ростом интервала интегрирования погрешность возрастает:
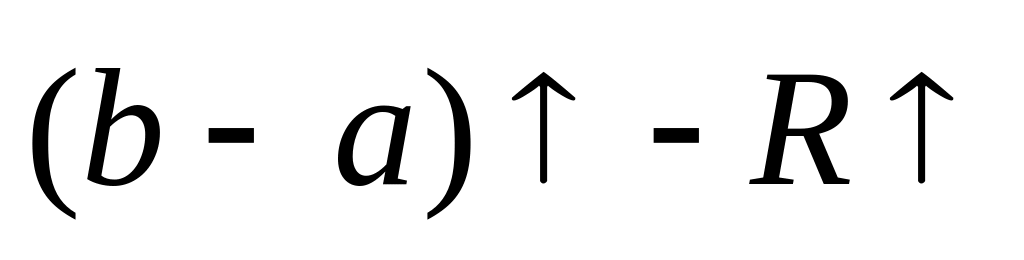 ;
;с ростом количества частичных интервалов погрешность уменьшается:
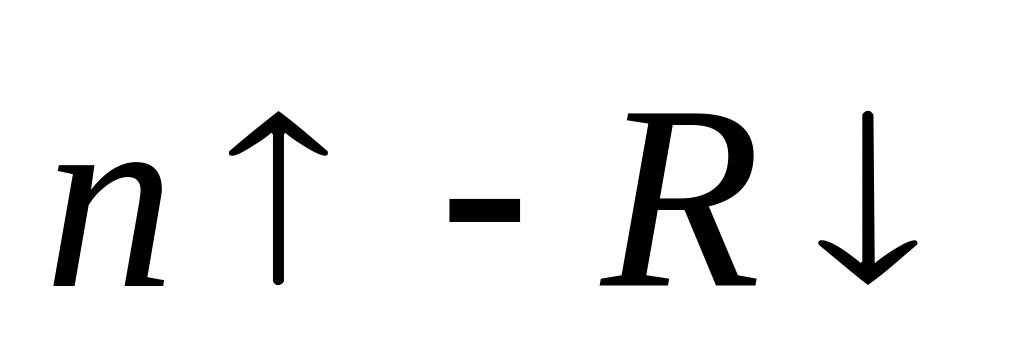 ;
;так как
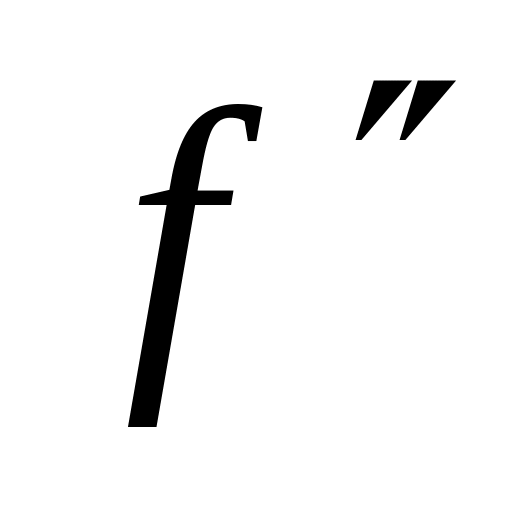 характеризует кривизну функции, то
характеризует кривизну функции, то
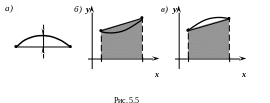
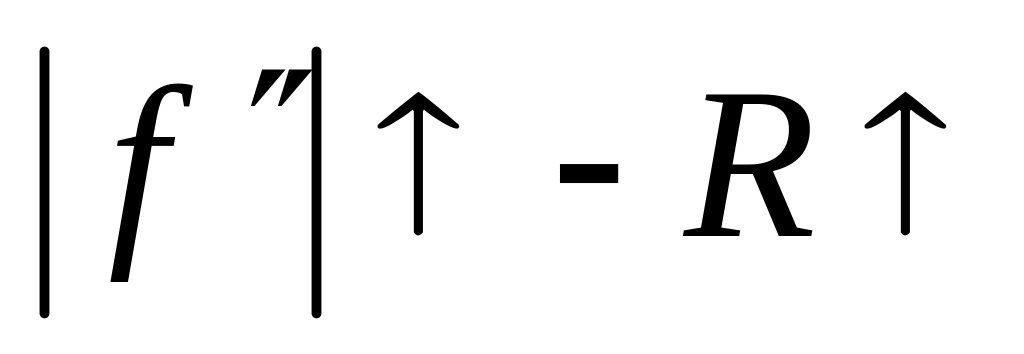 (рис. 5.5, а).
(рис. 5.5, а).
Если
![]() ,
,
![]()
формула дает значение интеграла с
избытком (рис. 5.5, б).
формула дает значение интеграла с
избытком (рис. 5.5, б).
Если
![]() ,
,
![]()
формула дает значение интеграла с
недостатком (рис. 5.5, в).
формула дает значение интеграла с
недостатком (рис. 5.5, в).
Оценка погрешности во многих случаях затруднительна.
Практический способ оценки погрешности (пересчёт с удвоением шага)
![]() ,
где
,
где
![]() const.
const.
![]() ,
где
,
где
![]() –
приближенное значение интеграла,
вычисленное с шагом
.
–
приближенное значение интеграла,
вычисленное с шагом
.
![]() ,
где
,
где
![]() – приближенное
значение интеграла, вычисленное с шагом
– приближенное
значение интеграла, вычисленное с шагом
![]() .
.
Предельная погрешность
![]() .
.
Коррекция результата
![]() .
.
Определение шага
Если
задана предельная допустимая погрешность
![]()
![]() ;
;
![]() .
.
Формула Симпсона (при )
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
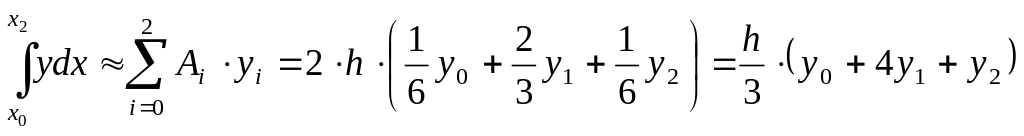 .
.
Г еометрическая
интерпретация квадратурной формулы
(рис. 5.6)
еометрическая
интерпретация квадратурной формулы
(рис. 5.6)
Рис. 5.6
Общая формула Симпсона
![]()
![]() ,
,
где чётное число.
Оценка
погрешности: ![]() .
.
Практическая оценка погрешности
![]() .
.
Замечание.
При одинаковом количестве узлов формула Симпсона по сравнению с формулой трапеций позволяет получить более точный результат.
Квадратурная формула Чебышева
Общий вид квадратурной формулы
![]() .
.
Точность
формулы зависит от выбора: 1) коэффициентов
![]() ;
;
2) узлов .
Вывод формул Ньютона Котеса сводится к подбору коэффициентов при заданных узлах . Вывод формулы Чебышева исходит из иных соображений: определяются узлы при равных коэффициентах.
Переход к стандартному интервалу
Если
![]() ,
,
![]() ,
то
,
то
![]() .
.
После замены переменной
![]() .
.
Квадратурная формула для стандартного интервала:
![]() .
.
Условия, предъявляемые к квадратурной формуле Чебышева:
коэффициенты должны быть одинаковыми
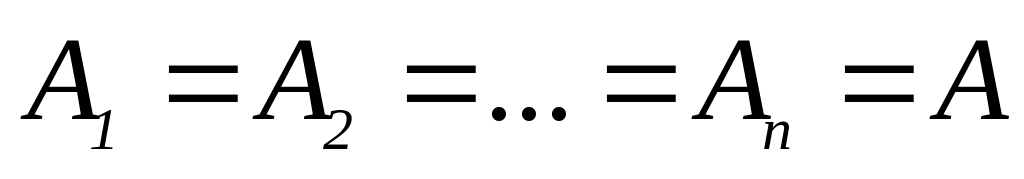 ;
;узлы
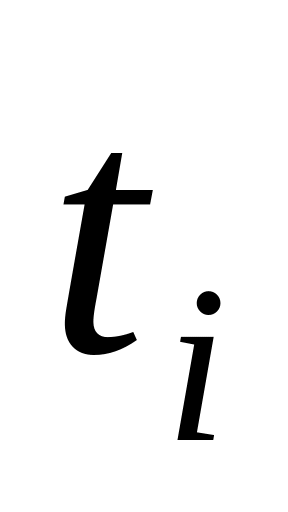 должны выбираться так, чтобы квадратурная
формула была точной для всех полиномов
до максимально возможной степени.
должны выбираться так, чтобы квадратурная
формула была точной для всех полиномов
до максимально возможной степени.
Так
как формула содержит
![]() параметр:
узлов
параметр:
узлов
![]() ,
,
![]() ,…,
,…,
![]() и один коэффициент
и один коэффициент
![]() ,
то максимальная степень полинома равна
.
,
то максимальная степень полинома равна
.
Поиск коэффициента А
Учитывая первое условие
![]() .
.
Полагая
![]() ,
получим:
,
получим:
![]() ,
, ![]() ,
,
![]() .
.
Выбор узлов ti
Согласно
второму условию формула должна быть
точной для функции
![]() вида:
вида:
![]() ,
,
![]() ,…,
,…,![]() .
Подставляя эти функции в квадратурную
формулу, получим систему уравнений:
.
Подставляя эти функции в квадратурную
формулу, получим систему уравнений:
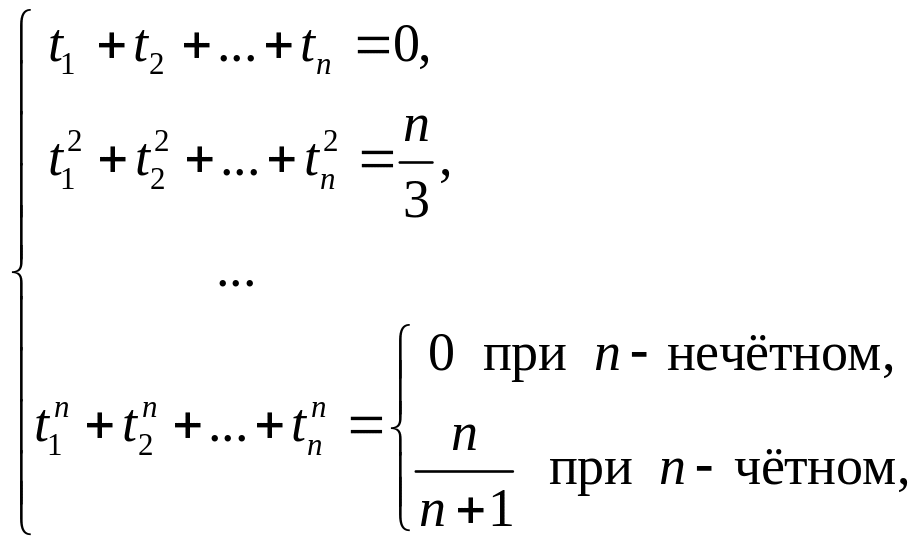
из
которой могут быть определены
(![]() ).
).
Таким образом, квадратурная формула Чебышева имеет вид:
![]() ,
где
,
где
![]()
( см. табл. 5.1).
Таблица 5.1
-
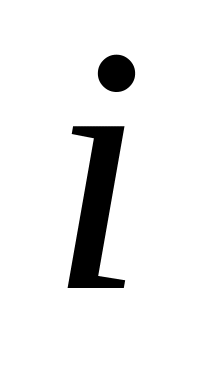
2
1
2
- 0,577 350
0,577 350
1
3
1
2
3
- 0,707 107
0
0,707 107
0,666 667
4
1
2
3
4
- 0,794 654
- 0,187 592
0,187 592
0,794 654
0,5
5
1
2
3
4
5
- 0,832 498
- 0,374 541
0
0,374 541
0,832 498
0,4
6
1
2
3
4
5
6
- 0,866 247
- 0,422 519
- 0,266 635
0,266 635
0,422 519
0,866 247
0,333 333
7
1
2
3
4
5
6
7
- 0,883 862
- 0,529 657
- 0,323 912
0
0,323 912
0,529 657
0,883 862
0,285 714
