§8. Поведение двойных степенных рядов на границе области сходимости.
Рассмотрим обобщение на двойные степенные
ряды второй теоремы Абеля, которая для
простых рядов формулируется следующим
образом: если ряд
сходится, то степенной ряд
сходится абсолютно для всех
и имеет место равенство
.
На двойные степенные ряды теорема Абеля переносится в несколько иной формулировке.
§8.1. Вторая теорема Абеля для ограниченно сходящихся рядов.
Пусть двойной ряд
(22)
ограниченно сходится, т. е. существует
такое число
,
что
где
(23)
Для
и
,
удовлетворяющих неравенствам
рассмотрим двойной степенной ряд
(24)
Теорема 1. Если ряд (22) ограниченно
сходится, то ряд (24) абсолютно сходится
для всех
и
таких, что
,
и имеет место равенство
Доказательство. Т.к.
(25)
то
в силу ограниченной сходимости ряда
(22). Следовательно, для
т. е. ряд (24) абсолютно сходится. В силу (25),
.
Сходимость ряда (22) означает, что для
любого
натуральные
и
такие, что
где
- сумма ряда (22), причем, в силу ограниченной
сходимости этого ряда,
Из очевидного тождества
имеем
откуда
.
Поскольку
,
то для
,
,
,
.
Следовательно,
.
Из этого неравенства следует, что
и фиксированных
и
найдутся числа
такие, что при
и
будем иметь
.
Отсюда следует, что
.
Утверждение теоремы 1 можно обобщить, отказавшись от сходимости ряда (22) и ограничившись сходимостью некоторых средних от частных сумм этого ряда. Пусть
(26)
т. е.
- средние арифметические частных сумм
ряда (22). Справедлива следующая
Теорема 2. Если последовательность
ограничена числом
и существует предел
,
то
.
Доказательство. Из (26) имеем (см. (25)):
,
.
Из этих неравенств следует, что ряды
,
,
сходятся абсолютно для всех
.
Но тогда в силу равенства
(27)
имеем, применяя это равенство еще раз к ряду в правой части и учитывая (26)
(28)
Из (27) и (28) найдем
.
Из существования предела следует, что
(29)
а из условия ограниченности
получим. Что
и, значит,
.
В силу очевидного тождества
имеем
,
где
.
Суммы, стоящие в правой части этого равенства, оцениваются следующим образом
,
,
,
.
Теперь получим оценку
Если
при фиксированных
и
положить
,
,
,
,
то
Следовательно,
.
Замечание. Рассмотрим величины:
,
,
… ,
.
Если существует число
такое, что
,
то последовательно получаются неравенства
;
,
…
,
,
из которых следует абсолютная сходимость
для
,
рядов
,
,
по теореме сравнения. Действительно ,
,
А каждый из полученных справа степенных рядов сходится: первый при , второй – при , т. к. их радиус сходимости
Докажем теперь следующие обобщения теоремы 2.
Теорема 3. Если существует
постоянная
такая, что
и выполняется соотношение
,
то
Доказательство. Пусть
полином
имеет
вид
(члены
низшей степени)
и пусть равенство
(30)
имеет место для всех натуральных
и
.
Покажем, что в этом случае выполняется
равенство
Из очевидного равенства
(31)
найдем:
.
(32)
Это делается следующим образом. Умножая
равенство (31) на
и суммируя по
от 0 до
,
получим:
Далее, производя сдвижку индексов в последних трех суммах, получим:
На основании тождеств
,
,
,
подставляя вместо
,
,
их значения в выражения для
,
получим требуемое равенство (32).
Очевидно, что
(члены
низшей степени)]=
;
;
,
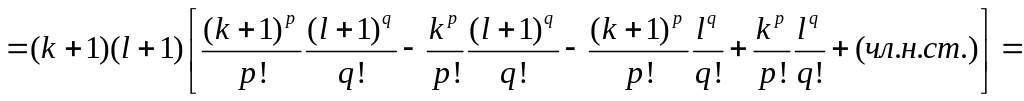
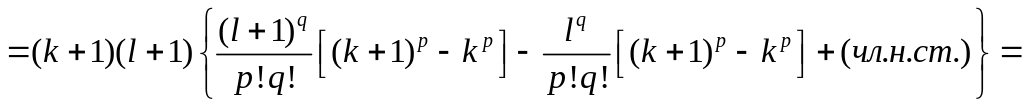
где
,
- полиномы относительно
и
более низших степеней.
В силу условия (30) имеем
;
;
;
.
Из этих равенств и формулы (32) следует, что
.
Теперь предположим, что
и покажем, что выполняется равенство
(30).
Рассмотрим полином
(члены
низшей степени).
Очевидно, что
,
,
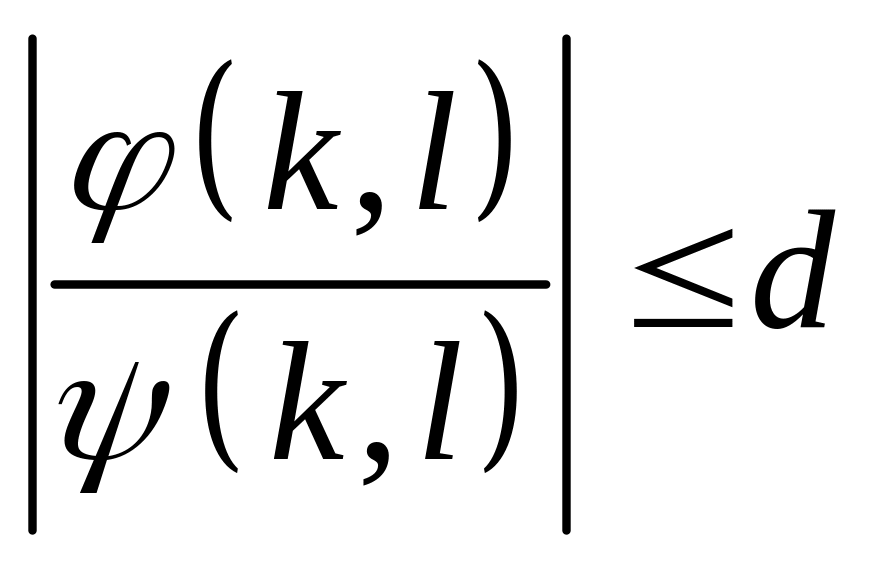где
-
фиксированное число.
Для любого сколь угодно малого наперед заданного найдутся натуральные и такие, что неравенство
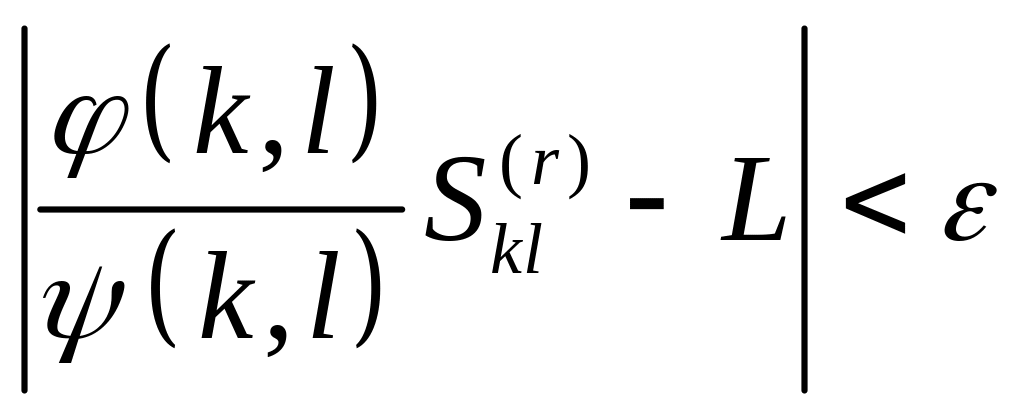
будет выполнятся для всех
.
Т. к. из условий теоремы имеем
,
из предыдущего неравенства следует,
что
.
Далее,
где
.
Для этих сумм получаются следующие оценки:
;
;
;
;
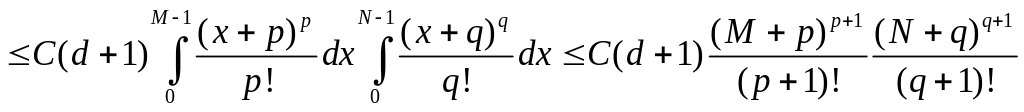С помощью этих оценок найдем
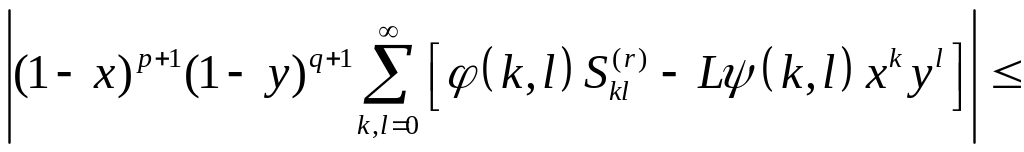
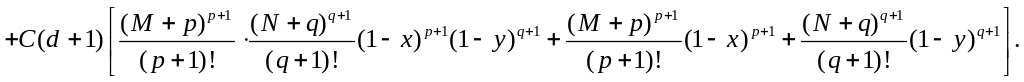
Теперь, при фиксированных
и
можно найти
и
такие, что для всех
будем иметь
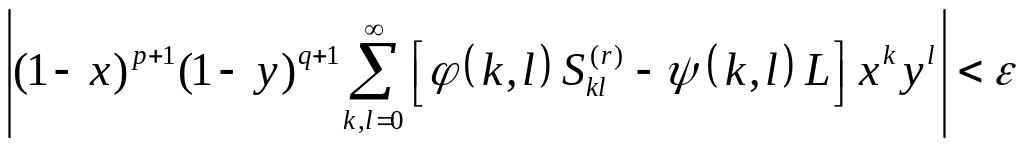
для всех и, следовательно,
.
В силу очевидного (и фактически доказанного выше при нахождении оценок сумм) равенства
из
следует соотношение (30). Поскольку (30)
верно
,
то полагая в (30)
,
получим
,
ч. т. д.