1.Предмет Динамики. Законы механики Галилея-Ньютона. Понятие об инерциальных системах отсчета. Понятие о массе как мере инерции материальной точки.
Динамика- раздел теоретической механики, изучающий движение материальных объектов с учетом сил, вызывающих это движение. В динамике изучаются механические движения материальных объектов под действием сил. Простейшим материальным объектом является материальная точка.
2. Диф. Уравнение движения свобод. Мат. Точ. В декарт.
mx = ∑ Pкx }; my =∑ Pкy }; mz =∑ Pкz }
Естественные уравнения движения мат. точки.
0 = ∑ Pко
md2s/ dt2 = ∑ Pi cos (Pi, τ);
mυ2/ρ = ∑ Pi cos (Pi, n).
3. Две основные задачи динамики. Первая задача динамики.
По заданному движению точки определить силу.
-
уравнения движения точки
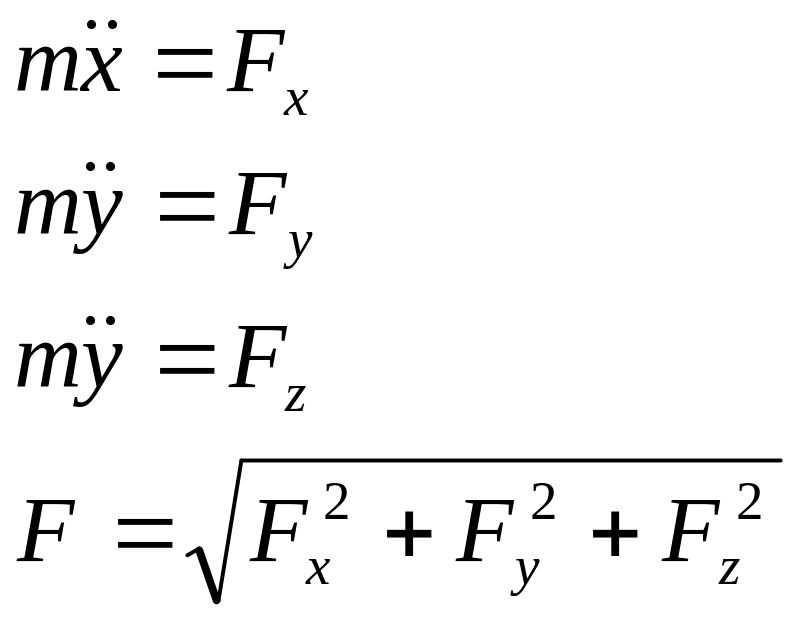
Решается методом дифференцирования.
4. Вторая задача динамики.
Решение второй задачи динамики составляет основное содержание всех разделов динамики.
По заданным силам определить движение точки. Задача решается методом интегрирования.
Если сила зависит только от t или только от x или V, то можно пользоваться следующими указаниями:
1) составить диф.уравнение движения точки:
а) начало координат совмещать с началом движения точки (или с её равновесным положением);
б) если движение по прямой, то одну из осей направить в сторону движения точки;
в) точку изобразить с приложенными силами в произвольном положении;
г) составить диф.уравнение в проекции на ось.
2) интегрирование диф.уравнения.
Замена
переменных.
если
если
Диф.уравнение решать методом разделения переменных(кроме задач на колебания).
3) интегралы брать неопределёнными, учитывая постоянные интегрирования, найденные из начальных условий.
4) анализ движения точки.
8. Диф. Уравнение свободных колебаний мат. Т. И уравнение гармон. Колебательного движения точки.
x + k2x = 0 - Диф. уравнение свободных колебаний мат.
x = A sin(kt+β) - уравнение гармон. колебательного движения точки.
Амплитуда и т.д для свободных колебаний.
A = √x2o + (x0/k)2.
Диф. уравнение затухающих колебаний.
x + 2nx + k2x = 0 - Диф. уравнение.
x = Ae-nt sin (√k2 – n2t + β);
x = Ae-ntsh (√n2 – k2t + β) – апериодическое уравнение.
Период затухающих колебаний, декремент и т.д.
T* = T/√1 – (n/k)2;
e-nT*/2 – декремент, -nT*/2 – логарифмич. декрмент.
n = α/2m – коэф. затухания. k* = √k2 – n2
Диф. уравнение вынужден. кол.
x + k2x = hsin (pt + δ)
Амплитуда и фаза вынуж. кол.
p<k, pt + δ – фаза
AB = h/(k2 – p2)
p>k, pt + δ – π
AB = h/(p2 – k2).
13. Классификация сил, действующих на систему мат. Точек
Силы, действующие на любую точку механической системы, делятся на внутренние и внешние.
Fi – внутренняя сила
Fe – внешняя сила
Внутренними называются силы, с которыми точки, входящие в систему, действуют друг на друга.
Внешними называются силы, которые прикладываются к точкам извне, то есть от других точек или тел, не входящих в систему. Разделение сил на внутренние и внешние условное.
В векторной форме:
,
14. Формулы, определяющие центр масс системы.
xc = ∑mixi/m, yc = ∑m=yi/m, zc = ∑mizi/m
Теорема о движении центра масс мех. системы.
Рассмотрим движущуюся систему мат. точек М1, М2, Мi, Mn, находящихся под действием внешних и внутренних сил (рис). Положение центра масс системы С определяется равенством
rc = ∑miri/m. Уравнения движения точек этой системы имеют вид
mi d2ri/dt2 = PiE + PiJ ; (i = 1, 2, …, n), суммируем эти уравнения:
∑mi d2ri/dt2 =∑ PiE + ∑ PiJ (а). Преобразуем левую часть равенства, учитывая (rc = ∑miri/m) получаем: ∑mi d2ri/dt2 = d2/dt2 * ∑mi ri = d2/dt2 * (mrc) = md2rc/dt2. Геометрическая сумма внутренних сил равна 0. Уравнение (а) приобретает вид: md2rc/dt2 = ∑PiE = RE или
maC = ∑ PiE = RE (в). т.е. произведение массы системы на ускорение её центра масс = геометрической сумме всех действующих на систему внешних сил или главному вектору этих сил. Уравнение (в) выражает теорему о движении центра масс системы, которая формулируется следующим образом: Центр масс мех. сис. движется как мат. точ. массой, равной массе всей системы, к которой приложены все внешние силы действующие на систему.
Проецируя на оси x, y, z – mxC = ∑ XiE = XE