
- •И.А.Гайдукова Математика
- •И.А.Гайдукова Математика
- •Оглавление
- •Введение
- •Рекомендации по выполнению первого задания домашней контрольной работы по теме «Линейная алгебра»
- •1. Элементы теории матриц.
- •2. Линейные операции над матрицами.
- •3. Определитель матрицы
- •4. Обратная матрица
- •Примеры:
- •5. Решение систем линейных уравнений тремя способами.
- •1. Матричный способ решения систем линейных уравнений.
- •2.Решение систем линейных уравнений по формулам Крамера
- •3.Решение систем линейных уравнений методом Гаусса в матричной форме.
- •Рекомендации по выполнению второго задания домашней контрольной работы по теме «Интегральное исчисление» Вычисление интегралов. Замена переменных.
- •Правила интегрирования способом подстановки:
- •Примеры решения интегралов способом подстановки:
- •Рекомендации по выполнению третьего задания домашней контрольной работы по теме «Вычисление площадей плоских фигур и объёмов тел вращения с помощью определённого интеграла»
- •Основные свойства определенного интеграла:
- •Домашняя контрольная работа по математике Варианты заданий. Вариант №1
- •Вариант №8.
- •Вариант №9.
- •Вариант №10.
- •Вариант №15.
- •Список литературы
Правила интегрирования способом подстановки:
Определяют, к какому табличному интегралу приводится данный интеграл (предварительно преобразовав подинтегральное выражение, если нужно).
Определяют, какую часть подинтегральной функции нужно заменить
новой переменной, и записывают эту замену.
Находят дифференциалы обеих частей записи и выражают дифферен-
циал старой переменной (или выражение, содержащее этот диффе-
ренциал) через дифференциал новой переменной.
Производят замену под интегралом.
Находят полученный интеграл.
6. В результате переходят к старой переменной.
Примеры решения интегралов способом подстановки:
Найти : ∫ х²(3+2х
 )
) dx
dx
Решение:
сделаем подстановку 3+2х = t
Найдём дифференциал обеих частей подстановки:
6x![]() dx
= dt,
откуда
dx
= dt,
откуда
х²dx
=
![]() dt.
dt.
Следовательно:
∫ x
(3+2x
)
dx
= ∫ t
∙
![]() dt
=
∫
t
dt
=
∙
dt
=
∫
t
dt
=
∙
![]() +
C
=
+
C
=
![]() t
t![]() +
C
+
C
Заменив t на его выражение из подстановки, получим :
∫ x (3+2x ) dx = (3+2x ) + С
Найти:
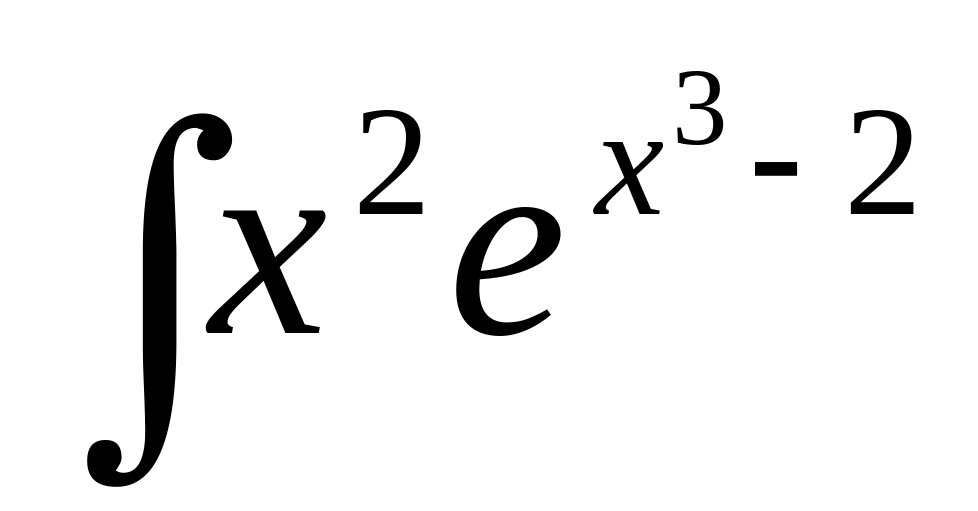
Решение :
=
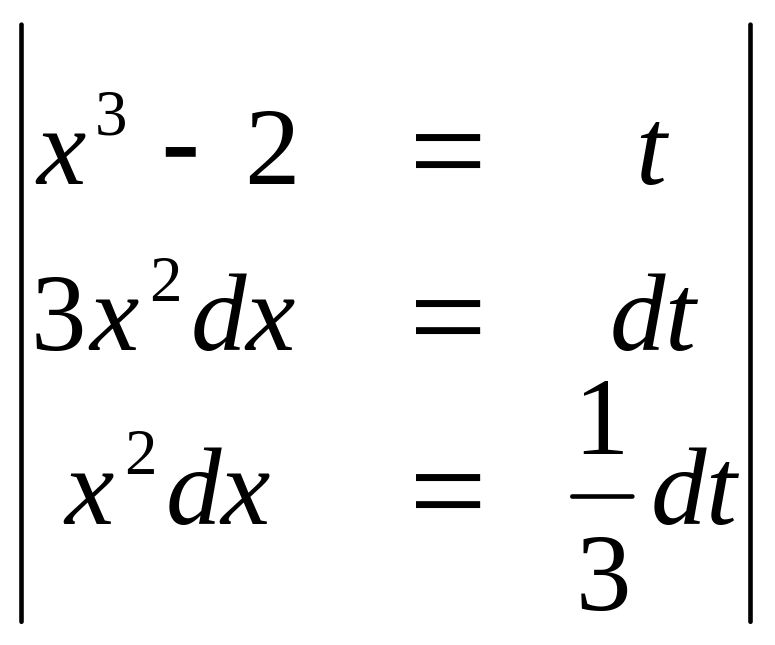 =
=
![]() ∫ е
∫ е![]() =
е
=
е![]() + C =
е
+ C =
е![]() + C
+ C
Найти:
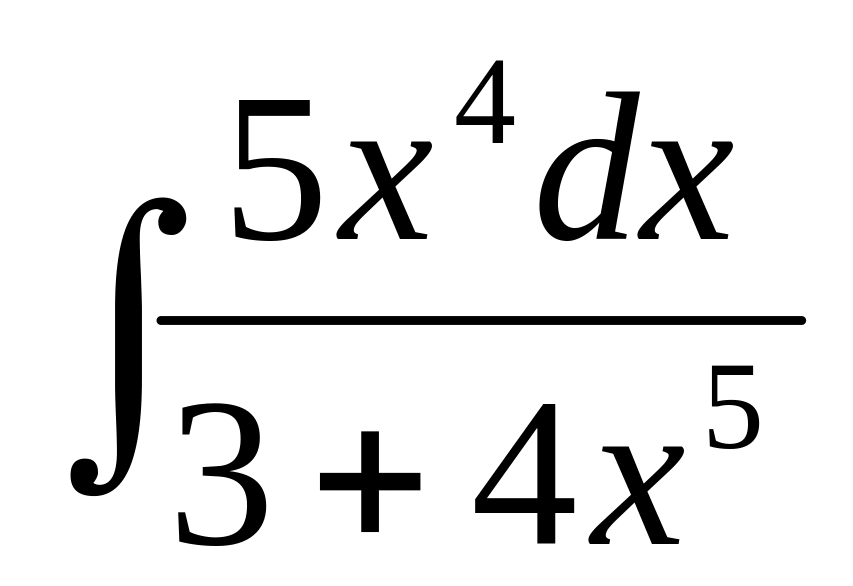
Решение:
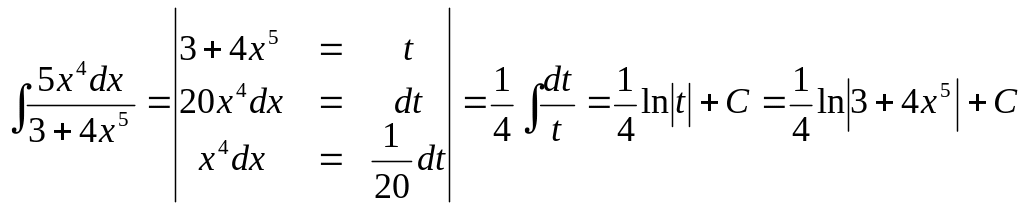
Найти

Решение:
![]()
Найти:
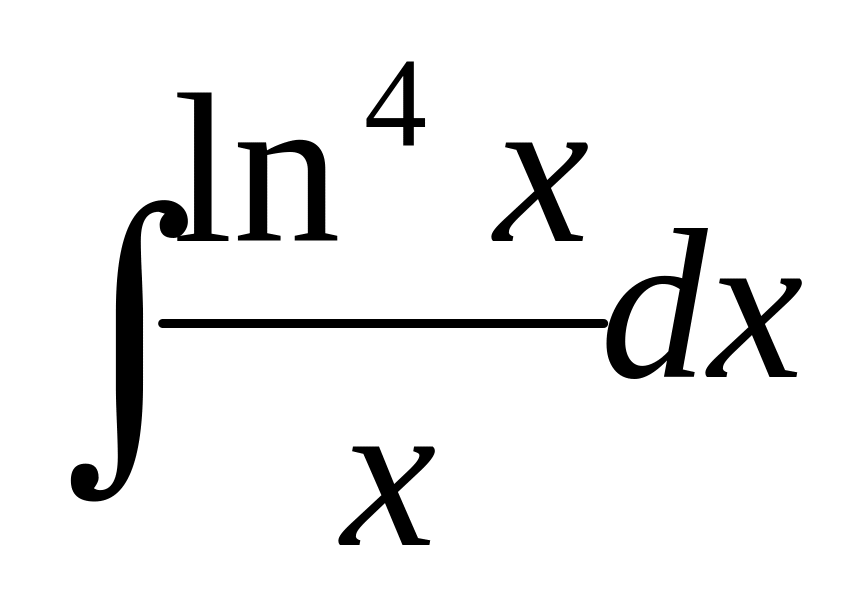
Решение:
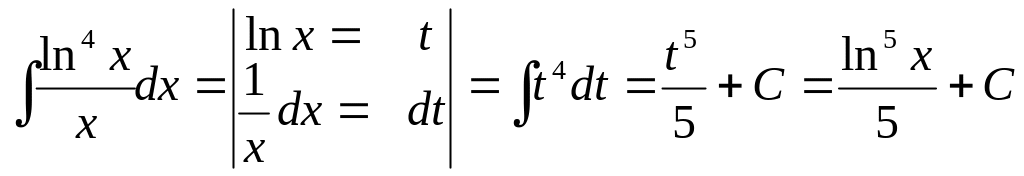
Найти:

Решение:
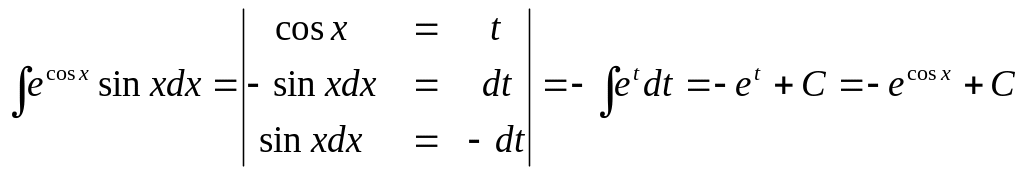
Рекомендации по выполнению третьего задания домашней контрольной работы по теме «Вычисление площадей плоских фигур и объёмов тел вращения с помощью определённого интеграла»
Понятие определённого интеграла.
Разность значений
![]() для любой первообразной функции
для любой первообразной функции
![]() при изменении аргумента от
при изменении аргумента от
![]() до
до
![]() называется определенный интегралом
этой функции в пределах от а до b
и обозначается:
называется определенный интегралом
этой функции в пределах от а до b
и обозначается:
![]()
а и b называются нижним и верхним пределами интегрирования.
Чтобы вычислить определенный интеграл нужно:
Найти соответствующий неопределенный интеграл
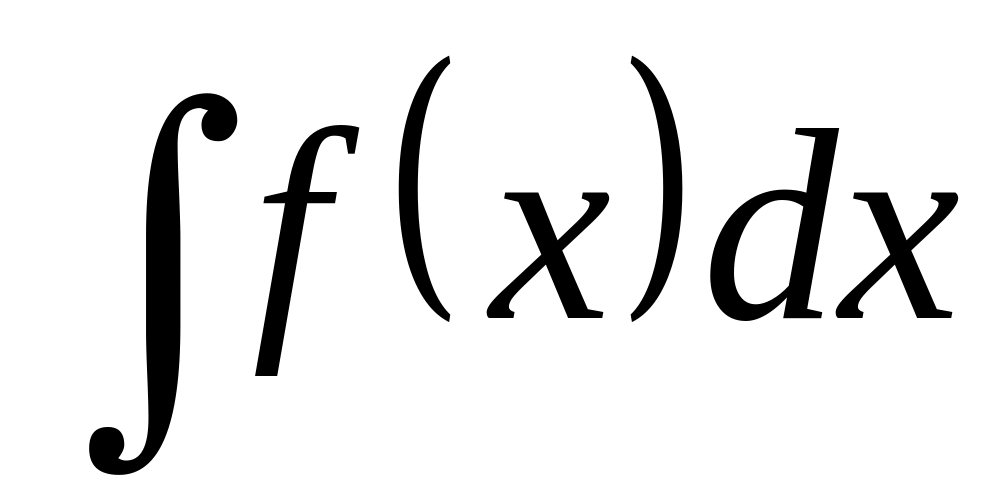
Подставить в полученное выражение вместо х сначала верхний предел интегрирования в, а затем нижний – а.
Из первого результата подстановки вычесть второй.
Коротко это правило записывается в виде формул так:
![]()
Эта формула называется формулой Ньютона - Лейбница.
Основные свойства определенного интеграла:
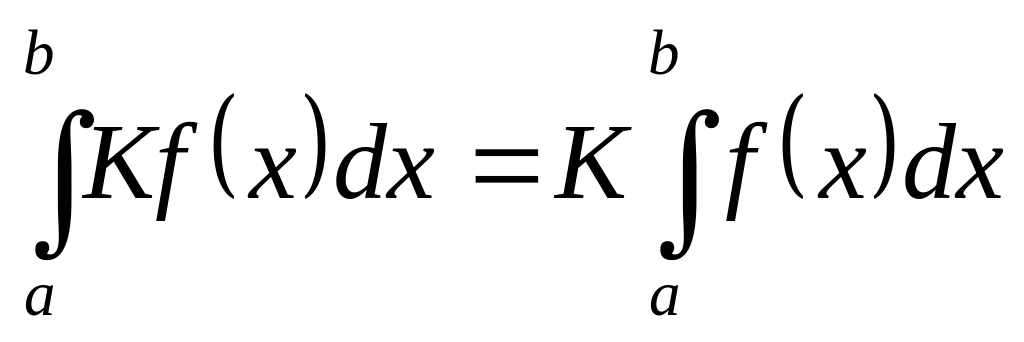 ,
где K=const
,
где K=const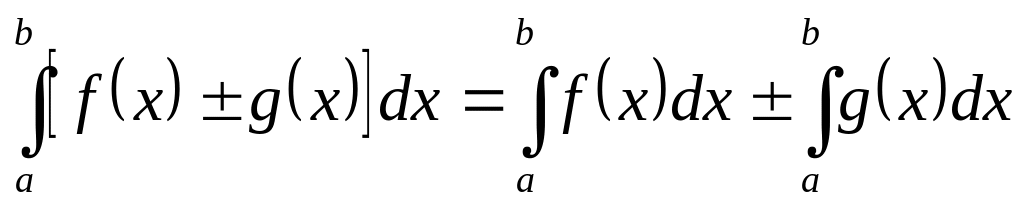
Если
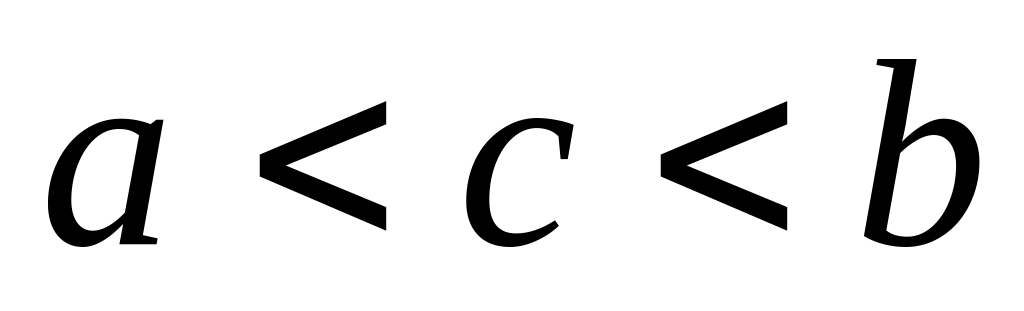 ,
то
,
то
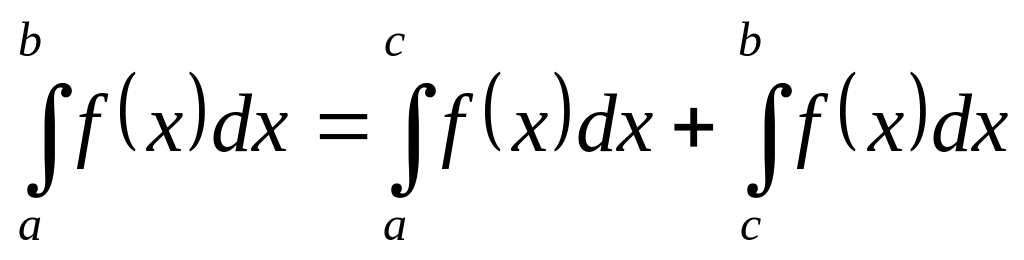
Если функция неотрицательна на отрезке
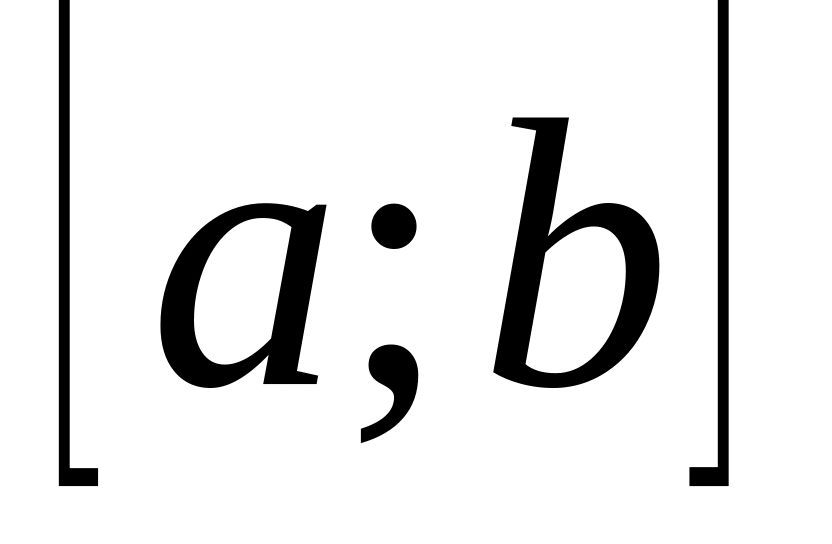 ,
где
,
где
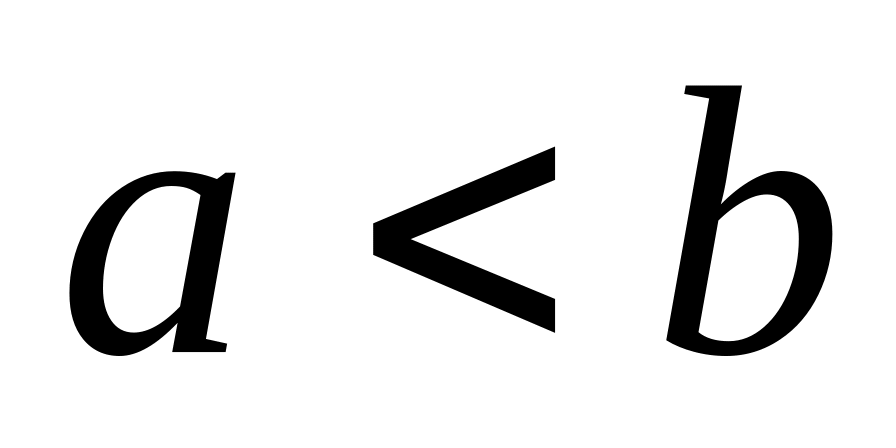 ,
то
,
то
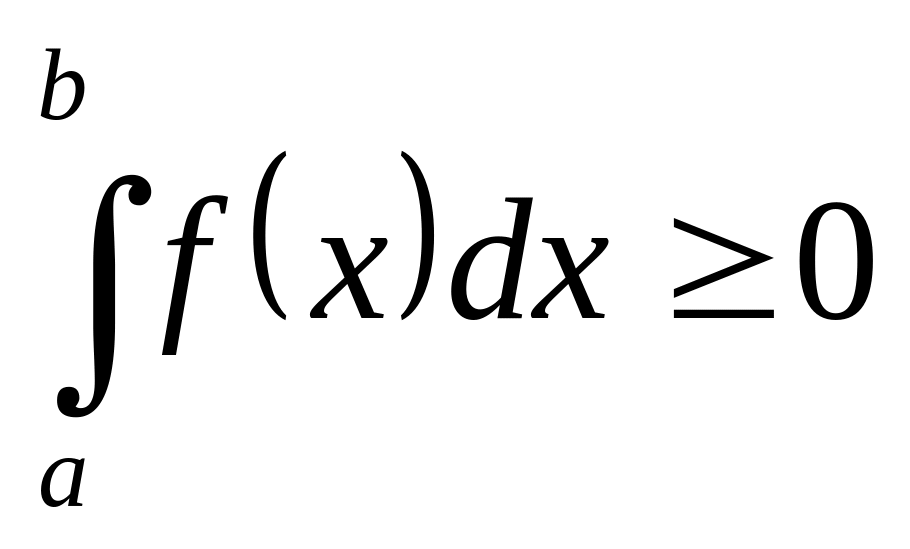
5.
![]()
При замене в определенном интеграле старой переменной интегрирования на новую необходимо старые пределы интегрирования заменить новыми. Эти новые пределы определяются выбранной подстановкой.
Применение определённого интеграла.
Площадь криволинейной
трапеции ограниченной кривой
![]() ,
осью абсцисс и двумя прямыми
и
вычисляется по формуле:
,
осью абсцисс и двумя прямыми
и
вычисляется по формуле:
![]()
Объем тела, образованного вращением вокруг оси абсцисс криволинейной трапеции, ограниченной кривой , не меняющей свой знак на , осью абсцисс и двумя прямыми и вычисляется по формуле:
![]()
С помощью определенного интеграла можно решать и ряд физических задач.
Например:
--Если скорость
прямолинейно движущегося тела
![]() является известной функцией времени
t,
то путь S,
пройденный этим телом с момента времени
t
= t1
до момента
времени t
= t2
определяется формулой:
является известной функцией времени
t,
то путь S,
пройденный этим телом с момента времени
t
= t1
до момента
времени t
= t2
определяется формулой:
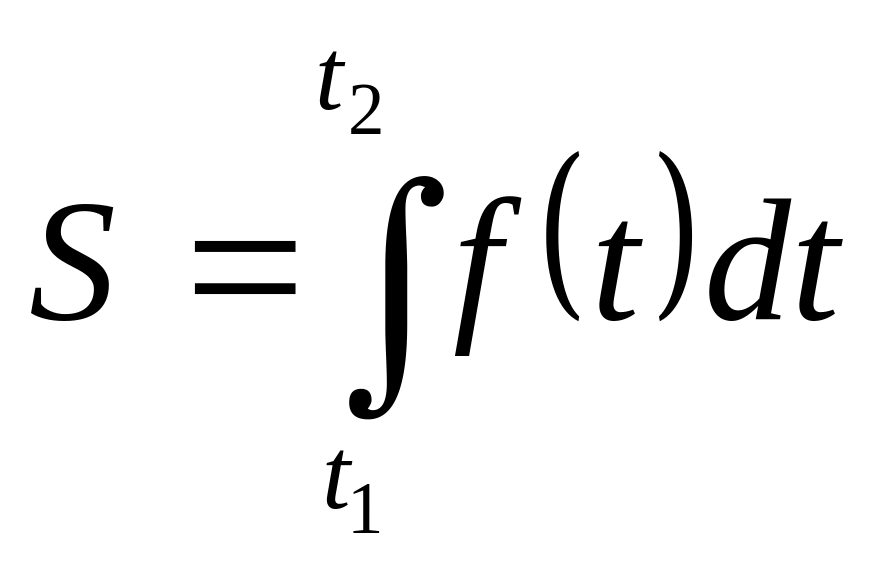
--Если переменная
сила
![]() является известной функцией пути S
(при этом предполагается, что направление
силы не меняется) то работа А, совершаемая
этой силой на пути от
является известной функцией пути S
(при этом предполагается, что направление
силы не меняется) то работа А, совершаемая
этой силой на пути от
![]() до
до
![]() определяется формулой:
определяется формулой:

Примеры:
Вычислить площадь фигуры, ограниченной линиями:
y
=
![]() ;
y
= ( x-2
)2
; 0x.
;
y
= ( x-2
)2
; 0x.
Решение :
а) Построим графики функций: y = ; y = ( x-2 )2
б) Определим фигуру, площадь которой нужно вычислить.
в) Определим пределы интегрирования, решая уравнение: = ( x-2 )2 ; x = 1 ;
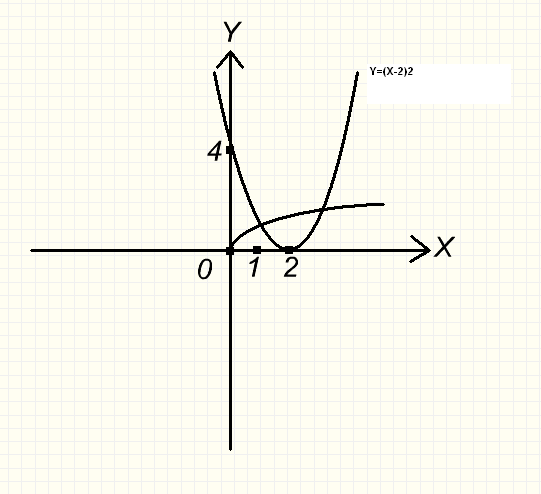
г) Вычисляем площадь заданной фигуры:
S
=
![]() dx
+
dx
+
![]() 2
dx
= 1 ед2
2
dx
= 1 ед2
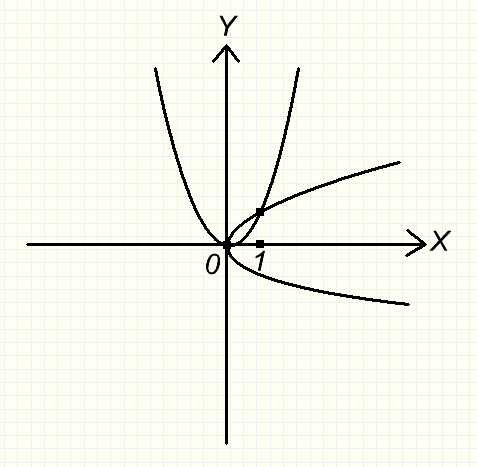
2. Вычислить площадь фигуры, ограниченной линиями :
Y = x2 ; x = y2 .
Решение :
x 2 = ; x 4 = x ;
x ( x 3 – 1 ) = 0
x1 = 0 ; x2 = 1
S
=
![]() - x2)
dx
= (
- x2)
dx
= (
![]() x3\2
-
x3\2
-
![]() )
│01
=
)
│01
=
![]() ед2
ед2
3. Вычислить объём тела , полученного вращением вокруг оси 0x фигуры , ограниченной линиями : y = ; x = 1 .
Решение:
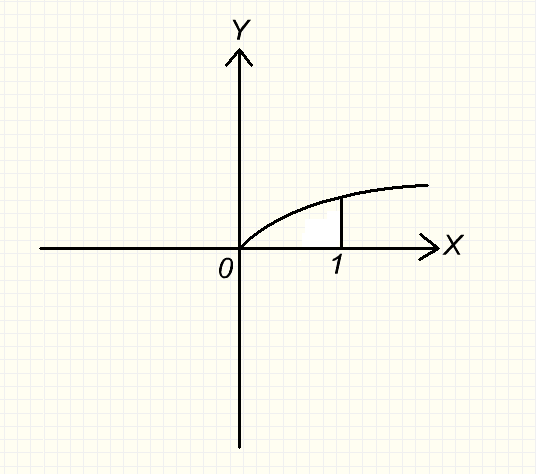
V
= π
![]() dx
= π
)2
dx
=
π
dx
= π
)2
dx
=
π
![]() = π
= π
![]() │
│![]() = π/2
ед.3
= π/2
ед.3
