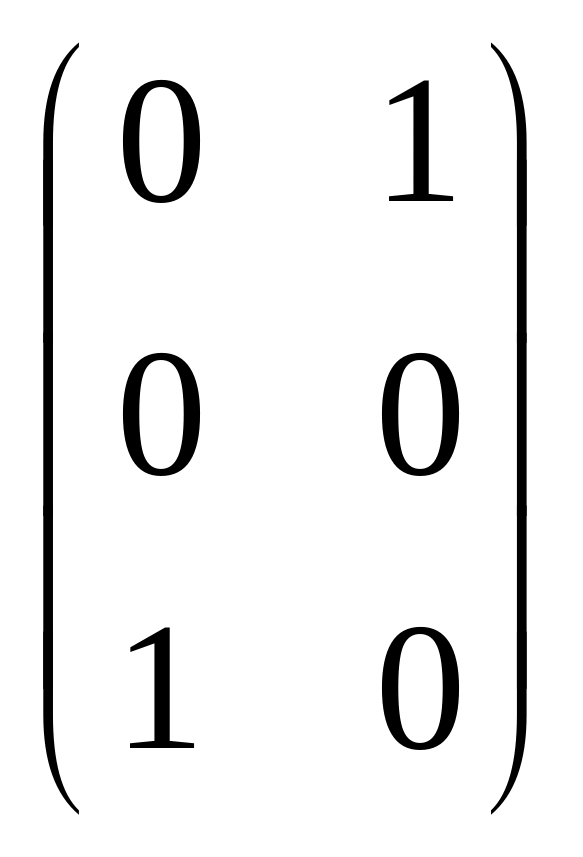
и называется
производной по направлению вектора
.
Если
где
,
то
и эта матрица называется якобианом и обозначается
.
Вторая производная скалярной функции векторного аргумента равна
.
Производная
скалярного произведения по векторному
аргументу:
,
,
.
Производная квадратичной формы по векторному аргументу
.
Производная линейной формы по векторному аргументу
Правила дифференцирования по времени
(следует из
и
)
Если
и
где
x,y
– векторы, то для них определим операции:
,
.
Аналогично можно
записать подобные операции для векторных
функций:
и
где x,y,z
– вектор функции:
.
Разложение в ряд
Тейлора скалярной функции от векторного
аргумента х относительно
точки
,
где R – слагаемые более высокого порядка.
След матрицы.
След квадратной матрицы А, обозначаемой
символом
,
определяется как сумма элементов этой
матрицы, находящихся на главной диагонали.
При этом:
Если
то
.
Символы tr – это сокращение от слова «trace» (след - англ.), часто используют сокращение SpA от немецкого «Spur» – след.
Приведение
матрицы к диагональному виду. Если
для задачи отыскания собственных
значений матрицы
найти
все собственные векторы
матрицы
,
соответствующие собственным значениям
,
т.е.
,
то
можно составить матрицу
из векторов
,
где
.
Тогда справедливо
.
Можно показать, что
.
Это соотношение
является искомым преобразованием,
которое приводит матрицу
к диагональному виду. Это означает, что
если
,
и
,
то
,
.
Приложение 3 п3. Варианты заданий для самостоятельной работы
Задача 1.
Определить, существует ли кривая
,
доставляющая функционалу экстремум и
если существует, то найти её.
Задача 2. Найти,
используя уравнения Эйлера-Лагранжа,
оптимальное управление
,
минимизирующее функционал
для системы, описываемой уравнением
и при фиксированных начальных и конечных условиях соответственно:
В задачах А и В – матрицы,
,
где a>0 – скаляр, а b – скаляр или матрица, в зависимости от размерности u.
№ |
A |
B |
|
|
|
|
a |
b |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 |
|
|
0 |
1 |
|
|
0 |
1 |
2 |
|
|
0 |
1 |
|
|
0 |
1 |
3 |
|
|
0 |
1 |
|
|
0 |
|
4 |
|
|
1 |
3 |
|
|
0 |
1 |
5 |
|
|
1 |
2 |
|
|
1 |
1 |
6 |
|
|
0 |
2 |
|
|
1 |
1 |
7 |
|
|
0 |
1 |
|
|
0 |
1 |
8 |
|
|
1 |
2 |
|
|
0 |
1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
9 |
|
|
1 |
2 |
|
|
0 |
|
10 |
|
|
1 |
2 |
|
|
0 |
1 |
11 |
|
|
0 |
1 |
|
|
0 |
1 |
12 |
|
|
0 |
2 |
|
|
0 |
1 |
13 |
|
|
1 |
3 |
|
|
0 |
1 |
14 |
|
|
0 |
4 |
|
|
0 |
1 |
15 |
|
|
2 |
4 |
|
|
0 |
1 |
16 |
|
|
0 |
2 |
|
|
0 |
|
17 |
|
|
0 |
2 |
|
|
0 |
1 |
18 |
|
|
0 |
1 |
|
|
0 |
1 |
19 |
|
|
0 |
1 |
|
|
0 |
1 |
20 |
|
|
0 |
1 |
|
|
0 |
1 |
21 |
|
|
0 |
1 |
|
|
0 |
1 |
22 |
|
|
0 |
1 |
|
|
0 |
1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
23 |
-1 |
1 |
0 |
2 |
1 |
2 |
1 |
1 |
24 |
1 |
1 |
0 |
1 |
3 |
0 |
1 |
1 |
25 |
2 |
1 |
0 |
2 |
4 |
1 |
1 |
1 |
26 |
-2 |
1 |
0 |
3 |
1 |
4 |
1 |
1 |
27 |
-1 |
1 |
0 |
1 |
2 |
4 |
3 |
1 |
28 |
1 |
1 |
0 |
2 |
6 |
1 |
1 |
4 |
Задача 3. Для системы, описываемой уравнением
с
условиями на начальные
и конечные
значения фазовых координат, найти
оптимальное управление, минимизирующее
функционал
где
функция
и константы a и b
заданы в условии (a – в
общем случае матрица n*n).
№ |
A |
B |
|
|
|
|
|
a |
b |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
1 |
|
|
0 |
1 |
|
|
0 |
0 |
1 |
2 |
|
|
0 |
2 |
|
|
0 |
|
1 |
3 |
|
|
0 |
1 |
|
|
0 |
|
1 |
4 |
|
|
0 |
- |
|
|
0 |
0 |
1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
5 |
|
|
0 |
- |
|
|
0 |
0 |
1 |
6 |
|
|
0 |
1 |
|
|
0 |
|
1 |
7 |
|
|
0 |
1 |
|
|
0 |
|
1 |
8 |
|
|
0 |
1 |
|
|
0 |
|
1 |
9 |
|
|
0 |
2 |
|
|
0 |
|
1 |
10 |
|
|
1 |
2 |
|
|
0 |
|
1 |
11 |
|
|
0 |
1 |
|
|
0 |
|
1 |
12 |
-1 |
1 |
0 |
2 |
1 |
- |
0 |
1 |
1 |
13 |
2 |
1 |
0 |
2 |
2 |
- |
0 |
2 |
1 |
14 |
2 |
1 |
0 |
2 |
2 |
- |
0 |
1 |
2 |
15 |
-1 |
1 |
0 |
2 |
1 |
- |
|
1 |
1 |
16 |
-1 |
1 |
0 |
2 |
1 |
- |
|
0 |
1 |
17 |
0 |
1 |
0 |
2 |
1 |
- |
|
0 |
1 |
18 |
0 |
1 |
0 |
2 |
1 |
- |
|
0 |
1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
19 |
-1 |
1 |
0 |
- |
1 |
- |
|
0 |
1 |
20 |
-1 |
1 |
0 |
- |
1 |
- |
0 |
1 |
1 |
21 |
1 |
1 |
0 |
- |
1 |
- |
0 |
4 |
1 |
22 |
1 |
1 |
0 |
- |
1 |
- |
0 |
1 |
4 |
23 |
-1 |
1 |
0 |
- |
1 |
|
|
1 |
1 |
24 |
-1 |
1 |
0 |
- |
4 |
|
|
4 |
1 |
25 |
-2 |
1 |
0 |
- |
2 |
|
|
1 |
4 |
26 |
-1 |
4 |
0 |
- |
1 |
|
|
1 |
2 |
27 |
-1 |
2 |
0 |
- |
2 |
|
|
2 |
1 |
28 |
-2 |
1 |
1 |
- |
2 |
|
|
1 |
4 |
Задача 4. Используя метод динамического программирования, найти оптимальное управление для системы, описываемой уравнениями
,
Критерий оптимальности имеет вид
№ |
A |
B |
|
|
S |
a |
b |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
1 |
1 |
1 |
0 |
- |
0 |
1 |
1 |
2 |
4 |
1 |
0 |
- |
0 |
4 |
1 |
3 |
2 |
1 |
0 |
- |
0 |
1 |
4 |
4 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
5 |
0 |
1 |
0 |
1 |
2 |
0 |
1 |
6 |
0 |
1 |
0 |
1 |
1 |
0 |
4 |
7 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
8 |
0 |
1 |
0 |
- |
0 |
4 |
1 |
9 |
0 |
1 |
0 |
- |
0 |
1 |
4 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
10 |
1 |
1 |
0 |
- |
0 |
1 |
1 |
11 |
|
|
0 |
- |
0 |
|
1 |
12 |
|
|
0 |
- |
0 |
|
1 |
13 |
|
|
0 |
- |
0 |
|
1 |
14 |
|
|
0 |
- |
0 |
|
1 |
15 |
|
|
0 |
- |
0 |
|
4 |
16 |
|
|
0 |
- |
0 |
|
1 |
17 |
|
|
0 |
- |
0 |
|
1 |
18 |
|
|
0 |
- |
0 |
|
1 |
19 |
|
|
0 |
- |
0 |
|
4 |
20 |
|
|
0 |
- |
0 |
|
1 |
21 |
|
|
0 |
- |
0 |
|
1 |
22 |
|
|
0 |
- |
0 |
|
1 |
23 |
|
|
0 |
- |
0 |
|
4 |
24 |
|
|
0 |
- |
0 |
|
1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
25 |
|
|
0 |
- |
0 |
|
1 |
26 |
|
|
0 |
- |
0 |
|
1 |
27 |
|
|
0 |
- |
0 |
|
1 |
28 |
|
|
0 |
- |
0 |
|
4 |
Задача 5. Используя принцип максимума Понтрягина, решить для линейной системы следующие задачи оптимального управления.
№ |
A |
B |
|
|
|
|
|u| |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
1 |
|
|
0 |
2 |
|
|
|
2 |
|
|
0 |
4 |
|
|
|
3 |
|
|
0 |
3 |
|
|
|
4 |
|
|
0 |
2 |
|
|
|
5 |
|
|
0 |
2 |
|
|
|
6 |
|
|
0 |
4 |
|
|
|
7 |
|
|
0 |
3 |
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
8 |
|
|
0 |
4 |
|
|
|
9 |
|
|
0 |
4 |
|
|
|
10 |
|
|
0 |
2 |
|
|
|
11 |
|
|
0 |
1 |
|
|
|
12 |
|
|
0 |
2 |
|
|
|
13 |
|
|
0 |
1 |
|
|
|
14 |
|
|
0 |
3 |
|
|
|
15 |
|
|
0 |
2 |
|
|
|
16 |
|
|
0 |
1 |
|
|
|
17 |
|
|
0 |
|
|
|
|
18 |
|
|
0 |
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
19 |
|
|
0 |
|
|
|
|
20 |
|
|
0 |
|
|
|
|
21 |
|
|
0 |
|
|
|
|
22 |
|
|
0 |
|
|
|
|
23 |
|
|
0 |
|
|
|
|
24 |
|
|
0 |
|
|
|
|
25 |
|
|
0 |
|
|
|
|
26 |
|
|
0 |
|
|
|
|
27 |
|
|
0 |
|
|
|
|
28 |
|
|
0 |
|
|
|
|
Задача 6. Установить управляемость и наблюдаемость линейных систем, описываемых уравнениями:
Если система не вполне управляема, то оценить её стабилизируемость, а если не вполне наблюдаема – обнаруживаемость.
№ |
A |
B |
C |
1 |
2 |
3 |
4 |
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
1 |
2 |
3 |
4 |
11 |
|
|
|
12 |
|
|
|
13 |
|
|
|
14 |
|
|
|
15 |
|
|
|
16 |
|
|
|
17 |
|
|
|
18 |
|
|
|
19 |
|
|
|
20 |
|
|
|
1 |
2 |
3 |
4 |
21 |
|
|
|
22 |
|
|
|
23 |
|
|
|
24 |
|
|
|
25 |
|
|
|
26 |
|
|
|
27 |
|
|
|
28 |
|
|
|
Задача 7. Для линейных систем выполнить синтез оптимального управления для квадратичного критерия
или установить невозможность синтеза и указать причину.
№ |
A |
B |
Q |
R |
1 |
2 |
3 |
4 |
5 |
1 |
|
|
|
1 |
2 |
|
|
|
1 |
3 |
|
|
|
1 |
4 |
|
|
|
4 |
5 |
|
|
|
1 |
6 |
|
|
|
1 |
7 |
|
|
|
2 |
8 |
|
|
|
1 |
9 |
|
|
|
4 |
10 |
|
|
|
1 |
11 |
|
|
|
4 |
12 |
|
|
|
4 |
13 |
|
|
|
4 |
14 |
|
|
|
1 |
1 |
2 |
3 |
4 |
5 |
15 |
|
|
|
1 |
16 |
|
|
|
1 |
17 |
|
|
|
1 |
18 |
|
|
|
1 |
19 |
|
|
|
1 |
20 |
|
|
|
4 |
21 |
|
|
|
1 |
22 |
|
|
|
2 |
23 |
|
|
|
1 |
24 |
|
|
|
4 |
25 |
|
|
|
1 |
26 |
|
|
|
2 |
27 |
|
|
|
1 |
28 |
|
|
|
1 |
Примечание:
Если в условии для фазовых координат
или
указан символ
,
то это указывает, что данный параметр
свободен.