Сравнение бесконечно малых величин

Зададимся вопросом, как можно сравнить две бесконечно малые величины или две бесконечно большие величины?

Определения. Пусть при   функции f(x) и g(x) являются бесконечно малыми. Тогда:

2. Если   , то f(x) называется бесконечно малой высшего порядка относительно g(x).

2. Если   (конечен и отличен от 0), то f(x) называется бесконечно малой n-го порядка относительно g(x).

3. Если   , то f(x) и g(x) называются эквивалентными бесконечно малыми.Эквивалентность записывается так:   .

Свойства эквивалентных бесконечно малых:

1. Разность двух эквивалентных бесконечно малых есть бесконечно малая высшего порядка относительно каждой из них.

2. Если из суммы нескольких бесконечно малых разных порядков отбросить бесконечно малые высших порядков, то оставшаяся часть, называемая главной, эквивалентна всей сумме.

Из первого свойства следует, что эквивалентные бесконечно малые могут сделаться приближенно равными со сколь угодно малой относительной погрешностью. Поэтому знак  мы применяем как для обозначения эквивалентности бесконечно малых, так и для записи приближенного равенства их достаточно малых значений. 

Билет 11

А)Эллипс

Эллипсом называется геометрическое место точек, для которых сумма расстояний до двух фиксированных точек (фокусов) есть для всех точек эллипса одна и та же постоянная величина (эта постоянная величина должна быть больше, чем расстояние между фокусами).

Простейшее уравнение эллипса

где a - большая полуось эллипса, b - малая полуось эллипса. Если 2c - расстояние между фокусами, то между a, b и c (если a > b) существует соотношение

Б)Непрерывность функции. Связь между непрерывность и дифференцируемостью

Непрерывность функции

Определение. Функция   называется непрерывной в точке   , если она определена в некоторой окрестности точки   и выполняется равенство:

Данное определение эквивалентно следующим четырем условиям непрерывности:

1. Функция   должна быть определена в некоторой окрестности точки   ;

2. Должны существовать конечные односторонние пределы

   и

3. Эти односторонние (левый и правый) пределы должны совпадать:

4. Эти пределы должны быть равны   :

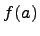Определение. Функция   называется непрерывной на отрезке   , если она непрерывна в каждой точке внутри отрезка, а на его концах выполняются равенства:

   и

Связь между дифференцируемостью и непрерывностью функции

Рассмотрим следующие вопросы, который касаются функций.

Если функция непрерывна, то она дифференцируема?

Если функция дифференцируема, то она непрерывна?

Ответ на первый вопрос: из непрерывности функции не следует ее дифференцируемость.

Ответ на второй вопрос: из дифференцируемости функции следует ее непрерывность.

Рассмотрим более конкретно каждый вопрос. Чтобы ответить на данные вопросы необходимо доказать озвученый факт или привести пример, который опровергает этот факт.

Найдем производную следующей функции   . Хорошо известно, данная функция является непрерывной и, что ее производная будет следующей:

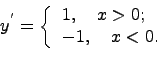
Покажем, что в точке нуль производная не существут. Для этого найдем производную в нуле по определению производной:

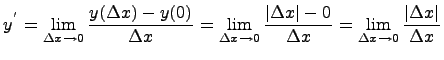
данный предел равен 1, если   и равен (-1), если   , получаем, что предел не существует, следовательно в нуле производной нет и функция в нуле не дифференцируема. 

Билет 12

А)Гипербола

Гиперболой называется геометрическое место точек, разность расстояний которых от двух данных фиксированных точек (фокусов) гиперболы есть одна и та же постоянная величина. Предполагается, что эта постоянная величина не равна нулю и меньше, чем расстояние между фокусами.

Простейшее уравнение гиперболы

Б)Исследование функции на возрастание, убывание. Экстремумы

Определение. Функция   называется возрастающей в точке   , если в некоторой   -окрестности этой точки справедливо

для любого   .

Определение. Функция   называется возрастающей на отрезке   , если для любых двух точек   справедливо неравенство

когда   .

Определение. Функция   называется убывающей в точке   , если в некоторой   -окрестности этой точки справедливо неравенство

для любого   .

Определение. Функция   называется убывающей на отрезке   , если для любых двух точек   справедливо неравенство

когда   .

Определение. Функция   имеет в точке   максимум, если значение   является наибольшим в некоторой двустороней окрестности точки   .

Определение. Функция   имеет в точке   минимум, если значение   является наименьшим в некоторой двусторонней окрестности точки   .

Определение. Функция   имеет в точке   экстремум, если точка   является точкоймаксимума или минимума.

Признаки (достаточные) возрастания и убывания функции   :

Если   на интервале   , то функция   возрастает на этом интервале;

Если   на интервале   , то функция   убывает на этом интервале.

Необходимое условие экстремума функции.

Функция   может иметь экстремум только в точках, где   или производная не существует. Точка, где   или производная не существует называется критической точкой.

Заметим, что если в точке   выполняется, что   , то это означает, что касательная в данной точке параллельная оси   . Если производная в точке   не существует, то это значит либо касательная вертикальная, либо ее нет в данной точке.

Достаточные условие экстремума функции.

Если функция   непрерывна в точке   и имеет в некоторой окрестности точки   , кроме, быть может самой точки   , конечную производную и если при переходе   через точку  :

 меняет знак с '+' на '-', то точка   -- точка максимума;

 меняет знак с '-' на '+', то точка   -- точка минимума;

 не меняет знак, то точка   не является точкой экстремума.

Билет 13

А)Парабола

Параболой называется геометрическое место точек, каждая из которых одинаково удалена от заданной фиксированной точки и от заданной фиксированной прямой. Точка, о которой идет речь в определении, называется фокусом параболы, а прямая - ее директрисой.

Простейшее уравнение параболы

y² = 2px.     (*)

Б)Исследование функции на выпуклость, вогнутость в точке перегиба

Функция  f ( x ) называется  выпуклой  на интервале ( a, b ), если её график на этом интервале лежит  ниже  касательной, проведенной к кривой  y = f (x ) в любой точке ( x₀ ,  f ( x₀ ) ),  x₀   ( a, b ).

Функция  f ( x ) называется  вогнутой на интервале ( a, b ), если её график на этом интервале лежит  выше  касательной, проведенной к кривой  y = f (x ) в любой точке ( x₀ ,  f ( x₀ ) ),  x₀   ( a, b ).

 

Достаточное условие вогнутости ( выпуклости ) функции.

Пусть функция f ( x ) дважды дифференцируема ( имеет вторую производную ) на интервале ( a, b ), тогда:

если  f '' ( x ) > 0 для любого x   ( a, b ), то функция  f ( x ) является вогнутой на интервале ( a, b );

если  f '' ( x ) < 0 для любого x   ( a, b ), то функция  f ( x ) является выпуклой на интервале ( a, b ) .

 

Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкой перегиба. Отсюда следует, что если в точке перегиба  x₀  существует вторая производная  f '' ( x₀ ), то  f '' ( x₀ ) = 0.

Билет 14

А)Действия с матрицамиМатрицей размера n * x называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы.

Операция сложения матриц вводится только для матриц одинакового размера, т. е. дляматриц, у которых число строк и столбцов соответственно равно. Суммой матриц А и В, называется матрица С, элементы которой равны сумме соответствующих элементов.

Аналогично определяется разность матриц.

Умножение матрицы на число:

Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число. Произведением матрицы А на число k называется матрица В, такая что bij = k × aij.

Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы. Произведением матрицы Аm×n на матрицу Вn×p, называется матрица Сm×p такая, что сik = ai1 × b1k + ai2 × b2k + ... + ain × bnk, т. е. находиться сумма произведений элементов i - ой строки матрицы А на соответствующие элементы j - ого столбца матрицы В. Если матрицы А и В квадратные одного размера, то произведения АВ и ВА всегда существуют. Легко показать, что А × Е = Е × А = А, где А квадратная матрица, Е - единичная матрица того же размера

Б)Вертикальные и наклонные(горизонтальные) асимптоты