
- •Критерии однородности дисперсии нескольких независимых выборок.
- •Понятие квантили (определение, графическая интерпретация), доверительного интервала, доверительной области. Примеры нахождения квантилей нормального распределения.
- •Критерии однородности выборок. Критерий Смирнова.
- •Доверительные интервалы для дисперсии нормального распределения.
- •Критерии однородности выборок. Критерий однородности хи-квадрат Пирсона
- •Доверительные интервалы для дисперсии нормального распределения.
- •Критерий проверки значимости линейной регрессии (два подхода).
- •Понятие одномерной и двумерной функции распределения случайного процесса и плотности распределения. Вероятностный смысл.
- •Простые и сложные гипотезы. Статистический критерий различения гипотез. Уровень значимости и мощность критерия. Ошибки первого и второго рода.
- •Числовые характеристики случайных процессов (определение, свойства). Корреляционная теория случайных процессов.
- •Лемма Неймана — Пирсона. Наиболее мощные критерии
- •2. Математическое ожидание суммы случайных величин
- •Наиболее мощные критерии различения двух простых гипотез о среднем значении гауссовской случайной величины при известной дисперсии.
- •Дискретный вариационный ряд. Полигон частот и относительных частот.
- •Наиболее мощные критерии различения двух простых гипотез о среднем значении гауссовской случайной величины при неизвестной дисперсии.
- •Доверительные интервалы для математического ожидания нормального распределения.
- •Лемма Неймана — Пирсона. Наиболее мощные критерии
- •2. Математическое ожидание суммы случайных величин
- •Сравнение дисперсий двух гауссовских выборок. Критерий Фишера.
- •Интервальный вариационный ряд. Гистограмма частот и относительных частот.
- •Сравнение средних двух гауссовских выборок с равными дисперсиями. Критерий Стьюдента.
- •Дискретный вариационный ряд. Полигон частот и относительных частот.
- •1.Сравнение исправленной выборочной дисперсии с гипотетической генеральной дисперсией.
- •2.Сравнение средних двух гауссовских зависимых выборок.
- •Критерий
- •Понятие статистики как функции от выборки
- •Статистика критерия
- •Оценки максимального правдоподобия параметров нормального распределения.
- •Метод наименьших квадратов для случая квадратичной зависимости и обобщенной линейной зависимости данных.
- •1.Оценки подстановки неизвестных параметров. Выборочное среднее и выборочная дисперсия. Несмещенная оценка дисперсии.
- •2.Методы линейной регрессии. Метод наименьших квадратов для случая линейной зависимости данных.
- •1.Критерий согласия хи-квадрат Пирсона различения статистических гипотез (случай распределения с неизвестными параметрами).
- •Статистика критерия
- •1.Вариационный ряд. Распределения порядковых статистик выборки (максимальной и минимальной варианты выборки).
- •2.Эмпирическая функция распределения и её свойства. Пример нахождения эмпирической функции и построение ее графика.
- •1.Усиленный закон больших чисел. Теорема Колмогорова и теорема Бореля.
- •2.Оценки подстановки неизвестных параметров. Выборочное среднее и выборочная дисперсия. Несмещенная оценка дисперсии.
Лемма Неймана — Пирсона. Наиболее мощные критерии
Пусть - выборка (набор независимых, одинаково распределенных величин), и имеются две гипотезы о распределении :
Предполагается, что распределения , либо оба дискретны, либо оба абсолютно непрерывны.
Для любого НМК уровня существует и совпадает с критерием отношения правдоподобия:
при этом и определяются из уравнения , или
(7.1)
Доказательство леммы Неймана - Пирсона
1. Докажем, что уравнение (7.1) разрешимо относительно и .
Рассмотрим невозрастающую функцию .
Поскольку интегрирование ведется по области , то под интегралом . Поэтому
при .
Рассмотрим :
Возможны два критерия: (а) и (б) .
2. Математическое ожидание суммы случайных величин
Докажем, что для любых двух случайных величин и
, (10.2.3)
т. е. математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий.
Это свойство известно под названием теоремы сложения математических ожиданий.
Доказательство.
а) Пусть - система прерывных случайных величин. Применим к сумме случайных величин общую формулу (10.1.6) для математического ожидания функции двух аргументов:
.
Ho представляет собой не что иное, как полную вероятность того, что величина примет значение :
;
следовательно,
.
Аналогично докажем, что
,
и теорема доказана.
б) Пусть - система непрерывных случайных величин. По формуле (10.1.7)
. (10.2.4)
Преобразуем первый из интегралов (10.2.4):
аналогично
,
и теорема доказана.
Следует специально отметить, что теорема сложения математических ожиданий справедлива для любых случайных величин - как зависимых, так и независимых.
Теорема сложения математических ожиданий обобщается на произвольное число слагаемых:
, (10.2.5)
т. е. математическое ожидание суммы нескольких случайных величин равно сумме их математических ожиданий.
Для доказательства достаточно применить метод полной индукции.
Дисциплина: ТВ и МС Билет № 10
Сравнение дисперсий двух гауссовских выборок. Критерий Фишера.
Сравнение математических ожиданий проводят в тех случаях, когда требуется установить соответствие показателей качества изготовленной продукции и эталонного образца. Это — задача проверки гипотезы:
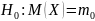
где m0 — значение, соответствующее эталонному образцу; X — случайная величина, моделирующая результаты наблюдений. В зависимости от формулировки вероятностной модели ситуации и альтернативной гипотезы сравнение математических ожиданий проводят либо параметрическими, либо непараметрическими методами.
Сравнение дисперсий проводят тогда, когда требуется установить отличие рассеивания показателя качества от номинального. Для этого проверяют гипотезу:
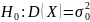
Ряд иных постановок задач одномерной статистики приведён ниже. Не меньшее значение, чем задачи проверки гипотез, имеют задачи оценивания параметров. Они, как и задачи проверки гипотез, в зависимости от используемой вероятностной модели ситуации делятся на параметрические и непараметрические.
В
параметрических задачах оценивания
принимают вероятностную модель, согласно
которой результаты наблюдений  рассматривают
как реализации n независимых
случайных величин с функцией
распределения F(x;θ).
Здесь θ — неизвестный параметр,
лежащий в пространстве параметров Θ заданном
используемой вероятностной моделью.
Задача оценивания состоит в определении
точечной оценок и доверительных границ
(либо доверительной области) для
параметра θ.
рассматривают
как реализации n независимых
случайных величин с функцией
распределения F(x;θ).
Здесь θ — неизвестный параметр,
лежащий в пространстве параметров Θ заданном
используемой вероятностной моделью.
Задача оценивания состоит в определении
точечной оценок и доверительных границ
(либо доверительной области) для
параметра θ.
Параметр θ — либо число, либо вектор фиксированной конечной размерности. Так, для нормального распределения θ = (m,σ2) — двумерный вектор, для биномиального θ = p — число, для гамма-распределения θ = (a,b,c) — трёхмерный вектор, и так далее.
В современной математической статистике разработан ряд общих методов определения оценок и доверительных границ — метод моментов, метод максимального правдоподобия, метод одношаговых оценок, метод устойчивых (робастных) оценок, метод несмещённых оценок и другие. Кратко рассмотрим первые три из них. Теоретические основы различных методов оценивания и полученные с их помощью конкретные правила определения оценок и доверительных границ для тех или иных параметрических семейств распределений рассмотрены в специальной литературе, включены в нормативно-техническую и инструктивно-методическую документацию.
Метод моментов основан на использовании выражений для моментов рассматриваемых случайных величин через параметры их функций распределения. Оценки метода моментов получают, подставляя выборочные моменты вместо теоретических в функции, выражающие параметры через моменты.
В методе максимального правдоподобия, разработанном в основном Р. А. Фишером, в качестве оценки параметра θ берут значение θ * , для которого максимальна так называемая функция правдоподобия
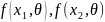 …
…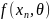
где 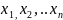 —
результаты наблюдений; f(x,θ) —
их плотность распределения, зависящая
от параметра θ, который нужно оценить.
—
результаты наблюдений; f(x,θ) —
их плотность распределения, зависящая
от параметра θ, который нужно оценить.
Оценки максимального правдоподобия, как правило, эффективны (или асимптотически эффективны) и имеют меньшую дисперсию, чем оценки метода моментов. В отдельных случаях формулы для них выписываются явно (нормальное распределение, экспоненциальное распределение без сдвига). Однако чаще для их нахождения надо численно решать систему трансцендентных уравнений (распределения Вейбулла-Гнеденко, гамма). В подобных случаях целесообразно использовать не оценки максимального правдоподобия, а другие виды оценок, прежде всего одношаговые оценки. В литературе их иногда не вполне точно называют «приближённые оценки максимального правдоподобия». При достаточно больши́х объёмах выборок они имеют столь же хорошие свойства, как и оценки максимального правдоподобия. Поэтому их следует рассматривать не как «приближённые», а как оценки, полученные по другому методу, не менее обоснованному и эффективному, чем метод максимального правдоподобия. Одношаговые оценки вычисляют по явным формулам
В
непараметрических задачах оценивания
принимают вероятностную модель, в
которой результаты наблюдений 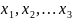 рассматривают
как реализации n независимых
случайных величин с функцией
распределения F(x) общего
вида. От F(x) требуют
лишь выполнения некоторых условий типа
непрерывности, существования
математического ожидания и дисперсии
и тому подобного. Подобные условия не
являются столь жёсткими, как условие
принадлежности к определённому
параметрическому семейству.
рассматривают
как реализации n независимых
случайных величин с функцией
распределения F(x) общего
вида. От F(x) требуют
лишь выполнения некоторых условий типа
непрерывности, существования
математического ожидания и дисперсии
и тому подобного. Подобные условия не
являются столь жёсткими, как условие
принадлежности к определённому
параметрическому семейству.
F - критерий Фишера используют для сравнения дисперсий двух вариационных рядов. Он вычисляется по формуле:
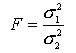 ,
,
где ![]() -
большая дисперсия,
-
большая дисперсия, ![]() -
меньшая дисперсия.
-
меньшая дисперсия.
Если вычисленное значение критерия F больше критического для определенного уровня значимости и соответствующих чисел степеней свободы для числителя и знаменателя, то дисперсии считаются различными.
Число степеней свободы числителя определяется по формуле:
![]() ,
,
где ![]() -
число вариант для большей дисперсии.
-
число вариант для большей дисперсии.
Число степеней свободы знаменателя определяется по формуле:
![]() ,
,
где ![]() -
число вариант для меньшей дисперсии.
-
число вариант для меньшей дисперсии.
