5. Метод по координатного спуску.

Потрібно мінімізувати функцію в області унімодальності. Вибираємо точку початкового спуска і будуємо послідовність наближень.

Нехай побудовано, тоді компонента наближення визначається за формулою:

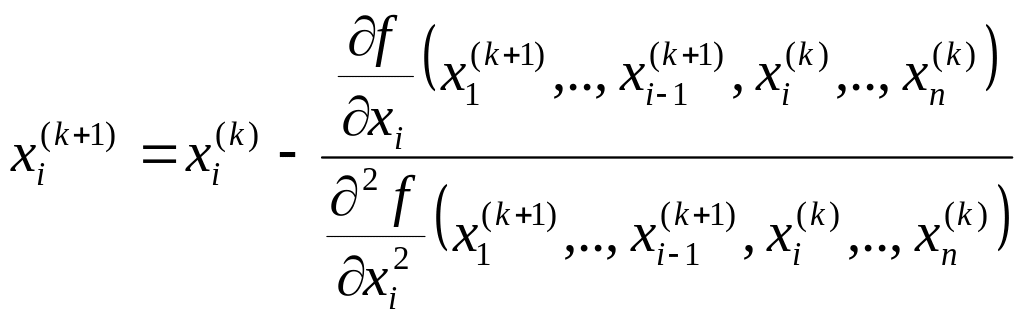
Процес побудови точок спуска закінчується, коли довжина градієнта менше заданої точності .

Для функції двох змінних координати точки спуску визначаються за формулами:

;

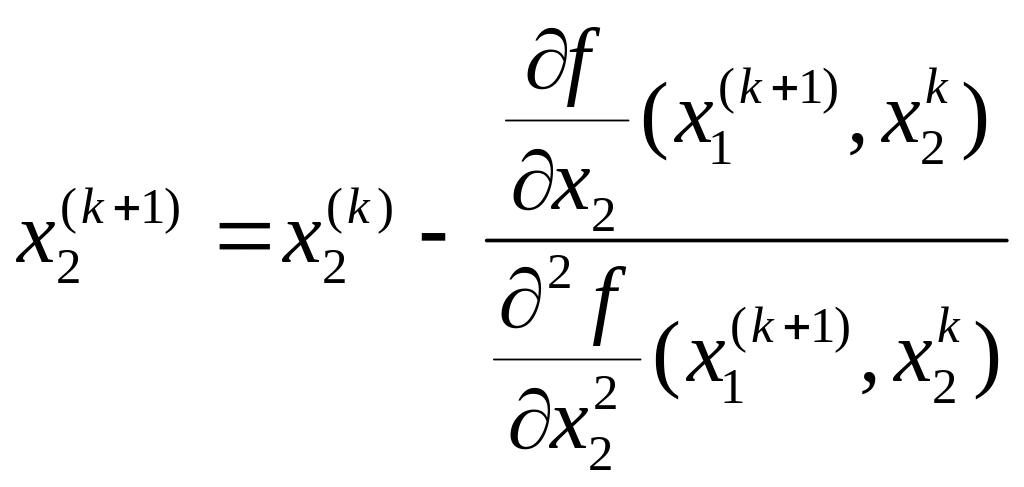
Питання для самоперевірки

1. Що називається точкою локального мінімуму функції декількох змінних?

2. Що називається градієнтом функції?

3. Як визначається аналітичне рішення?

4. Як будується ітераційний процес і вибирається напрямок спуску?

5. Який алгоритм методу найшвидшого градієнтного спуску?

6. Як визначається точка мінімуму за методом з дробленням кроку?

7. Як реалізується метод з постійним кроком?

8. Як знаходиться точка мінімуму за допомогою по координатного спуску?

Використовувана література

1. [1] стор. 192

2. [4] стор. 20-36

4. Лекція 4. Виведення формул чисельного диференціювання. Наближені методи рішення диференціних рівнянь першого порядку. Оцінка погрішності за правилом рунге. План лекції

1. Виведення формул чисельного диференціювання за допомогою многочлена Тейлора.

2. Постановка задачі для наближеного вирішення диференційних рівнянь першого порядку.

3. Метод Ейлера.

4. Погрішність наближеного рішення диференційних рівнянь, отриманих за методом Ейлера.

5. Метод «предиктор- коректор».

6. Вдосконалений метод Ейлера.

7. Метод Рунге - Кутта.

8. Правило Рунге для оцінки погрішності наближеного рішення диференційних рівнянь.

4.1 Виведення формул чисельного диференціювання.

Розглянемо функцію . Ставиться задача пошуку наближеного значення похідних першого та другого порядків цієї функції в точці .

Позначимо де Для виведення формул буде використаний ряд Тейлора.

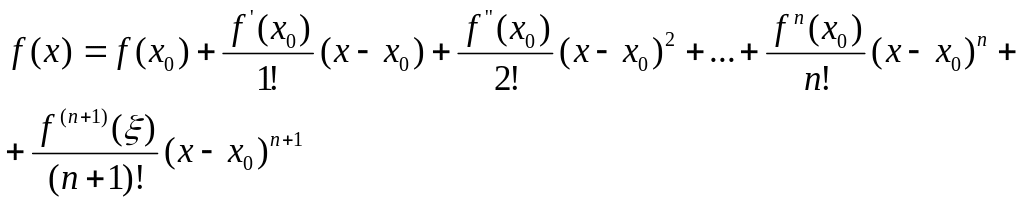
Позначимо

1) Хай на відрізку функція - функція, що двічі безперервно диференціюється, тоді існує точка така що

Вважаючи і враховуючи, що , одержуємо

, де .

Звідси

Різницева похідна першого порядку функції в точці визначається по формулі:

Погрішність формули: де .

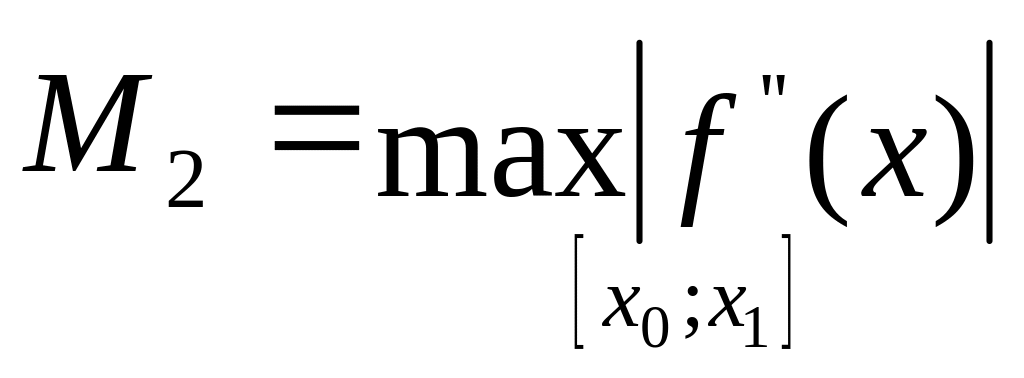Погрішність різницевої похідної має перший порядок точності відносно .

2) Хай функція тричі безперервно диференційована на відрізку . Ряд Тейлора має вигляд:

При , отримаємо

, де

При , отримаємо

, де

Знаходимо різницю

Використовуючи лему, отримаємо

, де

Тоді

Центральна різницева похідна першого порядку визначається за формулою:

Погрішність формули

, де

Погрішність центральної різницевої похідної має другий порядок точності відносно .

3) Хай функція чотири рази безперервно диференційована на . Ряд Тейлора має вигляд:

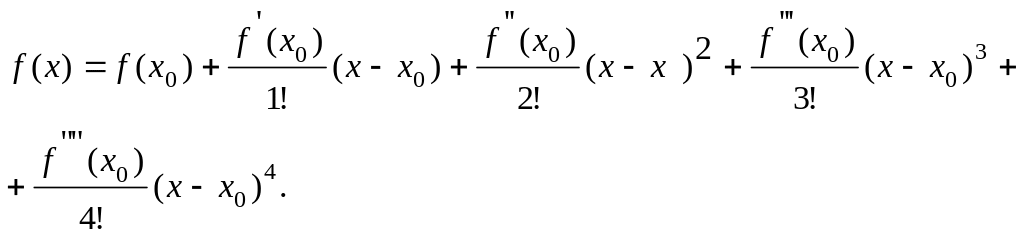
При , отримаємо

При , отримаємо

Складаємо формули:

Звідси виразимо

Різницева похідна другого порядку функції в точці визначається за формулою:

Погрішність формули

, де

Погрішність різницевої похідної має другий порядок точності відносно .

Можна вивести формули чисельного диференціювання, використовуючи многочлени Лагранжа і Ньютона.