Способы задания функций

Задать функцию означает установить правило (закон), с помощью которого по данным значениям независимой переменной следует находить соответствующие им значения функции. Рассмотрим некоторые способы задания функций.

Табличный способ. Довольно распространенный, заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством.

При табличном способе задания функции можно приближенно вычислить не содержащиеся в таблице значения функции, соответствующие промежуточным значениям аргумента. Для этого используют способ интерполяции.

Преимущества табличного способа задания функции состоят в том, что он дает возможность определить те или другие конкретные значения сразу, без дополнительных измерений или вычислений. Однако, в некоторых случаях таблица определяет функцию не полностью, а лишь для некоторых значений аргумента и не дает наглядного изображения характера изменения функции в зависимости от изменения аргумента.

Графический способ. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению.

Графический способ задания функции не всегда дает возможность точно определить численные значения аргумента. Однако он имеет большое преимущество перед другими способами - наглядность. В технике и физике часто пользуются графическим способом задания функции, причем график бывает единственно доступным для этого способом.

Чтобы графическое задание функции было вполне корректным с математической точки зрения, необходимо указывать точную геометрическую конструкцию графика, которая, чаще всего, задается уравнением. Это приводит к следующему способу задания функции.

Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим.

Этот способ дает возможность по каждому численному значению аргумента x найти соответствующее ему численное значение функции y точно или с некоторой точностью.

Если зависимость между x и y задана формулой, разрешенной относительно y, т.е. имеет вид y = f(x), то говорят, что функция от x задана в явном виде.

Если же значения x и y связаны некоторым уравнением вида F(x,y) = 0, т.е. формула не разрешена относительно y, что говорят, что функция y = f(x) задана неявно.

34

• Нечётная функция — функция, меняющая знак при изменении знака независимого переменного (симметричная относительно центра координат).

• Чётная функция — функция, не изменяющая своего значения при изменении знака независимого переменного (симметричнаяотносительно оси ординат).

• График четной функции. График нечетной функции.

• Графики четной и нечетной функций обладают следующими особенностями: Если функция является четной, то ее график симметричен относительно оси ординат.

• 

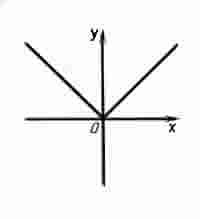
• Если функция является нечетной, то ее график симметричен относительно начала координат.

• 

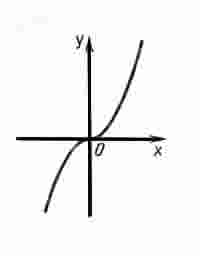
35

Периоди́ческая фу́нкция ― функция, повторяющая свои значения через какой-то ненулевой период, то есть не меняющая своего значения при добавлении к аргументу фиксированного ненулевого числа (периода).

36

Если поменять ролями аргумент и функцию, то  x  станет функцией от  y. В этом случае говорят о новой функции, называемой обратной функцией. Предположим, мы имеем функцию:

 

v = u ² ,

 

где  u - аргумент, a  v - функция. Если поменять их ролями, то мы получим  u  как функцию  v :

Если обозначить аргумент в обеих функциях через  x , а функцию – через   y,  то мы имеем две функции:

каждая из которых является обратной по отношению к другой.

 

П р и м е р ы .  Эти функции являются обратными друг к другу:

                        

1)  sin x  и  Arcsin x,  так как, если  y = sin x,  то   x = Arcsin y;

2)  cos x  и  Arccos x,  так как, если  y = cos x,  то  x = Arccos y;

3)  tan x  и  Arctan x,  так как, если  y = tan x,  то   x = Arctan y;

4)  e^x  и  ln x,  так как, если  y = e^x ,  то  x = ln y.

37

ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ – функция вида y = f(x), x  N,где N – множество натуральных чисел (или функция натурального аргумента), обозначается y = f(n) или y1, y2,…, y_n,…. Значения y1, y2, y3,…называют соответственно первым, вторым, третьим, … членами последовательности.

Числовая последовательность – частный случай числовой функции, поэтому ряд свойств функций рассматриваются и для последовательностей.

Определение. Последовательность {y_n} называют возрастающей, если каждый ее член (кроме первого) больше предыдущего:

y1 < y2 < y3 < … < y_n < y_n+1 < ….

Определение. Последовательность {y_n} называют убывающей, если каждый ее член (кроме первого) меньше предыдущего:

y1 > y2 > y3 > … > y_n > y_n+1 > … .

Возрастающие и убывающие последовательности объединяют общим термином – монотонные последовательности.

Пример 1. y1 = 1; y_n = n2\shad \shad0– возрастающая последовательность.

Пример 2. y1 = 1;   – убывающая последовательность.

Пример 3. y1 = 1;   – эта последовательность не является не возрастающей не убывающей.

Определение. Последовательность называется периодической, если существует такое натуральное число T, что начиная с некоторого n, выполняется равенство y_n = y_n+T . Число T называется длиной периода.

Пример. Последовательность   периодична с длиной периода T= 2.