42 Вопрос

Поверхностные интегралы первого рода

Рассмотрим скалярную функцию и поверхность S. Пусть S задана векторной функцией

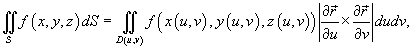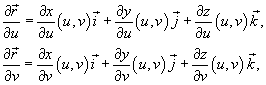где координаты (u,v) изменяются в пределах некоторой области определения в плоскости uv. Заметим, что функция рассматривается только в точках, принадлежащих поверхности S, то есть Поверхностный интеграл первого рода от функции по поверхности S определяется следующим образом: где частные производные и равны а означает векторное произведение. Вектор перпендикулярен поверхности в точке . Абсолютное значение 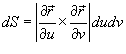называется элементом площади: оно соответствует изменению площади dS в результате приращения координат u и v на малые значения du и dv (рисунок 1).

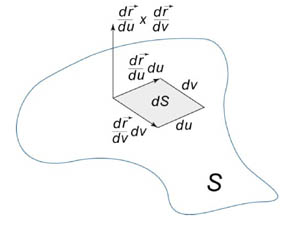
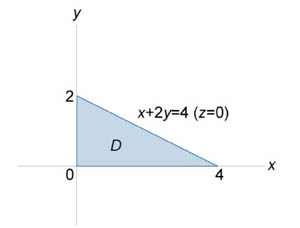
Рис.1 Рис.2

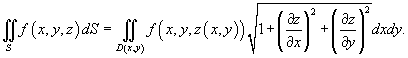Площадь поверхности S выражается с помощью поверхностного интеграла в виде Если поверхность S задана уравнением , где z (x,y) − дифференцируемая функция в области D (x,y), то поверхностный интеграл находится по формуле Если поверхность S состоит из нескольких частей Si, то для вычисления поверхностного интеграла можно использовать свойство аддитивности:

Скалярное и векторное поле. Циркуляция векторного поля вдоль кривой. Формула Грина. Если в каждой точке М определенной пространственной области задано значение некоторой скалярной или векторной величины, то говорят, что задано поле этой величины (соответственно скалярное или векторное).

43 Вопрос

Поверхностный интеграл второго рода

[править] Определение

Рассмотрим двустороннюю поверхность , гладкую или кусочно-гладкую, и фиксируем какую-либо из двух ее сторон, что равносильно выбору на поверхности определенной ориентации.

Для определенности предположим сначала, что поверхность задана явным уравнением причем точка изменяется в области на плоскости , ограниченный кусочно-гладким контуром.

Пусть теперь в точках данной поверхности определена некоторая функция . Разбив поверхность сетью кусочно-гладких кривых на части и выбрав на каждой такой части точку вычисляем значение функции в данной точке и умножим его на площадь проекции на плоскость элемента , снабженную определенным знаком. Составим интегральную сумму:

.

Конечный предел этой интегральной суммы при стремлении диаметров всех частей к нулю называют поверхностным интегралом второго рода от

,

распространенным на выбранную сторону поверхности , и обозначают символом

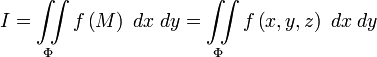
(здесь ) напоминает о площади проекции элемента поверхности на плоскость

Если вместо плоскости спроектировать элементы поверхности на плоскость или , то получим два других поверхностных интеграла второго типа:

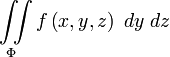или .

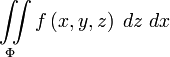В приложениях чаще всего встречаются соединения интегралов всех этих видов:

где суть функции от , определенные в точках поверхности .

[править] Связь между поверхностными интегралами второго и первого рода

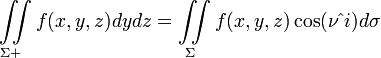, где — единичный вектор нормали поверхности , — орт.

[править] Свойства

1. Линейность: ;

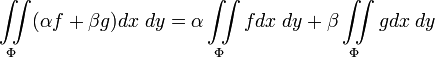2. Аддитивность: ;

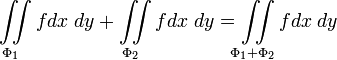3. При изменении ориентации поверхности, поверхностный интеграл меняет знак.