14 Билет.

Нормальное распределение, также называемое гауссовским распределением или распределением Гаусса —распределение вероятностей, которое задается функцией плотности распределения:

где параметр μ — среднее значение (математическое ожидание) случайной величины и указывает координату максимума кривой плотности распределения, а σ² — дисперсия.

Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1.

Биномиа́льное распределе́ние в теории вероятностей — распределение количества «успехов» в последовательности из   независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них равна  .

Пусть   — конечная последовательность независимых случайных величин с распределением Бернулли, то есть

Построим случайную величину  :

.

Тогда  , число единиц (успехов) в последовательности  , имеет биномиальное распределение с  степенями свободы и вероятностью «успеха»  . Пишем: Y∼Bin(n,p). Её функция плотности вероятности задаётся формулой:

где   — биномиальный коэффициент.

Распределение Ма́ксвелла — распределение вероятности, встречающееся в физике и химии. Оно лежит в основании кинетической теории газов, которая объясняет многие фундаментальные свойства газов, включая давление и диффузию. Распределение Максвелла также применимо для электронных процессов переноса и других явлений. Распределение Максвелла применимо к множеству свойств индивидуальных молекул в газе. О нём обычно думают как о распределении энергий молекул в газе, но оно может также применяться к распределению скоростей, импульсов, и модуля импульсов молекул. Также оно может быть выражено как дискретное распределение по множеству дискретных уровней энергии, или как непрерывное распределение по некоторому континууму энергии.

Распределение энергии Максвелла может быть выражено как дискретное распределение энергии:

,

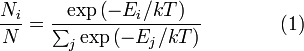Статистика Максвелла — Больцмана — статистический метод описания физических систем, содержащих большое число невзаимодействующих частиц, движущихся по законам классической механики (то есть классического идеального газа); предложена в 1871 г. австрийским физиком Л. Больцманом.

15 Билет.

Необратимый процесс, в результате которого в физической системе происходит пространственный перенос электрического заряда, массы, импульса, энергии, энтропии или какой-либо другой физической величины; описывается кинетическими уравнениями.

 Внутреннее трение (вязкость). Суть механизма возникновения внутреннего трения между параллельными слоями газа (жидкости), которые движущутся с различными скоростями, есть в том, что из-за хаотического теплового движения осуществляется обмен молекулами между слоями, в результате чего импульс слоя, который движется быстрее, уменьшается, который движется медленнее — увеличивается, что приводит к торможению слоя, который движется быстрее, и ускорению слоя, который движется медленнее. 

Как известно, сила внутреннего трения между двумя слоями газа (жидкости) подчиняется закону Ньютона:   (5)  где η — динамическая вязкость (вязкость), dν/dx — градиент скорости, который показывает быстроту изменения скорости в направлении х, перпендикулярном направлению движения слоев, S — площадь, на которую действует сила F.  Согласно второму закону Ньютона взаимодействие двух слоев можно рассматривать как процесс, при котором в единицу времени от одного слоя к другому передается импульс, который по модулю равен действующей силе. Тогда выражение (5) можно записать в виде   (6)  где j_p — плотность потока импульса — величина, которая определяется определяемая полным импульсом, переносимым в единицу времени в положительном направлении оси х через единичную площадку, перпендикулярную оси х, dν/dx — градиент скорости. Знак минус говорит о том, что импульс переносится в направлении убывания скорости (поэтому знаки j_p и dν/dx противоположны).  Динамическая вязкость η численно равна плотности потока импульса при градиенте скорости, равном единице; она вычисляется по формуле   (7)