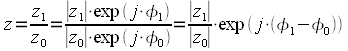Комплексное число

Ко́мпле́ксные^[1] чи́сла (устар. Мнимые числа^[2]), — расширение множества вещественных чисел, обычно обозначается  . Любое комплексное число может быть представлено как формальная сумма x + iy, где x и y — вещественные числа, i — мнимая единица^[3].

Комплексные числа образуют алгебраически замкнутое поле — это означает, что многочлен степени n с комплексными коэффициентами имеет ровно n комплексных корней (основная теорема алгебры). Это одна из главных причин широкого применения комплексных чисел в математических исследованиях. Кроме того, применение комплексных чисел позволяет удобно и компактно сформулировать многие математические модели, применяемые в математической физике и в естественных науках — электротехнике, гидродинамике, картографии, квантовой механике, теории колебаний и многих других.

Определения

Поле комплексных чисел можно понимать как расширение поля вещественных чисел, в котором многочлен z² + 1 имеет корень. Следующие две элементарные модели показывают, что непротиворечивое построение такой системы чисел возможно. Оба приведенных определения приводят к изоморфным расширениям поля вещественных чисел  , как и любые другие конструкции поля разложения многочлена z² + 1.

Операции над комплексными числами. Сложение комплексных чисел

Сумма двух комплексных числел   и   есть также комплексное число  :

.

(17)

Как следует из выражения (17) при сложении реальные и мнимые части комплексного числа также складываются.

На комплексной плоскости операцию сложения можно реализовать как сложение векторов комплексных чисел по правилу параллелограмма (рисунок 3).

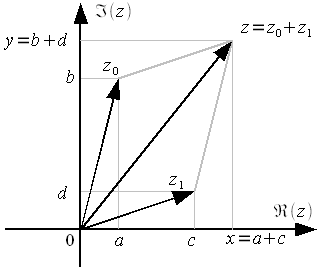Рисунок 3: Сложение комплексных чисел

Операции над комплексными числами. Вычитание комплексных чисел

Разность двух комплексных числел  и   есть также комплексное число  :

.

(18)

Как следует из выражения (18) при вычитании реальные и мнимые части комплексного числа также вычитаются.

На комплексной плоскости операцию вычитания можно реализовать как вычитание векторов комплексных чисел по правилу параллелограмма (рисунок 4). На первом шаге из вектора   формиуется вектор   после чего вектор   складывается с вектором   по правилу параллелограмма.

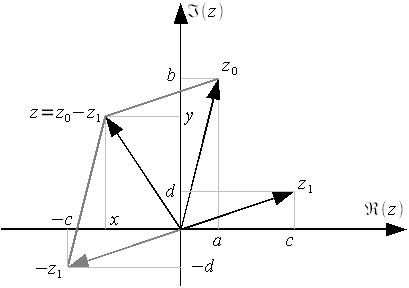Рисунок 4: Вычитание комплексных чисел

5)

УМНОЖЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ.СВОЙСТВА УМНОЖЕНИЯ.ДЕЛЕНИЕ.

Умножение комплексных чисел.

Определеие произведения комплексных чисел устанавливается с таким расчетом, чтобы числа a + b·i и a′ + b′·i можно было перемножать как алгебраические двухчлены, и чтобы число i обладало свойством i^2=−1. Произведение комплексных чисел a + b·i, и a′ + b′·i равно:

(a+bi)·(a′+b′i) = (a·a′−b·b′)+(a·b′+b·a′)i.

Деление комплексных чисел.

Устанавливается следующее определение. Разделить комплексное число a + b·i (делимое) на комплексное число a′ + b′·i (делитель) - значит найти такое число x + y·i (частное), которое, будучи помножено на делитель, даст делимое.

Если делитель не равен нулю, то деление всегда возможно и частное единственно.

Частное комплексных чисел a + b·i, и a′ + b′·i вычисляется по формуле:

a+b·i/a′+b′·i = a·a′−b·b′/a′^2+b′^2 + (a′·b−b′·a)*i/a′^2+b′^2.

Операции над комплексными числами. Умножение комплексных чисел

Для того чтобы получить формулу для умножения комплексных числен необходимо перемножить два комплексных числа по правилу умножения многочленов:

(19)

Таким образом получили также комплексное число. Умножать в явном виде комплексные числа не очень удобно, гораздо проще если привести их по формуле Эйлера к показательной форме:

.

(20)

При перемножении в показательной форме модули комплексных числел перемножаются а фазы складываются. На векторной диаграмме это можно представить следующим образом (рисунок 5):

Рисунок 5: Умножение комплексных чисел

При перемножении результирующий вектор поворачивается и его длина изменяется.

Исходя из выражения (15), умножение комплексного числа на чисто мнимое число приводит к повороту вектора на 90 градусов против часовой стрелки (к фазе   прибавляется 90 градусов). При этом из выражения (16) следует что умножение комплексного числа на -1 приводит повороту фазы на угол 180 градусов (вектор отражается относительно 0). Это очень важное замечание, так как емкости и индуктивности имеют чисто мнимые споротивления и служат для поворота вектора комплесного сигнала, в то же время поворот фазы на 180 градусов позволяет сформировать фазоманипулированные сигналы.

Операции над комплексными числами. Деление комплексных чисел

Последняя операция которую осталось рассмотреть — операция деления комплексных чисел. Рассмотрим деление в показательной форме:

(23)

Таким образом при делении комплексных чисел их модули делятся а фазы вычитаются. При делении необходимо чтобы . Получим формулу для деления комплексных чисел в явной форме. Пусть

(24)

умножим и числитель и знаменатель дроби на число комплексно-сопряженное знаменателя:

.

(25)

Исходя из (22) в знаменателе дроби получим квадрат модуля знаменателя а числитель перемножим по правилу умножения комплексных чисел:

.

(26)

Поделив почленно реальную и мнимую часть числителя на знаменатель получим:

.

(27)

Выражение (27) - формула деления комплексных чисел в явной форме. Как можно заметить операции сложения и вычитания удобнее выполнять в явном виде, тогда как умножать и делить комплексные числа быстрее и легче в показательной форме.