11.3 Метод фазовой плоскости

Состояние любой системы автоматического регулирования может быть определено значениями регулируемой координаты х и п—1 ее производных в n-мерном пространстве, называемом фазовым пространством системы. Это состояние харак­теризуется координатами изображающей точки в фазовом пространстве. В установившемся режиме системы, изображающая точка занимает фиксированное положение и называется особой точкой. В переходном режиме координаты точки будут меняться, образуя фазовую траекторию. Полная совокупность фазовых траекторий, соответствующая всем возможным начальным условиям, называется фазовым порт­ретом системы. Метод фазовой плоскости применяется для систем не выше третье­го порядка.

При изображении фазового портрета на плоскости уравнение второго порядка заменяется системой двух уравнений

Исключив из уравнения время, получим

Решение этого нелинейного дифференциального уравнения -определяет фазовую траекторию.

Пусть дано дифференциальное уравнение

корни этого уравнения

1) При а=0 (демпфирование=0).

Решение уравнения имеет вид , показывает, что в системе устанавливаются незатухающие гармонические колебания (рисунок 11.8). В случае чисто мнимых корней получим уравнение семейства фазовых траекторий, имеющих вид эллипсов. Изображающая точка движется по часовой стрелке, при незатухающих синусоидальных колебаниях описывает замкнутый контур (рисунок 11.8).

Рисунок 11.8 – Фазовая траектория для случая а=0

2) При положительном демпфировании а>0 и условии а²<4b получим комплексно-сопряженные корни. Переходный процесс в этом случае описывается уравнением и имеет затухающий характер. Фазовые траектории представляют собой логарифмические спирали, которые сходятся к одной особой точке, называемой устойчивым фокусом (0) (рисунок 11.9).

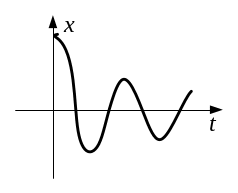
Рисунок 11.9 – Фазовая траектория при а>0

3) При отрицательном демпфировании а<0 возникают колебания с возрастающей амплитудой, характеризующие неустойчивый процесс. Переходный процесс описывается уравнением фазовые траектории в этом случае имеют вид логарифмиче­ских спиралей, но раскручивающихся из начала координат, которые представляет особую точку называемую неустойчивым фокусом (рисунок 11.10).

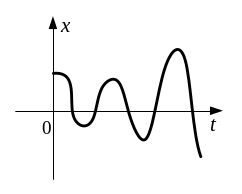
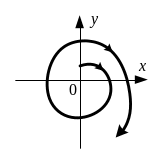
Рисунок 11.10 – Фазовая траектория при а<0

4) Если корни характеристического уравнения вещественны и от­рицательны, то переходный процесс описывается уравнением и имеет устойчивый апериодический характер. Начало координат - устойчивый узел. Отсутствуют колебания относительно точки равновесия (рисунок 11.11).

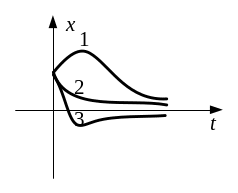
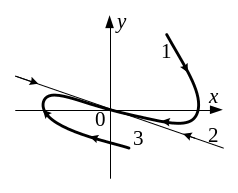
Рисунок 11.11 – Фазовая траектория при вещественных отрицательных корнях

5) При вещественных положительных корнях получим неустойчивый апериодический процесс. Начало координат - неустойчивый узел (рисунок 11.12).

Рисунок 11.12 – Фазовая траектория при вещественных положительных корнях

6) При вещественных корнях разных знаков получаем семейство фазовых траекторий, изображенных на рисунке 11.13. Начало координат – седло - особая точка.

Рисунок 11.13 – Фазовые траектории при вещественных корнях разных знаков

Рассмотренные фазовые портреты нелинейной системы второго порядка показывают, что по характеру фазовых траекторий можно судить об устойчивости движения системы.

С помощью метода фазовой плоскости могут быть решены сле­дующие задачи:

1. определение числа предельных циклов;

2. выявление критического соотношения параметров систе­мы, соответствующего области устой­чивости и автоколебаний;

3. анализ устойчивости в большом и состояний равновесия;

4. определение условий возникновения авто­колебаний;

5. определение параметров автоколебаний - амплитуды и частоты;

6. выявление качественной и количественной картины переходных процессов.

Решение этих задач может быть выполнено путем много­кратного построения фазовых портретов при разных значениях параметров.