Числа Фибоначчи

Это классический пример, который приводят почти везде, где речь идет о решении рекуррентных соотношений. Рассмотрим рекуррентное соотношение для чисел Фибоначчи:

Это хорошо известная последовательность, каждый элемент которой (кроме нулевого и первого) равен сумме двух предыдущих:

Эти числа очень быстро растут, например, f₁₀=55, f₂₀=6765, f₃₀=832040, f₁₀₀=354224848179261915075.

Первый шаг алгоритма мы уже выполнили, записав рекуррентное соотношение. Выполним второй шаг:

Складываем все строчки:

Третий шаг алгоритма требует привести все суммы к замкнутому виду:

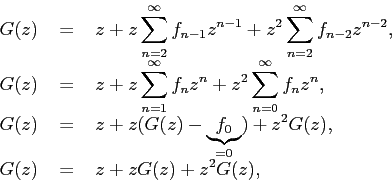
откуда получаем замкнутое выражение для производящей функции:

Осталось «всего лишь» разложить её в ряд (чего требует четвёртый шаг алгоритма). С этой целью нужно разложить знаменатель на множители. Найдем корни уравнения:

Таким образом (проверьте),

Как теперь поступить с этими выражениями? Ведь пока нам известно разложение только одной рациональной функции:

Рассмотрим первую дробь и поделим в ней числитель и знаменатель на z₁:

Аналогично (но с делением на z₂) поступим со второй дробью:

Таким образом,

и, следовательно,

Данное выражение можно «причесать», если обратить внимание на то, что 1/z₁=-z₂, 1/z₂=-z₁ и z₁-z₂=√5 (корень из 5):

Если записывать формулу в терминах хорошо известного «золотого сечения»

то, обозначив , получим

Если «золотое сечение» не использовать, то лучше всего формула выглядит в следующем виде:

чего достаточно трудно было ожидать, глядя на красивое исходное рекуррентное соотношение.

Обязательно проверьте формулу хотя бы для n=0, 1, 2. Как изменится производящая функция и конечная формула, если положить f₀=f₁=1?

32. Общая схема решения рекуррентного соотношения с помощь производящих функций на примере решения рекуррентного соотношения , , , .

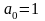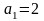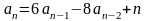Рассмотрим довольно произвольное рекуррентное соотношение:

Рассчитаем несколько первых элементов:

Несколько следующих действий мы выполним без пояснений, поскольку они абсолютно аналогичны тем, которые уже делались раньше:

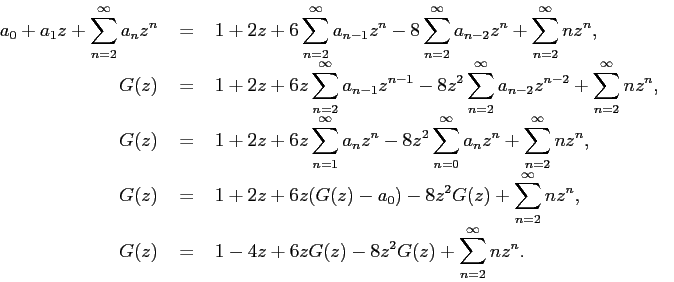
Пока непонятно, что делать с последней суммой. Как её «замкнуть»? На самом деле, очень просто, если вспомнить про производную (подробнее см. лекцию «Преобразование производящих функций: полиномиальный множитель и делитель»):

поэтому

Обратите внимание, что мы вынесли производную за знак бесконечной суммы, не проверив, имеем ли мы на это право. Можно показать, что все сделано законно, но мы не будем этим заниматься сейчас. Последняя сумма может быть свёрнута:

Подставив свёрнутое выражение обратно, имеем,

Таким образом, наше последнее уравнение примет вид

Это уравнение для производящей функции. Из него выражаем G(z):

Довольно страшное выражение, которое нам предстоит разложить в ряд, на самом деле только кажется таким. Разложим знаменатель на множители и разобьём дробь на сумму простых дробей:

Дальше мы знаем что делать со всеми этими дробями, кроме, разве лишь, первой. Рассмотрим её (без множителя) подробнее (см. также «Расширенные биномиальные коэффициенты»):

Теперь соберём ответ:

Значит,

Подстановка первых пяти значений совпадает с числами из таблицы, в которую мы их записали в начале.

33. Переключательные (булевы) функции. Происхождение булевых функций.

Для формального описания узлов ЭВМ при их анализе и синтезе используется аппарат алгебры логики. Основные положения алгебры логики разработал в XIX в. английский математик Джордж Буль. Алгебру логики называют также булевой алгеброй. В булевой алгебре различают двоичные переменные и булевы функции. Двоичные переменные могут принимать два значения: 0 и 1. Они называются также логическими или булевыми переменными и обозначаются символами x₁, x₂, x₃,… Булевы функции зависят от двоичных переменных. Они, как и аргументы, могут принимать лишь два значения: 0 или 1. Булевы функции называют также логическими или переключательными функциями. Будем обозначать переключательные функции в виде f(x₁, x₂, x₃, …) указывая в скобках аргументы, либо в виде y₁, y₂, y₃,… Булевы функции в свою очередь могут служить аргументами еще более сложных логических функций. Следовательно, можно построить переключательные функции любой заранее заданной сложности, пользуясь ограниченным числом логических связей. Булевы функции принято задавать таблицами истинности, в которых для всех наборов переменных указываются соответствующие им значения булевых функции. Формирование значений в таблице истинности выполняется в соответствии с логикой работы устройства (сумматора, сдвигателя, преобразователя кодов и т. д.). Набор переменных — это совокупность значений двоичных переменных, каждая из которых может быть равна 0 или 1. Если число аргументов (независимых переменных) переключательных функций равно n (т. е.x₁, x₂, x₃,…x_n), то существует два различных сочетаний этих переменных, т. е. наборов.