Министерство Образования Российской Федерации

Тверской Государственный Технический Университет

Кафедра "Информационные системы"

МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ЗАДАНИЯ

К КОНТРОЛЬНЫМ РАБОТАМ

по курсу

«ЭКОНОМЕТРИКА»

Тверь,2003

Предмет эконометрики и ее основные задачи

Эконометрика – раздел эконометрики, занимающейся разработкой и применением статистических методов для измерения взаимосвязей между эконометрическими переменными.

Эконометрика – единство трёх составляющих:

– статистики,

– экономической теории,

– математики.

Основные результаты экономической теории носят качественный характер, а эконометрика вносит в них эмпирическое (опытное) содержание.

Математика выражает математические законы в виде математических соотношений. Эконометрика осуществляет проверку этих законов.

Статистика дает информационное обеспечение исследуемого процесса в виде исходных статистических данных и показателей. Эконометрика проверяет количественные взаимосвязи между эмпирическими показателями.

Показатели разделяются на два вида:

– результирующие (зависимые),

– факторные (независимые, предикатные, объясняющие), то есть те, от которых зависят результирующие показатели.

Основная задача: получить (определить) ожидаемое значение зависимой переменной при заданных значениях объясняющих переменных.

Наблюдаемое значение результирующей переменной зависит не только от факторных переменных, но и от случайных явлений, определяемых другими неучтенными факторами.

Общим моментом для любой эконометрической модели является разбиение зависимой переменной на две части:

– объясняющую (детерминируемую)

– случайную.

Таким образом, основную задачу моделирования можно сформулировать следующим образом:

На основании эмпирических данных определить объясненную часть и, рассматривая случайную составляющую как случайную величину, получить оценки параметров ее распределения.

Линейный регрессионный анализ

В линейный регрессионный анализ входит широкий круг задач, свя­занных с построением (восстановлением) зависимостей между группами чи­словых переменных

Предполагается, что X - независимые переменные (факторы, объяс­няющие переменные) влияют на значения Y - зависимых переменных (результирующих, объясняемых переменных). По имеющимся эмпирическим данным (x_i, y_i), i = 1,...,n (n – число наблюдений) требуется построить функцию f(X), которая приближенно описывала бы изменение Y при изменении X:

Предполагается, что множество допустимых функций, из которого подбирается f(X), является параметрическим:

f(X) =f(X, ),

где  - неизвестный параметр (вообще говоря, многомерный). При построении f(X) будем считать, что

Y = f(X, )+, (1)

где первое слагаемое - закономерное изменение Y от X, а второе -  - случай­ная составляющая с нулевым средним. f(X, ) является условным математическим ожиданием Y при условии известного X и называется рег­рессией Y no X.

Простая линейная регрессия

Пусть X и Y одномерные величины; обозначим их х и .у, а функция f(x,) имеет вид f(x,) = a+bx, где  = (a, b). Относительно имеющихся наблюдений (x_i, y_i), i = 1,..., n, полагаем, что

y_i = a + bx_i + _i (2)

где ₁,…_n- независимые одинаково распределенные случайные величины, определяющие действие различных неучтенных факторов на изменение результирующего показателя Y.

Уравнение (2) определяет простую (парную) линейную регрессию. Можно различными методами подбирать "лучшую" прямую линию, изменяя параметры a и b. На практике широко используется метод наименьших квадратов (МНК), суть которого заключается в следующем.

По­строим оценку параметра  = (a, b) так, чтобы величины

e_i = y_i – f(x_i, ) = y_i – a - bx_i

называемые остатками, были как можно меньше, а именно, чтобы сумма их квадратов была минимальной:

(3)

Сумму минимимизируем по (а,b), приравнивая нулю производные по а и b. В результате получим систему уравнений линейных относительно a и b. Ее решение легко находится:

(4) и (5)

Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции r_yx. Для линейной регрессии (-1≤r_yx≤1)

r_yx = bσ_x/σ_y

σ_{x =} , σ_{y =}

и индекс корреляции ρ_yx – для нелинейной регрессии (0≤ρ_yx≤1)

ρ_yx = , ,

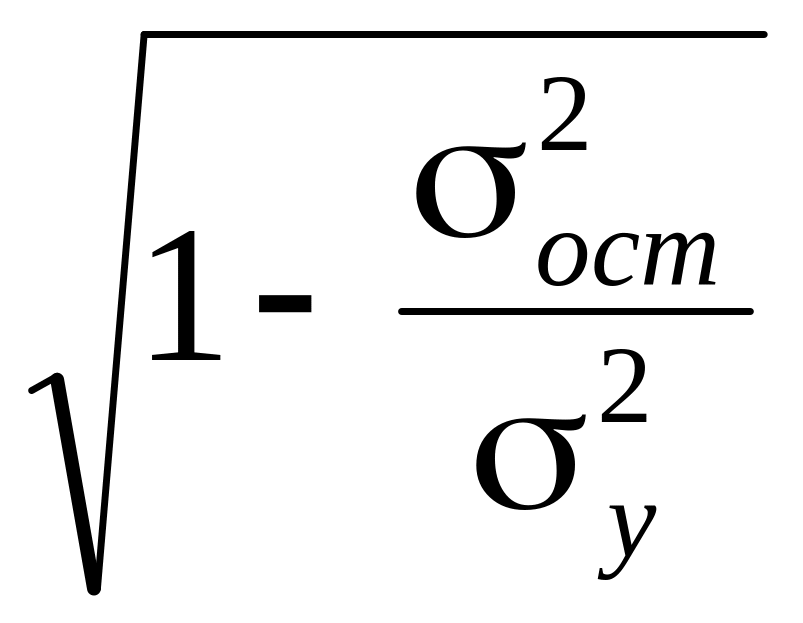где - дисперсия результирующего показателя y; - дисперсия отклонений наблюдаемых значений результирующего показателя y_i от рассчитанных по уравнению регрессии .

Качество построенной модели можно оценить с помощью коэффициента (индекса) детерминации:

R² = = = ρ²_yx,

здесь - дисперсия, объясняемая регрессией. Чем больше значение этого показателя ( а оно изменяется от 0 до 1), тем лучше уравнение регрессии объясняет рассеяние наблюдаемых значений результирующего показателя y относительно средней величины, тем меньшее влияние на это рассеяние оказывают случайные факторы. Это видно из соотношения:

Задача дисперсионного анализа состоит в анализе дисперсии результирующего показателя.

Для получения несмещенной оценки дисперсии случайной величины сумму квадратов отклонений от среднего значения делят не на число наблюдений – n, а на число степеней свободы – df.

Число степеней свободы равно разности между числом неизвестных наблюдений случайной величины и числом связей, ограничивающих свободу их изменений, т. е. числом уравнений, связывающих эти наблюдений.