МАТЕМАТИЧЕСКИЙ АНАЛИЗ.

Тема 1.

1. Определения.

1.1. Ограниченным множество вещ. чисел называется множество, ограниченное сверху и снизу. .

1.2. Ограниченное сверху множество: .

1.3. Ограниченное снизу множество: .

1.4. Неограниченным множество вещ. чисел .

1.5. Неограниченное сверху множество: .

1.6. Неограниченное снизу множество: .

1.7. Окрестностью данной точки называется любой интервал, содержащий эту точку.

1.8. -окрестностью точки с называется интервал

1.9. Проколотой -окрестностью называется множество

1.10. точка а называется предельной точкой множества Х, если содержит точки множества Х .

1.11. Верхней гранью множества Х называется число [наименьшее число, ограничивающее это множество сверху]

1.12. Нижней гранью множества Х называется число [наибольшее число, ограничивающее это множество снизу]

1.13. Точной верхней гранью ограниченного множества Х называется наименьшая из его верхних граней.

1.14. Точной нижней гранью ограниченного множества Х называется наибольшая из его нижних граней.

1.15. Если каждому n числу N поставить в соответствие некоторое число , то говорят, что определена числовая последовательность.

1.16. Последовательность { называется ограниченной, если

1.17. Последовательность { называется неограниченной, если

1.18.

1.19. Число а называется пределом последовательности , если .

1.20. Последовательность называется бесконечно малой, если

1.21. Последовательность называется бесконечно большой, если .

1.22. Последовательность называется фундаментальной, если .

1.23. Пусть { - некоторая числовая последовательность. Рассмотрим произвольную возрастающую последовательность чисел тогда 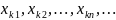- подпоследовательность последовательности .

1.24. 1 )Число а называется предельной точкой последовательности , если из можно выделить последовательность , сходящуюся к а. 2) Число а называется предельной точкой , если в точки а содержится бесконечно много членов .

1.25. Верхним пределом последовательности называется наибольшая предельная точка последовательности , ограниченной сверху.

1.26. Нижним пределом последовательности называется наименьшая предельная точка последовательности , ограниченной сверху.

Теоремы.

2.1. Теорема о пределе суммы, разности, произведения и частного двух последовательностей. А) ∑ сходящихся последовательностей и есть сходящаяся последовательность, предел которой равен сумме пределов последовательностей и . 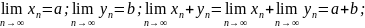Б) Разность: ; В) Произведение: ; Г) Частное двух сходящихся последовательностей и при условии, что , есть сходящаяся последовательность, предел которой равен частному пределов последовательностей и . .

2.2. Теорема «о двух милиционерах». Если и начиная с некоторого номера выполняются неравенства , то .

2.3. Теорема о пределе монотонной ограниченной последовательности. А) Если неубывающая (невозрастающая) последовательность ограничена сверху (снизу), то она сходится. Б) Если монотонная последовательность ограничена с обеих сторон, то она сходится.

2.4. Теорема о вложенных отрезках. Для всякой системы вложенных отрезков существует хотя бы 1 точка с, принадлежащая всем отрезкам данной системы. Если, кроме того, длина отрезков системы стремится к 0: 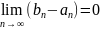, то с – единственная общая точка всех отрезков данной системы.

2.5. Теорема Больцано-Вейерштрасса. Из любой ограниченной последовательности можно выделить сходящуюся последовательность.

2.6. Критерий Коши сходимости последовательности. Для того, чтобы последовательность сходилась, необходимо и достаточно, чтобы она была фундаментальной.

ТЕМА 2

Определения.

1.1. Функция ограничена на Х, если

1.2. Функция ограничена сверху на множестве Х, если

1.3. Функция ограничена снизу на множестве Х, если

1.4.

1.5. Функция неограниченна сверху на множестве Х, если

1.6. Функция неограниченна снизу на множестве Х, если

1.7. Верхней гранью функции на множестве Х называется т. М, удовлетворяющая условию .

1.8. Если , то м называют нижней гранью функции на множестве Х.

1.9. Число М называют точной верхней гранью функции y=f(x) на множестве Х, если .

1.10. Число м называют точной верхней гранью функции y=f(x) на множестве Х, если .

1.11. Функция f(x) на промежутке Х называется: а) возрастающей; б) неубывающей; в) невозрастающей; г) убывающей, если , где а)-г) – монотонная ф-я; а),г) – строго монотонная ф-я.

1.12. Число в называется пределом функции f(x) в т а (при по Коши, если .

1.13. Число в называется правым пределом функции f(x) в т а (при по Коши, если .

1.14. Число в называется левым пределом функции f(x) в т а (при по Коши, если .

1.15. Число в называется пределом функции f(x) (при по Коши, если .

1.16. Число в называется пределом функции f(x) (при по Коши, если .

1.17. Число в называется пределом функции f(x) в т. а (при х->a) по Коши, если для любой сходящейся к а последовательности такой, что , соответствующая последовательность значений функции сходится к в.

1.18 Число в называется пределом функции f(x) при x-> по Гейне, если для любой б.б. последовательности соответствующая последовательность значений функции сходится к в..

1.19. Число в называется пределом функции f(x) при x->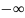 по Гейне, если для любой б.м. последовательности соответствующая последовательность значений функции сходится к в.

1.20.

1.21.

1.22. при по Коши если для

1.23. при по Коши если для

1.24. при по Коши если для

1.25. при по Коши если для

1.26. при по Коши если для (????????????????????????????????)

1.27. при по Коши если для (????????????)

1.28. - б.м. при по Коши если для

1.29. - б.м. при по Коши если для

1.30. при по Гейне. Функция f(x) – б.б., если для ∀ { , сходящейся к а: соответствует последовательности является б.б.

1.31. при по Гейне. Функция f(x) – б.б., при , если для ∀ б.б. последовательности { , соответствующая последовательность является б.б.

1.32. при по Гейне. Функция f(x) – б.б., при , если для ∀ б.м. последовательности { , соответствующая последовательность является б.б.

1.33. Функция называется непрерывной в т. а, если предельное значение этой функции в т. а существует и равно частному значению . [ ]

1.34. Непрерывной на промежутке функцией называется функция, непрерывная во всех внутренних точках, но на концах отрезка непрерывная справа и слева.

1.35. Точкой разрыва функции называется предельная т. х функции, в которой функция не является непрерывной.

1.36. Точка а называется точкой устранимого разрыва, если , то функция неограниченна в точке а, либо ее значение равно частному.

1.37. Точка а называется точкой разрыва 1 рода, если

1.38. Точка а называется точкой разрыва 2 рода, если в этой точке хотя бы 1 из односторонних пределов не существует или равен бесконечности.

1.39. Функция, которая каждому ставит в соответствие , называется обратной по отношению к функции

ТЕОРЕМЫ.

2.1. Критерий Коши существования предела функции при x->a. Для того, чтобы в т. А существовал предел, необходимо и достаточно, чтобы выполнялось условие

2.2. Критерий Коши существования предела функции при

2.3. О пределе (+), (-), (*), (/) двух функций. Если пределы существуют.

2.4. Связь предела функции в данной точке с односторонним пределом в данной точке. Если f(x) определена в некоторой окрестности т. А, кроме, быть может, самой точки а, и , то

2.5. О 1замечательном пределе:

2.6. О 2 замечательном пределе:

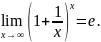
2.7. Теорема о непрерывности (+), (-), (*), (/) двух непрерывных функций. Пусть заданы на одном и том же множестве функции f(x) и g(x), имеют в точке а предельное значение в и с, тогда функции

2.8. Теорема о непрерывности сложной функции. Если функция непрерывна в т.а, а функция непрерывна в соответствующей точке , то сложная функция непрерывна в т. а.

2.9.