1.Числовые последовательности

Придел числовой последовательности – функция натурального аргумента f(n), где n=1,2,3… Придавая различные значения получим зн.функции в этих точках. Например: f(n)=1/n=1=1/2=1/3…

Определение: Число а наз.пределом последовательности а_1,а_2,а_n… ,если для любого положит.числа Е>0,сущ.такой номер(n), что для люб.номеров вып.неравенство│а_n-а│<E.

Св-ва:

1.Предел постоянной величины

Предел постоянной величины равен самой постоянной величине:

2.Предел произведения функции на постоянную величину

Постоянный коэффициент можно выносить за знак предела:

3.Предел суммы

Предел суммы двух функций равен сумме пределов этих функций:

4.Предел произведения

Предел произведения двух функций равен произведению пределов этих функций (при условии, что последние существуют):

5.Предел частного

Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:

2.Предел функции

Определение предела по Коши. Число A называется пределом функции f(x) в точке x = x₀, если для любого числа существует такое число , что для всех удовлетворяющих неравенству |x – x₀ | <δ, выполняется неравенство | f(x) – A | < ε.

Определение одностороннего предела.

Если Х>Х₀ (Х<Х₀), то пишут и называют А пределом ф-и в т.Х₀ справа(слева).

Св-ва:

1.Предел постоянной величины

Предел постоянной величины равен самой постоянной величине:

2.Предел произведения функции на постоянную величину

Постоянный коэффициент можно выносить за знак предела:

3.Предел суммы

Предел суммы двух функций равен сумме пределов этих функций:

4.Предел произведения

Предел произведения двух функций равен произведению пределов этих функций (при условии, что последние существуют):

5.Предел частного

Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:

3.Раскрытие неопределенностей 0/0.

Для того что бы раскрыть неопред. 0/0, необходимо разложить на множители числит. и знамен., сократить выр-е в числ.и знам. дающую данную неопред-ть и вычислить предел.

Раскрытие неопределенности ∞/∞.

Для того чтобы раскрыть неопред. ∞/∞, необходимо каждое слагаемое числит.и знам. разделить на высшую степень вход-ю в данное выр-е и вычислить предел.

4.Первый замечательный предел

lim sinx/x = 1 (x→ 0)

S сектора ОМК‹ОМК‹ОСК

1. S ОМК=1/2ОК*МВ=1/2*1*sin x=1/2 sin x

2. S сектора ОМК=1/2ОК*МК=1/2*1*Х=1/2Х

3. S ОСК=1/2ОК*СК=1/2tgx

1/2 sin x<1/2 x<tgx

Sinx<x<sinx/cosx │/sinx

1<x/sinx<1/cosx

1>sinx/x>cosx

Св-ва

1.

2.

3.

4.

5.Второй замечательный предел.

lim(х→+ ∞) (1+1/x)^x =e– второй замечательный предел.

6.Теорема о непрерывности элементарных функций (формулировка, примеры)

Опред. непрерывности ф-и в точке.

Рассм. ф-ю y=(x) на X. Пусть x₀ назыв. точкой непрерывности ф-и (x), если:

1. ф-я опред. в некоторой окрестности этой точки, включая саму точку, т.е. (x₀)

2. lim(x₀)

^xx0

3)lim(x)=(x₀)

^xx0

Можно дать опред. Непрерывности.ф-я (x) назыв. непрерывной в точке x₀, если:

1. она опред. в некот. окрестности этой точки, включ. саму точку

2. для >0 _>0: из 0<|x-x₀|<  |(x)-(x₀)|<0

Существует 3-е опред. непрерывности – опред. на языке приращения:

обозначим x–x₀=x

y–y₀=(x)­–(x₀)=y.

y=(x) называется непрерывной в точке x₀, если она опред. в некот. окрестности х_о, т.е. lim_x0

y=0.

Можно показать равносильность этих опред.

Введем понятие односторонних пределов ф-и.

Если (x),опред.в т.х=а и при этом lim _xa+0(x)= (а), то говорят что ф-я у=(x) в т.х=а непрерывна справа.

Если (x),опред.в т.х=в и при этом lim _xв-0(x)= (в), то говорят что ф-я у=(x) в т.х=в непрерывна слева.

Утверждение: для того, чтобы ф-я (x) имела конечный предел при xa, необходимо и достаточно равных конечных одностор. пределов.

Теорема:Пусть ф-ция f(x) и g(x) непрерывны в точке х₀. Тогда ф-ция f(x) g(x), f(x)*g(x), f(x)/g(x) также непрерывны в этой точке (последняя при g(x₀) 0)

Точки разрыва ф-ции.

1) Т. x₀ н/з т. р-ва ф-ции y=f(x), если эта т. принадлежит D(y) или её границе.

2) В этой т. нарушается непрерывность.

По характеру разрыва т. р-ва делятся следующим образом:

1) т. р-ва первого рода

а) точки устранимого р-ва

x₀ – т. устранимого р-ва, если односторонние пределы в этой т. конечны и равны, но не равны значению ф-ции в данной точке (которого может и не быть)

y= sin/x, x ≠ 0; x = 0 – т. р-ва

Вычислим односторонние пределы:

Lim sinx/x =1 (x→ + 0); Lim sinx/x =1 (x→ - 0), а следовательно они равны => f(x₀) – имеет устранимый р-в Можно создать непрерывную всюду ф-ю f(x) ={sinx/x; x ≠ 0 и 1; x=0

б) р-в 1-ого рода

x₀ – т. р-ва 1-ого рода, если односторонние пределы в этой т. конечны, но не равны.

y= sin/|x|, x ≠ 0; x = 0 – т. р-ва

Lim sinx/|x| =1 (x→ + 0); Lim sinx/x = -1 (x→ - 0)

Графически р-в изображается скачком по оси ординат.

3. Т. р-ва второго рода

x₀ – т. р-ва 2-ого рода, если хотя бы один из односторонних пределов = бесконечн. или не существуют.

7. Производная ф-и

производной функцией f(x) в.т.Х наз.предел отношения приращения ф-и к приращ.аргумента при x→0

Пример: y=x² y’=2x

y+∆y=(x+∆x)²

∆y=(x+∆x)²-y

∆y=x²+2x*∆x+(∆x)²-x²

∆y=2*x*∆x+(∆x)²

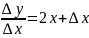
y’=2x

8.геометрический смысл производной

С геом.т.з. произв.ф.это tg угла наклона касательной с положит-м направлением оси Ох.

10. пр-я сл.ф

11. обратная ф-я

12.неявная ф-я

Правило

Для того чтобы продифференцировать неявную ф-ю нужно взять производную от левой и правой части по Х, считая, что У сложная функция от Х.

13. показ-степ.ф-я

Для того чтобы взять производную от показ-степ. ф.необходимо прологарифмировать лев.и прав.части, найти производную и выразить у′.

14.пр-я суммы…

15. теорема Ролля

16. т. Лагранжа

17.   Необходимое условие экстремума функции

18. Достаточные условия экстремума

правило. Если при переходе (слева направо) через критическую точку x0 производная f ' (x0) меняет знак с плюса на минус, то в точке x0 функция f (x) имеет максимум; если с минуса на плюс, то минимум; если знака не меняет, то экстремума нет.

19. достаточный признак экстремума

Первый достаточный признак экстремума функции

Если функция у=f(x) дифференцируема в окрестности стационарной точки х₀ и ее производная слева от этой точки положительная, а справа отрицательная, то в точке х₀ функция достигает максимума; если производная слева от стационарной точки х₀ отрицательная, а справа – положительная, то в точке х₀ функция достигает минимума; если производная слева и справа от стационарной точки х₀ имеет одинаковый знак, то в этой точке функция экстремума не имеет.

   Доказательство. Если производная f '(x) при переходе через x = x₀ меняет знак с "+" на "-", то это означает, что при достаточно малом h производная f '(x) положительна в интервале (x₀ - h, x₀ ) и отрицательна в интервале (x₀ , x₀ + h). Следовательно, функция f(x) в интервале (x₀ - h, x₀ ) возрастает, а в интервале (x₀ , x₀ + h) убывает, то есть в точке x₀ достигает максимума.    Аналогично доказывается утверждение данной теоремы относительно минимума функции.      Второй достаточный признак экстремума

Если в стационарной точке х₀ вторая производная отлична от нулю, то в этой точке функция у=f(x) имеет максимум при f '(x₀)<0 и минимум при f '(x₀)>0.

 Доказательство. Докажем необходимость условия существования максимума. Пусть f '(x) = 0,  f ''(x) > 0.    Так как f ''(x) непрерывна, то в достаточно малом интервале (x₀ - h, x₀ + h) вторая производная положительна: f ''(x) > 0. Это означает, что f '(x) возрастает в этом интервале. Так как при этом f '(x₀ )=0, то f '(x)<0 в интервале (x₀ - h, x₀ ) и f '(x)>0 в интервале (x₀  , x₀ + h).    Таким образом, функция f(x) убывает в интервале (x₀ - h, x₀ ) и возрастает в интервале (x₀  , x₀ + h). Поэтому в точке x₀ функция f(x) имеет минимум. Аналогично доказывается достаточность условия существования максимума. На рисунке функция f(x) имеет в точке x₁ минимум, в точке x₂ - максимум.

20.