Задание 1.8
Построить поверхности и определить их вид (название).
1. а) 4х2 - у2 - 16z2 + 16 = 0; б) х2 + 4z = 0.
2. а) 3х2 + у2 + 9z2 - 9 = 0; б) х2 + 2у2 - 2z = 0.
3. а) -5х2 + 10у2 - z2 + 20 = 0; б) у2 + 4z2 = 5х2.
4. а) 4х2 - 8у2 + z2 + 24 = 0; б) х2 - у = -9z2.
5. а) х2 - 6у2 + z2 = 0; б) 7х2 - 3у2 - z2 = 21.
6. а) z = 8 - х2 - 4у2; б) 4х2 + 9у2 + 36z2 = 72.
7. а) 4х2 + 6у2 - 24z2 = 96; б) у2 + 8z2 = = 20х2.
8. а) 4х2 - 5у2 - 5z2 + 40 = 0; б) у = 5х2 + 3z2.
9. а) х2 = 8(у2 + z2); б) 2х2 + 3у2 - z2 = 18.
10. а) 5z2 + 2у2 = 10х; б) 4z2 - 3у2 - 5х2 + 60 = 0.
11. а) х2 - 7у2 - 14z2 - 21 = 0; б) 2у = х2 + 4z2.
12. а) 6х2 - у2 + 3z2 - 12 = 0; б) 8у2 + 2z2 = х.
13. а) -16х2 + у2 + 4z2 - 32 = 0; б) 6х2 + у2 - 3z2 = 0.
14. а) 5х2 - у2 - 15z2 + 15 = 0; б) х2 + 3z = 0.
15. а) 6х2 + у2 + 6z2 - 18 = 0; б) 3х2 + у2 - 3z = 0.
16. а) -7х2 + 14у2 - z2 + 21 = 0; б) у2 + 2z2 = 6х2.
17. а) -3х2 + 6у2 - z2 - 18 = 0; б) х2 - 2у = -z2.
18. а) 4х2 - 6у2 + 3z2 = 0; б) 4х2 - у2 - 3z2 = 12.
19. а) z = 4 - х2 - у2; б) 3х2 + 12у2 + 4z2 = 48.
20. а) 4х2 + 5у2 - 10z2 = 60; б) 7у2 + z2 = 14х2.
21. а) 9х2 - 6у2 - 6z2 + 1 = 0; б) 15у = 10х2 + 6у2.
22. а) х2 = 5 (у2 + z2); б) 2х2 + 3у2 - z2 = 36.
23. а) 4х2 + 3у2 = 14х; б) 3х2 - 4у2 - 2z2 + 12 = 0.
24. а) 8х2 - у2 - 2z2 - 32 = 0; б) у - 4z2 = 3х2.
25. а) х2 - 6у2 + z2 - 12 = 0; б) х - 3z2 = 9у2.
26. а) 2х2 - 3у2 - 5z2 + 30 = 0; б) 2х2 + 3z = 0.
27. а) 7х2 + 2у2 + 6z2 - 42 = 0; б) 2х2 + 4у2 - 5z = 0.
28. а) -4х2 + 12у2 - 3z2 + 24 = 0; б) 2у2 + 6z2 = 3х.
29. а) 3х2 - 9у2 + z2 + 27 = 0; б) z2 - 2у = -4х2.
30. а) 27х2 - 63у2 + 21z2 = 0; б) 3х2 - 7у2 - 2z2 = 42.
К о н т р о л ь н а я р а б о т а № 2
Дифференцирование и исследование функций
Задание 2.1
Найти
.
1.
.
2.
.
3.
.
4.
.
5.
.
6.
.
7.
.
8.
.
9.
.
10.
.
12.
.
13.
.
14.
.
15.
.
18.
.
22.
27.
28.
29.
30.
Задание 2.2
Найти
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
Задание 2.3
Вычислить предел, пользуясь правилом Лопиталя.
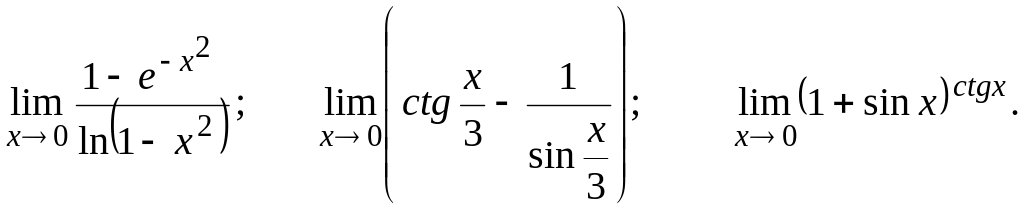
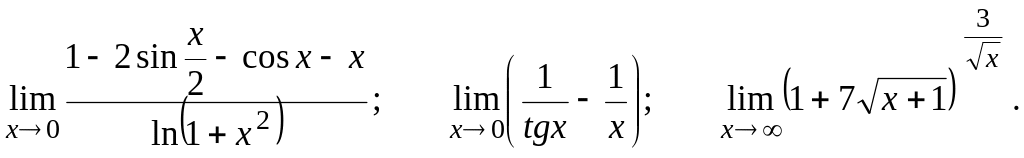
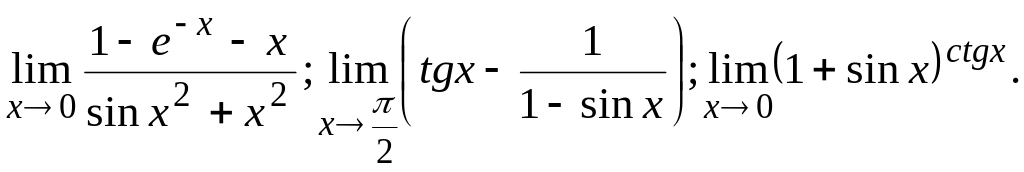
16.
17.
25.
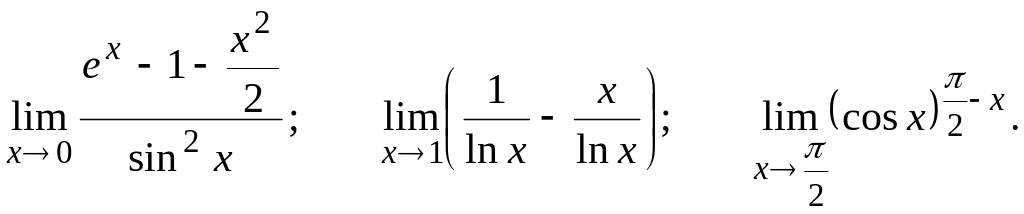
26.
27.
28.
29.
30.
Задание 2.4
Исследовать функцию и построить ее график.
-
1.
10.
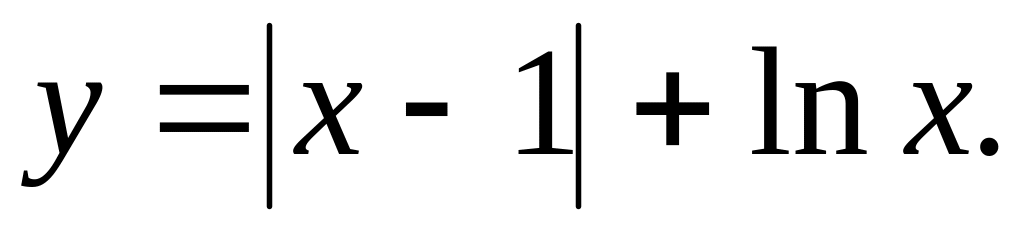
2.
11.
3.
12.
4.
13.
5.
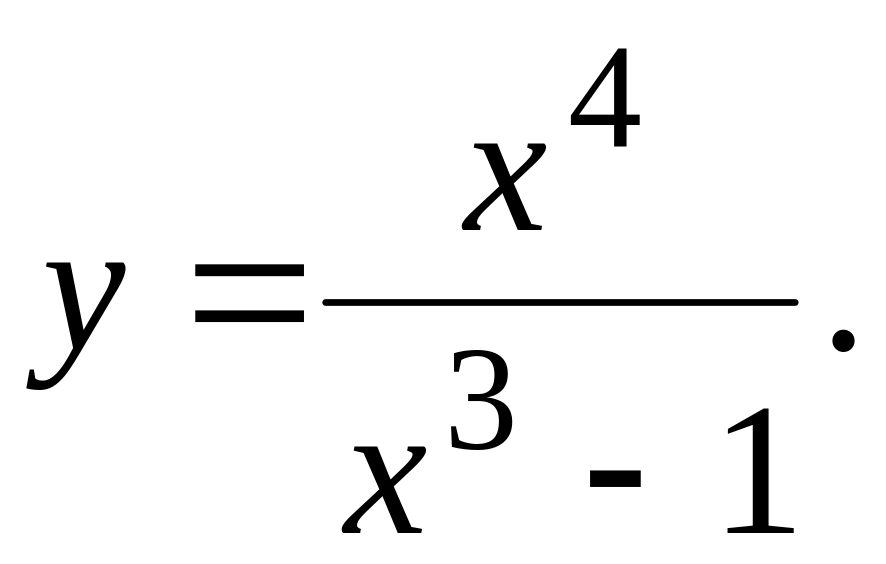
14.
6.
15.
7.
16.
8.
17.
9.
18.
-
19.
25.
20.
26.
21.
27.
22.
28.
23.
29.
24.
30.
К о н т р о л ь н а я р а б о т а № 3
Дифференциальное исчисление функции
нескольких переменных
Задание 3.1
Найти градиент, уравнения касательной плоскости и нормали к заданной поверхности S в точке Мо(Xo,Yo,Zo).
S:
.
S:
.
S:
.
S:
.
S:
.
S:
.
S:
.
S:
.
S:
.
S:
.
S:
.
S:
.
S:
.
S:
.
S:
.
S:
.
S:
.
S:
.
S:
.
S:
.
S:
.
S:
.
S:
.
S:
.
S:
.
S:
.
S:
.
S:
.
S:
.
S:
.
Задание 3.2
Найти наибольшее и наименьшее значения функции Z=Z(X,Y) в области D, ограниченной заданными линиями.
.
z=3x2 + 3y2 - 2x - 2y + 2, D : х = 0, у = 0, х + у – 1 = 0.
Задача 3.3. Найти полные дифференциалы указанных функций:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
Задача
3.4. Найти вторые частные
производные указанных функций. Убедиться
в том, что
.
Задача
3.5. Вычислить значение производной
сложной функции
,
где
,
,
при
с точностью до двух знаков после запятой.
-
,
,
,
.
,
,
,
.
,
,
,
.
,
,
,
.
,
,
,
.
,
,
,
.
,
,
,
.
,
,
,
.
,
,
,
.
,
,
,
.
,
,
,
.
,
,
,
.
,
,
,
.
,
,
,
.
,
,
,
.
,
,
,
.
,
,
,
.
,
,
,
.
,
,
,
.
,
,
,
.
,
,
,
.
,
,
,
.
,
,
,
.
,
,
,
.
,
,
,
.
,
,
,
.
,
,
,
.
,
,
,
.
,
,
,
.
,
,
,
.
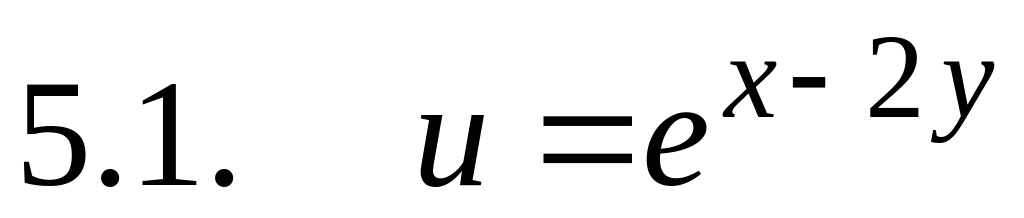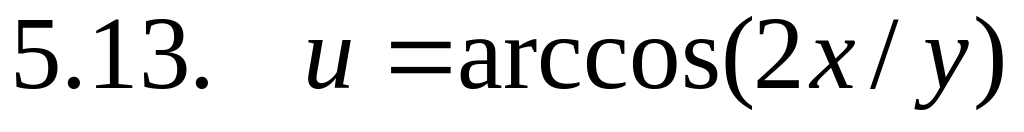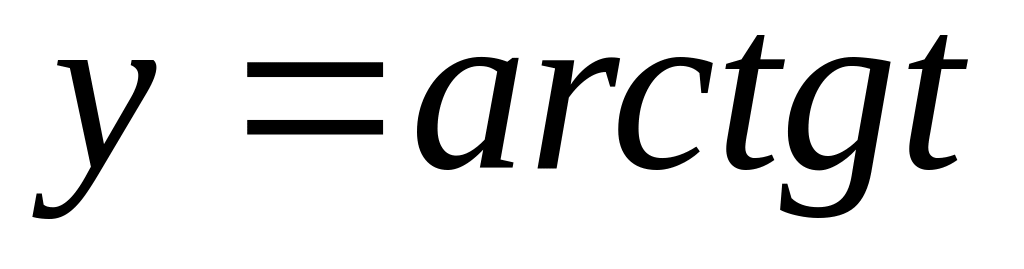КОНТРОЛЬНАЯ РАБОТА № 4.
Интегральное исчисление.
Задача 4.1
С помощью интегрирования по частям вычислить неопределённый интеграл от функции вида
1.
16.
2.
17.
3.
18.
4.
19.
5.
20.
6.
21.
7.
22.
8.
23.
9.
24.
10.
25.
11.
26.
12.
27.
13.
28.
14.
29.
15.
30.
Задача 4.2.
Вычислить неопределённый интеграл с помощью разложения на простейшие дроби подинтегральной функции
1.
16.
2.
17.
3.
18.
4.
19.
5.
20.
6.
21.
7.
22.
8.
23.
9.
24.
10.
25.
11.
26.
12.
27.
13.
28.
14.
29.
15.
30.
Задача 4.3.
Вычислить с помощью подстановки неопределённый интеграл от функции
1.
16.
2.
17.
3.
18.
4.
19.
5.
20.
6.
21.
7.
22.
8.
23.
9.
24.
10.
25.
11.
26.
12.
27.
13.
28.
14.
29.
15.
30.
Задача 4.4.
Вычислить с помощью подстановки неопределённый интеграл от функции
1.
16.
2.
17.
3.
18.
4.
19.
5.
20.
6.
21.
7.
22.
8.
23.
9.
24.
10.
25.
11.
26.
12.
27.
13.
28.
14.
29.
15.
30.
Задача 4.5.
Вычислить площадь фигуры, ограниченной линиями:
Задача 4.6.
Переходя
в полярную систему координат
вычислить с помощью опре-деленного
интеграла площадь, ограниченную кривыми:
первым
витком спирали Архимеда
и отрезком полярной оси
одним
лепестком линии
кардиоидой
и окружностью
12.
одним лепестком линии
13.
четырёхлепестковой розой
14.
лемнискатой Бернулли
первым
и вторым витками спирали Архимеда
и отрезком полярной
оси
окружностью
и прямой
17.
и
(большая часть)
18.
и
(большая
часть)
22.
(меньшая часть)
23.
и
25.
и
26.
(меньшая часть)
27.
(вне окружности)
28.
и первого лепестка линии
29.
между прямыми
Задача 4.7.
Вычислить несобственный интеграл или доказать его сходимость
1.
16.
2.
17.
3.
18.
4.
19.
5.
20.
6.
21.
7.
22.
8.
23.
9.
24.
10.
25.
11.
26.
12.
27.
13.
28.
14.
29.
15.
30.
Задача 4.8.
Вычислить
массу неоднородной пластины
,
ограниченной заданными линиями и имеющей
поверхностную плотность
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 4.9.
Вычислить
с помощью тройного интеграла объем
области
,
ограниченной указанными поверхностями.
№ вар. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 4.10.
Вычислить:
(а)
заряд проводника, располагающегося
вдоль кривой
с плотностью
с помощью криволинейного интеграла
первого рода
(b)
работу силы
вдоль траектории
от точки
до точки
с помощью криволинейного интеграла
второго рода
-
отрезок прямой между
-
дуга параболы
между
-
отрезок прямой между
- четверть окружности
между
-
дуга параболы
между
- дуга параболы
между
-
отрезок прямой между
-
четверть окружности
между
-
дуга параболы
между
-
полуокружность
между
-
дуга параболы
между
-
полуокружность
между
-
дуга параболы
между
- отрезок прямой
между
-
полуокружность
между
-
полуокружность
между
Задача 4.11.
С помощью поверхностного интеграла первого рода
вычислить
расход
жидкости с полем скоростей
протекающей за
единицу времени через часть
плоскости
лежащую в первом октанте. Единичная
нормаль
направлена вне начала координат.
№ вар. |
|
|
|
|
|
|
|
1 |
|
0 |
|
3 |
1 |
2 |
6 |
2 |
0 |
|
|
1 |
1 |
2 |
2 |
3 |
|
|
0 |
2 |
3 |
1 |
8 |
4 |
|
|
|
4 |
1 |
3 |
9 |
5 |
|
0 |
|
1 |
2 |
3 |
6 |
6 |
|
|
0 |
2 |
3 |
1 |
4 |
7 |
|
|
0 |
2 |
1 |
5 |
8 |
8 |
|
|
|
1 |
2 |
4 |
6 |
9 |
0 |
|
|
3 |
4 |
2 |
9 |
10 |
|
|
|
3 |
2 |
1 |
6 |
11 |
|
|
0 |
2 |
1 |
3 |
8 |
12 |
|
|
0 |
1 |
3 |
2 |
6 |
13 |
|
|
1 |
4 |
1 |
2 |
8 |
14 |
5 |
|
|
2 |
4 |
1 |
8 |
15 |
|
0 |
|
1 |
4 |
2 |
6 |
16 |
|
|
5 |
5 |
3 |
1 |
10 |
17 |
|
|
3 |
3 |
5 |
1 |
10 |
18 |
|
|
0 |
3 |
1 |
2 |
6 |
19 |
|
|
4 |
2 |
1 |
1 |
4 |
20 |
0 |
|
|
1 |
2 |
4 |
6 |
21 |
|
0 |
|
1 |
3 |
2 |
6 |
22 |
|
|
4 |
2 |
3 |
1 |
6 |
23 |
|
4 |
|
2 |
3 |
4 |
9 |
24 |
|
|
0 |
4 |
2 |
1 |
8 |
25 |
|
|
-8 |
3 |
1 |
5 |
10 |
26 |
|
|
|
3 |
4 |
1 |
8 |
27 |
|
|
|
1 |
4 |
3 |
12 |
28 |
|
|
|
3 |
4 |
2 |
8 |
29 |
|
0 |
|
2 |
4 |
3 |
10 |
30 |
7 |
|
|
4 |
3 |
2 |
9 |
