11. Основная теорема алгебры (без док-ва).

Теорема: Всякий многочлен, степень которого не меньше 1, имеет хотя бы один корень, в общем случае комплексный.

Пример: 59 (Метод Гаусса)

12. Формулы Виета.

Формулы Виета — формулы, выражающие коэффициенты многочлена через его корни. Этими формулами удобно пользоваться для проверки правильности нахождения корней многочлена, а также для составления многочлена по заданным его корням.

Если α₁, α₂, … , α_n — корни многочлена xⁿ + a₁x^n-1 + a₂x^n-2 + …+ a_n (каждый корень взят соответствующее его кратности число раз), то коэффициенты выражаются в виде симметрических многочленов от корней, а именно:

a₁ = - (α₁ + α₂ + … + α_n) a₂ = α₁α₂ + α₁α₃ + … + α₁α_n + α₂α₃ + … + α_n-1α_n

a₃ = - (α₁α₂α₃ + α₁α₂α₄ + … + α_n-2α_n-1a_n) …

a_n-1 = (-1)^n-1 (α₁α₂ … α_n-1 + α₁α₂ … α_n-2α_n + α_n-2α_n-1…α_n) a_n = (-1)ⁿ α₁α₂…α_n

Иначе говоря (−1)^ka_k равно сумме всех возможных произведений из k корней.

Если старший коэффициент многочлена a₀ ≠ 1, то для применения формулы Виета необходимо предварительно разделить все коэффициенты на a₀ (это не влияет на значение корней многочлена). В этом случае формулы Виета дают выражение для отношений всех коэффициентов к старшему. Из последней формулы Виета следует, что если корни многочлена целочисленные, то они являются делителями его свободного члена, который также целочисленен.

Доказательство осуществляется рассмотрением равенства: xⁿ + a₁x^n-1 + a₂x^n-2 + …+ a_n = (x – a₁)(x – a₂) … (x - a_n)

Квадратное уравнение: Сумма корней приведенного квадратного уравнения равна второму коэффициенту с обратным знаком, а произведение корней равно свободному члену.

Если x₁ и x₂ — корни квадратного уравнения ax² + bx + c = 0 , то x₁ + x₂ = -b/a и x₁x₂ = c/a .

В частном случае, если a = 1 (приведенная форма x² + px + q = 0), то x₁ + x₂ = − p и x₁x₂ = q.

Кубическое уравнение: Если x₁,x₂,x₃ - корни кубического уравнения p(x) = ax³ + bx² + cx + d = 0,

то x₁ + x₂ +x₃ = -b/a, (x₁x₂ + x₁x₃ + x₂x₃) = c/a, x₁x₂x₃ = -d/a

Тема 2. Теория определителей

13. Определители второго и третьего порядка.

Числа m и n называются размерностями матрицы.

Матрица называется квадратной, если m = n. Число n в этом случае называют порядком квадратной матрицы.

Каждой квадратной матрице можно поставить в соответствие число, определяемое единственным образом с использованием всех элементов матрицы. Это число называется определителем.

Определителем второго порядка называется число, полученное с помощью элементов квадратной матрицы 2-го порядка следующим образом: .

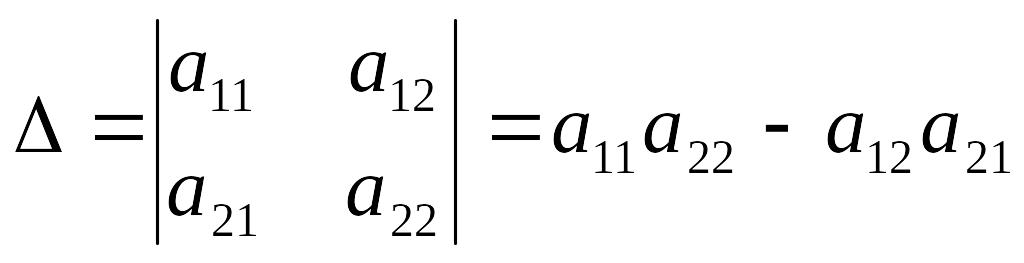При этом из произведения элементов, стоящих на так называемой главной диагонали матрицы (идущей из левого верхнего в правый нижний угол) вычитается произведение элементов, находящихся на второй, или побочной, диагонали.

Определителем третьего порядка называется число, определяемое с помощью элементов квадратной матрицы 3-го порядка следующим образом:

З амечание. Для того чтобы легче запомнить эту формулу, можно использовать так называемое правило Крамера (треугольников). Оно заключается в следующем: элементы, произведения которых входят в определитель со знаком «+», располагаются так:

образуя два треугольника, симметричных относительно главной диагонали. Элементы, произведения которых входят в определитель со знаком «-», располагаются аналогичным образом относительно побочной диагонали: