2.3. Классическая линейная множественная регрессия

Наиболее простыми моделями множественной регрессии, как и в случае парной регрессии, являются линейные модели:

, (2.4)

где ₀, ₁, …, _m – параметры, которые в данном случае имеют достаточно простую интерпретацию. Параметр ₀ определяет значение зависимой переменной при отсутствии какого-либо влияния на нее, а параметры ₁, …, _m – степень влияния соответствующих факторов.

Для классической линейной регрессионной модели требуется выполнение шести условий:

1. равенство нулю математического ожидания случайной компоненты,

2. постоянство дисперсии случайной компоненты (свойство гомоскедастичности),

3. взаимная независимость случайных остатков, относящихся к разным наблюдениям (отсутствие автокорреляции),

4. независимость случайных отклонений от объясняющих переменных,

5. отсутствие сильной линейной зависимости между объясняющими переменными (отсутствие мультиколлинеарности),

6. нормальность распределения случайных остатков _i.

Первая задача состоит в оценке параметров модели (2.4) по имеющимся наблюдениям. Если модель удовлетворяет выше приведенным условиям, то оценивание параметров может быть проведено классическим методом наименьших квадратов (МНК).

Введем следующие обозначения:

• вектор-столбец значений зависимой переменной

• матрица значений объясняющих переменных

• вектор параметров уравнения регрессии и вектор случайных ошибок

В матричном виде уравнение множественной регрессии относительно имеющегося массива наблюдений выглядит следующим образом:

(2.5)

Применение МНК предполагает решение следующей оптимизационной задачи:

или в матричном виде:

Раскрывая скобки в данном выражении, получим:

.

Поскольку есть число, то оно совпадает со своим транспонированным выражением . Таким образом, критерий оптимальности МНК можно записать в виде:

Продифференцируем данное выражение по вектору параметров А и приравняем производную к нулю (нулевой матрице):

, т.е.

(2.6)

Разрешая данное уравнение относительно А, получим матричную формулу для оценок параметров:

(2.7)

Заметим, что для применения МНК к оценке параметром уравнения множественной регрессии, необходимо, чтобы матрица X^TX была невырожденной, т.е. чтобы ее определитель был отличен от нуля.

Пример 2.1.

Изучается выпуск продукции некоторой отраслью промышленности путем определения производственной функции вида: , где y – выпуск, x₁ - затраты труда, x₂ - затраты капитала. Определим параметры данного уравнения, используя следующие данные.

x1	118	102	116	124	114	154	115	98
x2	105	50	54	42	36	106	88	46
y	203	88	110	56	80	237	160	75

Матрица значений объясняющих переменных, вектор значений результирующей переменной и вектор параметров имеют вид:

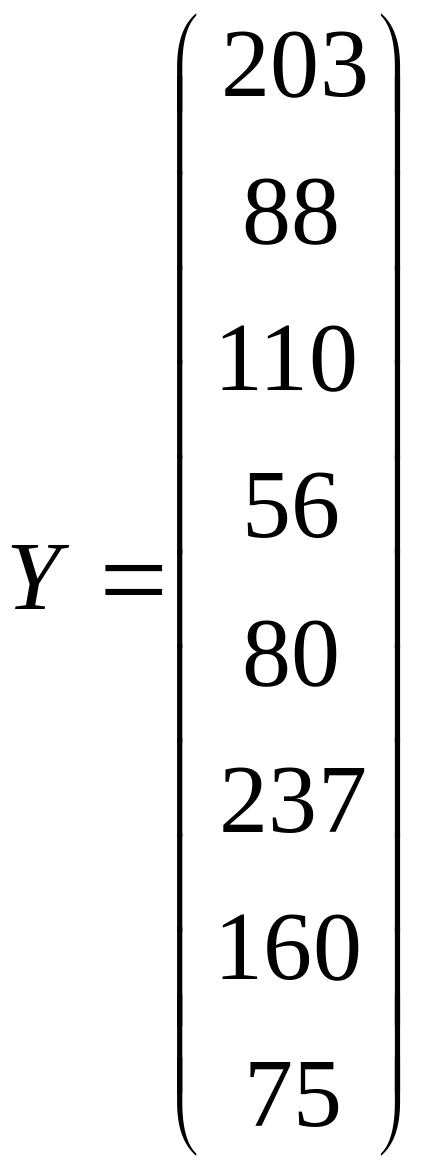
Определим параметры регрессионной модели с помощью уравнения (2.7). Для этого рассчитаем следующие матрицы:

, ,

,

Таким образом, регрессионное уравнение имеет вид:

.

Можно предложить другой способ определения коэффициентов. Записывая в развернутом виде матричное уравнение (2.6), можно получить следующую систему линейных нормальных уравнений для определения коэффициентов уравнения регрессии:

(2.8)

Решая данную систему, например, методом Крамера можно определить оценки коэффициентов, которые, естественно, будут совпадать со значениями, получаемыми с помощью формулы (2.7).

При большом числе наблюдений нахождение оценок параметров «вручную» весьма трудоемко. Как и в случае парной регрессии, здесь удобнее воспользоваться программными средствами, например, уже упоминавшейся функцией ЛИНЕЙН в ППП Excel (параграф 1.5).

В отличие от случая парной регрессии здесь в п. 2 выделяется область не 5х2, а (m+1)x2, в п.5 в окно Известные значения_х вводится массив заданных значений всех объясняющих переменных x₁, x₂,…, x_m. Наконец, заполнение выделенной зоны происходит по следующей схеме:

			…
			…
R2		#Н/Д	…	#Н/Д
F-статистика	n-m-1	#Н/Д	…	#Н/Д
QR	Qe	#Н/Д	…	#Н/Д

Таким образом, дополнительная информация касается только оценок параметров регрессии и их стандартных ошибок.