4 При освещении тонкой плёнки можно наблюдать интерферен­цию световых волн, отражённых от верхней и нижней поверхности плёнок. Для белого света, представляющего собой смешение электромагнитных волн из всего оптического спектра интерференционные полосы приобретают окраску. Это явление получило название цветов тонких плёнок. Цвета тонких плёнок наблюдаются на стенках мыльных пузырьков, на плёнках масла, нефти, на поверхности металлов при их закалке (цвета побежалости).

Для объяснения этих явлений рассмотрим расположенную в вакууме плоско параллельную диэлектрическую пластинку (рис.) толщины   с показателем преломления  , где   - диэлектрическая проницаемость диэлектрика, освещаемую плоской световой монохроматической волной с длиной волны   под углом   (рис. 4.16). При отражении световых волн от верхней и нижней поверхности пластинки между отражёнными волнами возникнет оптическая разность хода   , которая является следствием того факта, что волна, отражённая от нижней поверхности пластинки проходит больший путь внутри диэлектрической пластинки, чем волна, отражённая от верней поверхности в вакууме, приобретающая дополнительный набег фазы  при отражении от оптически более плотной среды

ПОЛОСЫ РАВНОГО НАКЛОНА       

система чередующихся светлых и тёмных полос, наблюдаемая на экране при освещении прозрачного слоя п о с т о я н н о й т о л щ и н ы (плоскопараллельной пластинки) непараллельным пучком монохроматич. излучения. Каждая полоса создаётся лучами света S и S1 (рис.), падающими на поверхность слоя под одним и тем же углом (р. Появление П. р. н. обусловлено интерференцией света, отражённого «т передней и задней границы пластинки. П. р. н. локализованы в бесконечности и для их наблюдения интерферирующие лучи собирают с помощью линзы L на экран Э или фотопластинку.

Схема наблюдения полос равного наклона. Лучи S и S1, падающие под одним углом, собираются линзой в одной точке О. Лучи, падающие под др. углом (напр., S'), собираются линзой в др. точке О'

1 Интерференция света — нелинейное сложение интенсивностей двух или нескольких световых волн. Это явление сопровождается чередующимися в пространстве максимумами и минимумами интенсивности. Её распределение называется интерференционной картиной. При интерференции света происходит перераспределение энергии в пространстве. Пусть две волны одинаковой частоты, накладываются друг на друга, возбуждают в некоторой точке пространства колебания одинакового направления : Амплитуда результирующего колебания в данной точке определяется формулой Если разность фаз , возбуждаемых волнами колебаний станет постоянной, то волны называются когерентными. Источники таких волн называются когерентными.

Опыт Юнга  Как было уже показано, для наблюдения интерференции света необходимо иметь когерентные световые пучки, для чего применяются различные приёмы. В опыте Юнга когерентные пучки получали разделением и последующим сведением световых лучей, исходящих из одного и того же источника (метод деления волнового фронта). Свет от источника S, прошедший через узкую щель в экране А, падет на экран В с двумя щелями S₁ и S₂, расположенными достаточно близко друг к другу на расстоянии d. Эти щели являются когерентными источниками света. Интерференция наблюдается в области, в которой перекрываются волны от этих источников (поле интерференции). На экране Э мы видим чередование полос с максимумом и минимумом интенсивности света.

      Экран расположен на расстоянии l от щелей, причем   Рассмотрим две световые волны, исходящие из точечных источников S₁ и S₂. Показатель преломления среды-n  Вычислим ширину полос интерференции (темных и светлых полос). Интенсивность в произвольной точке P экрана, лежащей на расстоянии x от О, определяется (для вакуума, когда n = 1) оптической разностью хода   . Из рис. 8.1 имеем  ;       ,      отсюда   , или  .  Из условия    следует, что   , поэтому

      Отсюда получим, что максимумы интенсивности будут наблюдаться в случае, если      (m = 0, 1, 2, …)

      а минимумы – в случае, если

      Расстояние между двумя соседними максимумами (или минимумами) равно:       и не зависит от порядка интерференции (величины m) и является постоянной для данных l, d.      Расстояние между двумя соседними максимумами называется расстоянием между интерференционными полосами, а расстояние между соседними минимумами – шириной интерференционной полосы.      Т.к.    обратно пропорционально d, при большом расстоянии между источниками, например при   , отдельные полосы становятся неразличимыми, сравнимыми с длиной волны   . Поэтому необходимо выполнять условие   .      Этот опыт показывает, что интерференционная картина, создаваемая на экране  двумя когерентными источниками света, представляет собой чередование светлых и темных полос. Главный максимум, соответствующий   , проходит через точку О. Вверх и вниз от него располагаются максимумы (минимумы) первого (   ), второго (   ) порядков и т. д.      Из перечисленных формул видно, что ширина интерференционной полосы и расстояние между ними зависят от длины волны λ. Только в центре картины при    совпадут максимумы всех волн. По мере удаления от центра максимумы разных цветов смещаются друг относительно друга все больше и больше. Это приводит, при наблюдении в белом свете, ко все большему размытию интерференционных полос. Интерференционная картина будет окрашенной, но нечеткой (смазанной).      Измерив   , зная l и d, можно вычислить длину волны λ. Именно так  вычисляют длины волн разных цветов в спектроскопии.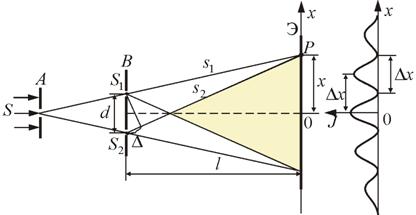

3 Зеркала Френеля. Френель предложил в качестве двух когерентных источников воспользоваться двумя изображениями одного и того же действительного источника света в двух плоских зеркалах. где A₁O и А₂O − два плоских зеркала, расположенных под углом φ; S − источник света, находящийся на расстоянии r от места соприкосновения зеркал в точке О. Для построения изображений источника S в обоих зеркалах воспользуемся тем, что мнимое изображение, даваемое плоским зеркалом, лежит за зеркалом на таком же расстоянии, на каком объект лежит перед зеркалом. Проведем из точки О окружность с радиусом r = OS и опустим из точки S перпендикуляр на продолжение прямой ОА₁; точка пересечения продолжения этого перпендикуляра с окружностью В₁ даст изображение источника S в первом зеркале ОА₁. Так же построим изображение В₂ даваемое во втором зеркале ОA₂. С другой стороны, изображение B₂ лежит в той точке, куда переместилось бы изображение В₁ при повороте первого зеркала ОА₁ на угол φ.Поэтому <B1OB2 = 2φ, и линейное расстояние d между В₁ и В₂ приближенно равно 2φr d = 2φr. (1) Свет от обоих изображений В₁ и В₂ падает на экран DD^/, отстоящий от зеркал на расстоянии L_o. Заслонка Е мешает попадать на экран DD^/ прямому свету от источника S. Так как оба изображения B₁ и В₂ воспроизводят колебания одного и того же действительного источника, то они когерентны, и на экране DD^/ наблюдаются интерференционные полосы. Расстояние между полосами Δl равно Δl = λL/d,где L − расстояние от источников до места наблюдения полос.Подставляя сюда вместо d его значение по (1) и замечая, что приближенно L = L_o + r, получим Δl = (L_o + r)λ/(2φr), или отсюда λ = 2φr•Δl/(L_o + r).  Так как в последней формуле все величины, стоящие в правой части, доступны измерению, то из нее видно, что опыт с зеркалами Френеля позволяет измерить длину световых волн λ.  Зеркала в опыте Френеля приходится располагать под весьма малым углом φ друг к другу, так как иначе полосы получаются слишком узкими. Источник света берется в виде узкой щели, параллельной ребру О, образованному зеркалами. При этом интерференционные максимумы имеют вид прямых параллельных полос. При наблюдении в белом свете центральная полоса получается белая (k = 0, усиливаются лучи всех длин волн λ), остальные − окрашенные.

Бипризма Френеля. Этот опыт представляет собою простой вариант с бизеркалами Френеля. Свет от источника S преломляется в двух призмах с малыми преломляющими углами A и A^/ (рисунок), сложенных основаниями. Призмы отклоняют лучи в противоположных направлениях и, таким образом, возникают два мнимых когерентных источника света S^/ и S^//. Лучи от этих источников, перекрываясь в области D, дают интерференционные полосы.

Зеркало Ллойда. В опыте, предложенном Ллойдом, интерферируют лучи, исходящие непосредственно от источника S (рисунок) и отраженные от поверхности зеркала АВ. Лучи, отраженные от зеркала АВ, как бы исходят от мнимого источника S₁ когерентного с S. Для того чтобы расстояние d между S и S^/ было достаточно мало, лучи должны отражаться от зеркала под углом, близким к 90°. Источником света служит щель, параллельная плоскости зеркала. Особенность интерференционной картины, наблюдаемой с помощью зеркала Ллойда, заключается в том, что центральная полоса получается не светлой, а темной. Это указывает на то, что лучи, проходящие одинаковые геометрические пути, все же сходятся в опыте Ллойда с разностью хода λ/2. Такая „потеря" полуволны (или, другими словами, изменение фазы на π) происходит при отражении света от поверхности стекла, коэффициент преломления которого больше, чем воздуха. В дальнейшем мы увидим, в каких случаях при отражении света от прозрачной среды происходит потеря полуволны.

Опыт Линника. Во всех описанных выше опытах по интерференции два когерентных источника расположены на прямой, перпендикулярной к среднему направлению распространения света. Опыт, в котором когерентные источники S и S^/ расположены на самой прямой, вдоль которой распространяется свет, был впервые предложен в 1935 г. советским физиком В. П. Линником. Схема опыта Линника такова: свет от точечного источника S (рисунок) дает сферическую волну АВ. На пути волны АВ расположена плоскопараллельная полупрозрачная пластинка, которая несколько ослабляет волну АВ, не искажая ее поверхности. В пластинке делается малое отверстие S^/. По принципу Гюйгенса оно служит источником новой сферической волны А^/В^/ с центром в S^/. Волны  АВ  и  A^/B ^/ когерентны и дают на экране D интерференционные полосы в виде колец.  Источник S может быть также взят в виде узкой полоски (освещенная в непрозрачном экране щель) и отверстие S^/ − в виде параллельной ему щели. Тогда интерференционные полосы на экране D имеют вид прямых линий. 

5 Интерференция на клине Две поверхности, расположение под малым углом α, образуют систему получившую название клин. Клин имеет разную толщину, а поэтому при освещении поверхности клина монохроматическим светом на поверхности клина будут наблюдаться интерференционные максимумы и минимумы (смотри интерференцию на плёнке), т.к. в одних точках поверхности толщина клина соответствует условию наблюдению максимума, а в других – условию минимума. Определим ширину интерференционной полосы.Пусть в точке А поверхности клина возникает максимум m-ого порядка. Толщина клина - d_m+1. В точке В возникает максимум (m+1)-го порядка. Толщина плёнки в этом месте - d_m+1. Условие наблюдения максимума при толщине d_m и d_m+1: 2d_mn=(2m+1)λ/2; 2d_m+1n=(2m+3) λ/2.

Вычтем из второго уравнения первое:

. d_m+1-d_m – разность толщины клина в местах наблюдения m-ого и (m+1)-го максимумов. На рисунке 3. Из прямоугольника: AB=Δy=BD/sinα, Δy – ширина интерференционной полосы .Если угол при вершине мал, то  , , α[рад].

Ширина интерференционного минимума или расстояния между соседними минимумами равна ширине интерференционного максимума.

Кольца Ньютона. Частым случаем полос равной толщины являются кольца Ньютона, которые наблюдаются в схеме, изображённой на рисунке 4. Плосковыпуклая линза с большим радиусом кривизны R выпуклой поверхностью лежит на плоской пластине и соприкасается с ней в точке О. Параллельный пучок света падает нормально на плоскую поверхность промежутка между линзой и пластиной. При наложении отраженных волн возникают интерференционные полосы равной толщины, имеющие вид колец. Вид этих колец в случае монохроматического света показан на рисунке 5. В центре наблюдается минимум нулевого порядка (тёмное пятно). Центральный минимум окружён системой чередующихся окрашенных и тёмных колец, ширина и интенсивность которых постоянно убывает по мере удаления от центрального пятна. Расчёт радиусом окрашенных и тёмных колец. На рисунке 6 изображены интерферирующие волны, распространяются вдоль лучей 1 и 2. Разность хода волн равна: , где d – толщина зазора между линзой и пластиной, где наблюдается интерференция, n – показатель преломления прослойки, λ/2 – потеря полволны при отражении 1-ой волны от стеклянной пластинки (при условии n<n_стекла). Для наблюдения максимума интерференции или окрашенного кольца: , где m-ого порядка окрашенного кольца (m=1,2,3…). Значит, . Для минимума интерференции  , или  . Радиус кольца определим, используя геометрию рисунка 4 OD=d. Из треугольника AO₁D: . Пренебрегая d², получим:  . Если подставим значения d, соответствующее минимуму интерференции, получим выражение для радиуса окрашенного кольца m-ого порядка.

Если между линзой и пластинкой воздушная прослойка, то n=1.

6 Принцип гюйгенса - френеля

Дифракцией называется огибание волнами препятствий, встречающихся на их пути, или в более широком смысле - любое отклонение распространения волн вблизи препятствий от законов геометрической оптики. Благодаря дифракции волны могут попадать в область геометрической тени, огибать препятствия, проникать через небольшие отверстия в экранах и т. д. Например, звук хорошо слышен за углом дома, т. е. звуковая волна его огибает. Явление дифракции объясняется с помощью принципа Гюйгенса (см. § 170), согласно которому каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн задает положение волнового фронта в следующий момент времени. Пусть плоская волна нормально падает на отверстие в непрозрачном экране (рис. 256). Согласно Гюйгенсу, каждая точка выделяемого отверстием участка волнового фронта служит источником вторичных волн (в однородной изотропной среде они сферические). Построив огибающую вторичных волн для некоторого момента времени, видим, что фронт волны заходит в область геометрической тени, т. е. волна огибает края отверстия. Явление дифракции характерно для волновых процессов. Поэтому если свет является волновым процессом, то для него должна наблюдаться дифракция, т. е. световая волна, падающая на границу какого-либо непрозрачного тела, должна огибать его (проникать в область геометрической тени). Из опыта, однако, известно, что предметы, освещаемые светом, идущим от точечного источника, дают резкую тень и, следовательно, лучи не отклоняются от их прямолинейного распространения. Почему же возникает резкая тень, если свет имеет волновую природу? К сожалению, теория Гюйгенса ответить на этот вопрос не могла. Принцип Гюйгенса решает лишь задачу о направлении распространения волнового фронта, но не затрагивает вопроса об амплитуде, а следовательно, и об интенсивности волн, распространяющихся по разным направлениям. Френель вложил в принцип Гюйгенса физический смысл, дополнив его идеей интерференции вторичных волн. Согласно принципу Гюйгенса - Френеля, световая волна, возбуждаемая каким-либо источником S, может быть представлена как результат суперпозиции когерентных вторичных волн, «излучаемых» фиктивными источниками. Такими источниками могут служить бесконечно малые элементы любой замкнутой поверхности, охватывающей источник S. Обычно в качестве этой поверхности выбирают одну из волновых поверхностей, поэтому все фиктивные источники действуют синфазно. Таким образом, волны, распространяющиеся от источника, являются результатом интерференции всех когерентных вторичных волн. Френель исключил возможность возникновения обратных вторичных волн и предположил, что если между источником и точкой наблюдения находится непрозрачный экран с отверстием, то на поверхности экрана амплитуда вторичных волн равна нулю, а в отверстии - такая же, как при отсутствии экрана. Учет амплитуд и фаз вторичных волн позволяет в каждом конкретном случае найти амплитуду (интенсивность) результирующей волны в любой точке пространства, т. е. определить закономерности распространения света. В общем случае расчет интерференции вторичных волн довольно сложный и громоздкий, однако, как будет показано ниже, для некоторых случаев нахождение амплитуды результирующего колебания осуществляется алгебраическим суммированием.

Зоны Френеля

        участки, на которые можно разбить поверхность световой (или звуковой) волны для вычисления результатов дифракции света (См. Дифракция света) (или звука). Впервые этот метод применил О. Френель в 1815—19. Суть метода такова. Пусть от светящейся точки Q (рис.) распространяется сферическая волна и требуется определить характеристики волнового процесса, вызванного ею в точке Р. Разделим поверхность волны S на кольцевые зоны; для этого проведём из точки Р сферы радиусами PO, Pa = PO + ^λ/₂; Pb = Pa + ^λ/₂, Pc = Pb + ^λ/₂, (О — точка пересечения поверхности волны с линией PQ; λ — длина световой волны). Кольцеобразные участки поверхности волны, «вырезаемые» из неё этими сферами, и называется З. Ф. Волновой процесс в точке Р можно рассматривать как результат сложения колебаний, вызываемых в этой точке каждой З. Ф. в отдельности. Амплитуда таких колебаний медленно убывает с возрастанием номера зоны (отсчитываемого от точки О), а фазы колебаний, вызываемых в Р смежными зонами, противоположны. Поэтому волны, приходящие в Р от двух смежных зон, гасят друг друга, а действие зон, следующих через одну, складывается. Если волна распространяется, не встречая препятствий, то, как показывает расчёт, её действие (сумма воздействий всех З. Ф.) эквивалентно действию половины первой зоны. Если же при помощи экрана с прозрачными концентрическими участками выделить части волны, соответствующие, например, N нечётным зонам Френеля, то действие всех выделенных зон сложится и амплитуда колебаний U_нечёт в точке Р возрастёт в 2N раз, а интенсивность света в 4N² раз, причём освещённость в точках, окружающих Р, уменьшится. То же получится при выделении только чётных зон, но фаза суммарной волны U_чёт будет иметь противоположный знак.

         Такие зонные экраны (т. н. линзы Френеля) находят применение не только в оптике, но и в акустике и радиотехнике — в области достаточно малых длин волн, когда размеры линз получаются не слишком большими (сантиметровые радиоволны, ультразвуковые волны).

         Метод З. Ф. позволяет быстро и наглядно составлять качественное, а иногда и довольно точное количественное представление о результате дифракции волн при различных сложных условиях их распространения. Он применяется поэтому не только в оптике, но и при изучении распространения радио- и звуковых волн для определения эффективной трассы «луча», идущего от передатчика к приёмнику; для выяснения того, будут ли при данных условиях играть роль дифракционные явления; для ориентировки в вопросах о направленности излучения, фокусировке волн и т.п

7 Пятно ПуассонаС помощью спирали Френеля можно получить еще один замечательный результат. Действительно, если на пути сферической волны находится непрозрачное круглое отверстие (любого размера), то оказывается закрытым какое-то число внутренних зон Френеля. Но вклад в колебания в точке наблюдения, находящегося в центре геометрической тени, будут давать остальные зоны. В результате в этой точке должен наблюдаться свет. Этот результат показался в свое время Пуассону столь невероятным, что он выдвинул его как возражение против рассуждений и расчетов Френеля при рассмотрении дифракции. Однако, когда был проведен соответствующий опыт, такое светлое пятнышко в центра геометрической тени было обнаружено. С тех пор оно носит название пятна Пуассона, хотя он не допускал и самой возможности его существования.

Д ифракция на круглом отверстии В плане историческом теоретическое исследование явлений дифракции было исключительно важным для утверждения представлений о волновой природе света. Что и говорить, правильные представления в каждой области очень важны для общего правильного представления о Природе. Только в таком случае мы можем успешно использовать явления всякого рода для наших нужд. В оптике различные приборы по понятным причинам имеют круглые входные отверстия, диафрагмы и проч. И неизбежная дифракция на круглых отверстиях ограничивает возможности этих приборов. При знакомстве, например, с линзой мы ограничивались параксиальными лучами, достаточно узкими пучками света. Лишь при этом условии преломляющие поверхности линзы можно изготавливать сферическими. Но это, естественно, ограничивает возможности изготовленных из таких линз оптических приборов и, в частности, из-за дифракции. А вот, например, для астрономических наблюдений необходимы грандиозно большие входные отверстия, изменяемые метрами. В этом случае задача изготовления телескопа неимоверно усложняется, телескопы с такими отверстиями очень дороги и, соответственно, уникальны. Вот для некоторого, хотя бы, понимания этих проблем нам и необходимо заняться обсуждением дифракции на круглых отверстиях.

8 Рассмотрим схему наблюдения дифракции Фраунгофера, представленную на рис.3. Плоская монохроматическая волна падает нормально на плоскость Щ, где расположена бесконечно длинная щель шириной b (щель можно считать бесконечно длинной, если ее длина намного больше ее ширины. Так при ширине в 0,01 - 0,05 мм длина в несколько миллиметров может считаться бесконечной). За щелью расположена линза Л, в фокальной плоскости которой находится экран Э. Наличие линзы равносильно тому, что экран расположен как бы на "бесконечном" расстоянии от объекта. Если бы свет распространялся прямолинейно в соответствии с законами геометрической оптики, то в фокальной плоскости линзы получилась бы бесконечно узкая светлая полоса, проходящая через точку N₀ на экране Э. Но в соответствии с принципом Гюйгенса-Френеля каждая точка волнового фронта, достигающего плоскости, где расположена щель, является источником вторичных волн. Тогда лучи, идущие от всех этих вторичных источников под некоторым углом j к первоначальному направлению, образуют плоский волновой фронт и соберутся в фокальной плоскости линзы в т.N_j (рис.3).

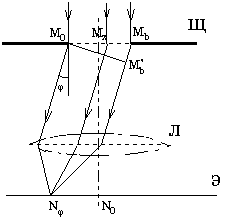
Рис.3. Дифракция Фраунгофера на одной щели.

Расчет поля в плоскости экрана проведём непосредственно на основе принципа Гюйгенса-Френеля, не используя формулу (1). Для этого разобъем открытую часть поверхности щели на зоны в виде узких полосок одинаковой ширины dх, параллельных краям щели. Эти элементарные участки становятся источниками вторичных волн. Амплитуды dA0 этих волн, приходящих в т. Nj на экране от разных полосок, одинаковы, так как все зоны имеют одинаковую площадь и одинаковый к направлению вторичных волн угол j. Эти амплитуды будут пропорциональны произведению амплитуды падающей волны Е0 на размер полоски dx, т.е. dA0 = CE0 dx (2) где С - коэффициент пропорциональности. Однако фазы колебаний, приходящих от различных участков щели, будут различаться. Для определения разности фаз проведем прямую М0Мb', перпендикулярную к направлению дифрагированных лучей, и найдем разность хода, возникающую на пути от прямой М0Мb до прямой М0Мb'. Из рис.3 видно, что разность хода между волнами, идущими от точки М0 и от точки Мх, расположенной на расстоянии х от т.М0, равна хSinj. Следовательно, если считать, что фаза волны, приходящей в т. Nj из т.М0, равна нулю, то колебание dUj, приходящее от элемента dх из окрестности точки Мх в т. Nj, может быть записано в виде: dUj = dА0 cos(wt-kxSinj) где k=2p/l - волновое число, w - частота колебания. Для вычисления величины Uj в т. Nj необходимо просуммировать вклады от различных участков щели, т.е. проинтегрировать dUj в пределах от х = 0 до х = b:

(3)

Сомножитель cos(wt-1/2kbsinj) в формуле (3) описывает временное изменение поля в точке наблюдения с частотой w, а модуль выражения, стоящего перед косинусом, есть амплитуда Aj результирующей волны в точке Nj :       (4)

Отметим, что амплитуда волны, распространяющейся в направлении j=0, пропорциональна ширине щели b и равна A0=CE0b (5) и выражение (4) можно переписать в виде       (4')

Интенсивность света определяется квадратом амплитуды, т.е.

(6)

где I₀ - интенсивность в центре дифракционной картины, u =1/2 kbSinj.

Рис.4. Дифракция Фраунгофера на одной щели: распределение интенсивности на экране в зависимости от синуса угла дифракции.

На рис.4 приведен график зависимости интенсивности Ij от синуса угла дифракции j. Интенсивность максимальна для направления j_0max=0, совпадающего с направлением распространения падающей волны. Направления, соответствующие последующим максимумам, можно найти из решения задачи поиска экстремума функции (6). Эти направления примерно соответствуют значениям u, равным u_1max= 1.43p@3p/2, u_2max= 2.46p@5p/2, u_3max= 3.47p@ 7p/2,... Соотношения интенсивностей главного и последующего максимумов равны I_0max = I_1max = I_2max = I_3max =... = 1 : 0,045 : 0, 016 : 0,008:. и не зависят ни от ширины щели, ни от длины волны. В то же время для направлений Sinj = l/b, 2l/b, 3l/b, 4l/b... , удовлетворяющих уравнению Sin u = 0, интенсивность равна нулю. Эти направления соответствуют случаю, когда разность хода между волнами, приходящими от крайних участков щели, равна целому числу длин волн. Это означает, что для любого произвольно выбранного участка щели всегда найдется другой, равный по величине, участок, излучение от которого придет строго в противофазе с излучением от выбранного участка. Тем самым, в результате интерференции интенсивность распространяющегося в этих направлениях излучения будет равна нулю. Из рис.4 видно, что основная часть светового потока сосредоточена в центральной дифракционной полосе, определяемой значениями Sinj =l/b (так называемый центральный максимум), малая его часть будет распространяться в пределах первых (около 5%) и вторых (около 2%) максимумов и т.д.

Рис.5. Дифракция Фраунгофера на одной щели: 1 - узкая щель, 2 - широкая щель.

Рассмотрим влияние ширины щели на распределение интенсивности дифракционной картины (рис.5). Увеличение ширины щели приводит к приближению первых минимумов к центру дифракционной картины, при этом резкость дифракционного максимума увеличивается (рис.5, кривая 2). Соотношение интенсивностей света в отдельных максимумах не изменяется, однако увеличивается абсолютное значение интенсивности, связанное с тем, что с увеличением ширины щели увеличивается энергия проходящего через нее излучения. В заключении отметим, что дифракция Фраунгофера может наблюдаться и при падении сферической волны на объект, и при отсутствии линзы. Из формулы (1) можно показать, что условия для наблюдения дифракции Фраунгофера имеют вид: b²/lr <<1, b²/ls <<1.

9 КОРНЮ СПИРАЛЬ (по имени М. А. Корню, М. А. Соrnu) (клотоида) - кривая, используемая для графич. вычисления распределения интенсивности при дифракции света на прямолинейном крае или на щели (дифракция Фраунгофера); состоит из двух симметричных ветвей, бесконечное число раз обвивающихся вокруг "фокусов" F и   и неограниченно приближающихся к ним.

Ур-ние К. с. в параметрич. форме имеет вид Френеля интегралов:

"фокусы"   и   - асимптотич. точки кривой; пределы интегрирования определяются размерами щелей и экранов, на к-рых происходит дифракция.

Относит. амплитуда волны при дифракции на крае экрана зависит от длины вектора, проведённого из точки F в разл. точки К. с. (напр., М₁ М₇). Скольжение вектора по правой (верх.) ветви спирали (FM_l, FH₂, FM₃)определяет плавно уменьшающуюся амплитуду волны в области геом. тени; амплитуда на границе тени соответствует вектору FO; скольжение вектора по левой (ниж.) части спирали (FM₄, FM₅, FM₆, FM₇,)даёт дифракц. полосы в освещённой области. Амплитуда волны в отсутствие экрана или вдали от границы геом. тени определяется вектором

11  Разрешающая способность дифракционной решетки Теперь мы способны понять еще ряд интересных явлений. Например, попробуем использовать решетку для определения длины волны света. На экране изображение щели развертывает­ся в целый спектр линий, поэтому с помощью дифракционной решетки можно разделить свет по составляющим его длинам волн. Возникает интересный вопрос: предположим, что имеются два источника с несколько разными частотами излучения или не­сколько разными длинами волн; насколько близкими должны быть эти частоты, чтобы по дифракционной картине нельзя было отделить одну частоту от другой? Красные и синие линии четко различаются. А вот если один луч красный, а другой чуть-чуть покраснее, самую малость. Насколько близки они должны быть? Ответ дается величиной, которая называется разрешающей спо­собностью решетки. Ниже мы используем один из способов ее определения. Предположим, что удалось найти дифракционный максимум для лучей определенного цвета, расположенный под некоторым углом. Если мы изменим длину волны, то и значение фазы (2pdsinq)/l будет иным и максимум, разумеется, возникнет при каком-то другом угле. Именно поэтому красные и синие полосы на экране разделяются. Насколько должны отличаться углы, что­бы мы смогли различить два разных максимума? Если верхушки максимумов совпадают, мы, конечно, не сможем различить их один от другого. Если же максимумы достаточно далеки друг от друга, то на картине распределения света возникают два горба.

Фиг. 30.6. Иллюстрация крите­рия Рэлея. Максимум одного распределения совпа­дает с минимумом другого. Чтобы заметить, когда начинает вырисовываться двойной горб, лучше всего воспользоваться простым правилом, называемым обычно правилом (иликритерием) Рэлея, (фиг. 30.6). По этому правилу первый минимум на дифракционной картине для одной длины волны должен совпадать с максимумом для другой длины волны. Теперь уже нетрудно вычислить разность длин волн, когда один минимум в точности «садится» на максимум другого пучка. Лучше всего для этого воспользоваться геометрическим способом.

Чтобы возник максимум при длине волны l', расстояние D (см. фиг. 30.3) должно быть равно nl', а чтобы возник мак­симум порядка m, расстояние D должно быть равно mnl'. Дру­гими словами, (2pd/l'), sinq=2pm и ndsinq, равное D, естьl', умноженная на тп, или соответственно mnl'. Если мы хотим, чтобы под тем же углом для другого луча с длиной волны l, появился минимум, расстояние D должно превышать тпl ровно на одну длину волны l, т. е. D=тпl+l =тпl'. Отсюда, полагая l'= l+dl,, получаем

Отношение l/dl, называется разрешающей способностью диф­ракционной решетки; она равна, как видно из формулы, пол­ному числу линий в решетке, умноженному на порядок макси­мума луча. Легко убедиться, что эта формула эквивалентна сле­дующему утверждению: разность частот должна быть равна обратной величине разности времен прохождения для самых крайних интерферирующих лучей sv=1/T Полезно запомнить именно эту общую формулу, потому что она применима не только для решеток, но и для любых устройств, тогда как вывод формулы (30.9) связан со свойствами дифрак­ционных решеток.

12 Френеля формулы определяют отношения амплитуды, фазы и состояния поляризации отражённой и преломленной световых волн, возникающих при прохождении света через неподвижную границу раздела двух прозрачных диэлектриков, к соответствующим характеристикам падающей волны. Установлены О. Ж. Френелем в 1823 на основе представлений об упругих поперечных колебаниях эфира. Однако те же самые соотношения — Френеля формулыследуют в результате строгого вывода из электромагнитной теории света при решении Максвелла уравнений и отождествлении световых колебаний с колебаниями вектора напряжённости электрического поля в световой волне, с которыми связано большинство эффектов волновой оптики.   Пусть плоская световая волна падает на границу раздела двух сред с преломления показателями n₁ и n₂. Углы j, j" и j" есть соответственно углы падения, отражения и преломления, причём всегда n₁sinj = n₂sinj"  (закон преломления) и ½j½ = ½j"½ (закон отражения). Электрический вектор падающей волны разложим на составляющую с амплитудой А_р , параллельную плоскости падения, и составляющую с амплитудой A_s , перпендикулярную плоскости падения. Аналогично разложим амплитуды отражённой волны на составляющие R_p и R_s , а преломленной волны — на D_p и D_s. Френеля формулы для этих амплитуд имеют вид:      (1)   Из (1) следует, что при любом значении углов j и j"  знаки A_p и D_p, а также знаки A_s и D_s совпадают. Это означает, что совпадают и фазы, т. е. во всех случаях преломленная волна сохраняет фазу падающей. Для компонент отражённой волны (R_p и R_s) фазовые соотношения зависят от j, n₁ и n₂. Так, если j = 0, то при n₂ > n₁ фаза отражённой волны сдвигается на p.   В экспериментах обычно измеряют не амплитуду световой волны, а её интенсивность, т. е. переносимый ею поток энергии, пропорциональный квадрату амплитуды (см. Пойнтинга вектор). Отношения средних за период потоков энергии в отражённой и преломленной волнах к среднему потоку энергии в падающей волне называется коэффициентом отражения r и коэффициентом прохождения d. Из (1) получим Френеля формулы, определяющие коэффициент отражения и прохождения для S- и р-составляющих падающей волны:      (2)   При отсутствии поглощения света r_s + d_s = 1 и r_p + d_p = 1, в соответствии с законом сохранения энергии. Если на границу раздела падает естественный свет (см. Поляризация света), т. е. все направления колебаний электрического вектора равновероятны, то половина энергии волны приходится на р-колебания, а вторая половина — на S-колебания; полный коэффициент отражения в этом случае: .   Если j" + j"  = 90° и tg (j" + j") ® ¥, r_p = 0, т. е. свет, поляризованный так, что его электрический вектор лежит в плоскости падения, в этих условиях совсем не отражается от поверхности раздела. Отражённый же свет (при падении естественного света под таким углом) будет полностью поляризован. Угол падения, при котором это происходит, называется углом полной поляризации или углом Брюстера (см. Брюстера закон). Для угла Брюстера справедливо соотношение tg j_Б = n₂/n₁.   При нормальном падении света на границу раздела двух сред (j = 0) Френеля формулы для амплитуд отражённой и преломленной волн могут быть приведены к виду      (3)   При этом исчезает различие между составляющими s и p, т.к. понятие плоскости падения теряет смысл. В этом случае, в частности, получаем ; .     (4)   Из (4) следует, что отражение света на границе раздела тем больше, чем больше абсолютная величина разности n₂ — n₁; коэффициенты r и d не зависят от того, с какой стороны границы раздела приходит падающая световая волна.   Условие применимости Френеля формулы — независимость показателя преломления среды от амплитуды вектора электрической напряжённости световой волны. Это условие, тривиальное в классической (линейной) оптике, не выполняется для световых потоков большой мощности, например излучаемых лазерами. В этих случаях Френеля формулы не дают удовлетворительного описания наблюдаемых явлений и необходимо использовать методы и понятиянелинейной оптики. См. также Отражение света. Оптика тонких слоев, Преломление света.   Лит.: Калитеевский Н. И., Волновая оптика, М., 1971; Борн М., Вольф Э., Основы оптики, пер. с англ., 2 изд., М., 1973; Ландсберг Г. С., Оптика, 5 изд., М., 1976 (Общий курс физики).   Л. Н. Капорский.     Расщепление падающего на границу двух диэлектрических сред луча света А на преломленный луч D и отраженный R. Для простоты показана ориентация только p-составляющих этих лучей, поляризованных параллельно плоскости падения.

13 Если естественный свет падает на границу раздела двух диэлектриков (например, воздуха и стекла), то часть его отражается, а часть преломляется и распространяется во второй среде. Устанавливая на пути отраженного и преломленного лучей анализатор (например, турмалин), убеждаемся в том, что отраженный и преломленный лучи частично поляризованы: при поворачивании анализатора вокруг лучей интенсивность света периодически усиливается и ослабевает (полного гашения не наблюдается!). Дальнейшие исследования показали, что в отраженном луче преобладают колебания, перпендикулярные плоскости падения (на рис. 275 они обозначены точками), в прелом ленном - колебания, параллельные плоскости падения (изображены с стрелками).

                       

                           

 Рис. 275

 

Степень поляризации (степень выделения световых волн с определенной ориентацией электрического (и магнитного) вектора) зависит от угла падения лучей и показателя преломления. Шотландский физик Д. Брюстер (1781-1868) установил закон, согласно которому при угле падения IB (угол Брюстера), определяемого соотношением

 

 (n₂₁ - показатель преломления второй среды относительно первой), отраженный луч является плоскополяризованным (содержит только колебания, перпендикулярные плоскости падения) (рис. 276). Преломленный же луч при угле падения i_B поляризуется максимально, но не полностью.

                                

 

                                                Рис. 276

 

Если свет падает на границу раздела под углом Брюстера, то отраженный и преломленный лучи взаимно перпендикулярны (tgi_B = sini_B/cosi_B, n₂₁ = sini_B / sini₂ (i₂ - угол преломления), откуда cosi_B = sini₂). Следовательно, i_B – i₂= p/2, но i¢_B = i_B (закон отражения), поэтому i'_B + i₂ = p/2. Степень поляризации отраженного и преломленного света при различных углах падения можно рассчитать из уравнений Максвелла, если учесть граничные условия для электромагнитного поля на границе раздела двух изотропных диэлектриков (так называемые формулы Френеля). Степень поляризации преломленного света может быть значительно повышена (многократным преломлением при условии падения света каждый раз на границу раздела под углом Брюстера). Если, например, для стекла (n = 1,53) степень поляризации преломленного луча составляет «15%, то после преломления на 8-10 наложенных друг на друга стеклянных пластинок вышедший из такой системы свет будет практически полностью поляризованным. Такая совокупность пластинок называется стопой. Стопа может служить для анализа поляризованного света как при его отражении, так и при его преломлении.

БРЮСТЕРА ЗАКОН - соотношение между показателем преломления n диэлектрика и таким углом падения   на него естественного (неполяризованного) света, при к-ром отражённый от поверхности диэлектрика свет полностью поляризован. При этом отражается только компонента   электрич. вектора световой волны, перпендикулярная плоскости падения, т. е. параллельная поверхности раздела; компонента  , лежащая в плоскости падения, не отражается, а преломляется (рис.). Это происходит при условии   . Угол  наз. углом Брюстера. Поскольку в силу закона преломления  , где   - угол преломления, то из Б. з. следует  , т. е. угол между отражённым и преломлённым лучами составляет 90°. Б. з. установлен Д. Брюстером (D. Brewster) в 1815.

Б. з. можно получить из Френеля формул для прохождения света через границу двух диэлектриков.