Графы. Основные понятия и определения.

Граф - первичное понятие. Граф задается двумя множествами: множеством вершин и множеством рёбер. Пример задания графа: G=G(X,A).

Если ребра графа ориентированы, то и сам граф ориентированный. Ребра-дуги. Если же ребра не ориентированы, то и сам граф является неориентированным.

В случае, когда мы имеем ориентированный граф, но пренебрегаем ориентацией его дуг, то мы называем его ориентированным дубликатом G=G(X,Ā)

Второй тип задания графа - задание множества вершин Х и отображение множества во множество Х. G=G(X, Г)

Пример:

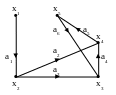
Рис.1

Если граф не ориентированный, и мы хотим представить его 2-м способом, то необходимо каждое ребро заменить 2 дугами, противоположно направленными (рис.2)

х₂

х₂

Рис.2

.

Две вершины x_i и x_j называются граничными дуги, если x_i – начало, а x_j – конец. Эти вершины называются смежными.

Две дуги а_i и а_j – смежные, если они различны, но имеют общую граничную точку.

Вершина изолирована, если она не соединена с другими вершинами графа.

Говорят, что дуга а_i исходит из вершины x_{i ,} если x_i начало, а не конец, и дуга заходит в вершину х_i , если х_i является концом дуги а_і, но не является началом (рис. 3)

a_i

a_i a_i x_i

x_i

x₁

Рис. 3

Общее число дуг, инцидентных вершине x_i, является степенью вершины и обозначается .

Вершины, степень которых больше 2, называются узлами.

Полустепень захода обозначает количество дуг, заходящих в вершину x_i, и обозначается .

Полустепень исхода обозначает количество дуг, исходящих из вершины x_i и обозначается .

Имеет смысл следующая формула: .

Вершина x_i называется входом, если , а .

x₁ a₁ x₂

a₂ a₄

a₃ x₃

x₅

a₅

x₄

не вход

вход

Рис. 4

Последовательность линий на графе.

Путем в графе называется такая последовательность дуг , в которой конец предыдущей дуги является началом последующей. Путь может быть конечным и бесконечным. Путь простой, если в нем ни одна дуга не встречается дважды. Путь составной, если в нем какая-либо из дуг встречается более одного раза.

Путь, проходящий через все вершины только 1 раз, называется Гамильтоновым.

Путь, содержащий все дуги графа по одному разу, называется Эйлеровым.

Длина пути – это число дуг последовательности

Ветвь – это путь, в котором начальная и конечная вершины являются узлами.

Дуга называется замыкающей, если ее удаление из графа не приведет к аннулированию пути

x₁ x₃ x₅

x₂ x₄

-замыкающая ветвь

Рис. 5

Контур- это конечный путь, начинающийся и заканчивающийся одной и той же вершиной.

Контур единичной длины называется петлей.

x₁

Рис.6

На контур распространяются все определения, введенные для пути.

Все раннее приведенные понятия, рассмотрены на примере ориентированных графов.

В случае неориентированных графов, существуют аналогичные понятие, которые имеют другие названия.

Ориентированный граф	Неориентированный граф
Дуга	Ребро
Путь	Цепь
Контур	Цикл

Виды графов

G=G(X, A) - нуль-граф, если он состоит только из изолированных вершин. Справедливо соотношение

Если степень всех вершин графа одинакова, то этот граф однородный.

x₂

x₁ x₃

x₄

однородный граф

Рис.6

Граф G(X,A), в котором любые две смежные вершины соединены двумя противоположно ориентированными дугами, называется симметрическим (рис.7).

x₂

x₁ x₃

Рис.7

x₂

x₁ x₃

x₄

Граф G(X, A) без петель, в котором каждая пара вершин соединена одинаковым количеством дуг, называется полным. Так как каждая вершина полного графа соединена дугой с остальными вершинами, то степени всех вершин полного графа получаются одинаковыми. Обратное этому утверждение не верно.

||- Гамильтонов путь

Рис.8

В полном графе всегда имеется Гамильтонов путь.

Если хотя бы 2 вершины соединены более чем 1 дугой (ребром), то это мультиграф. Наибольшее количество дуг (ребер), соединяющих смежные вершины в мультиграфе, называется его кратностью.

М

x₃ x₄ x₆

x₁ x₂ x₃

ультиграф Р-граф, Р-кратность. Например:

Рис.9

Изоморфизм

Два графа G₁ и G₂ – изоморфные, если существует взаимнооднозначное соответствие между множествами их вершин, обладающее тем свойством, что число ребер, соединяющих любые 2 вершины в графе G₁ , равно числу ребер соединяющих соответствующие вершины в графе G₂ (рис.10)

х₁ х₂ х₃ х₁ х₄

х₆ х₂

х₄ х₅ х₆ х₃ х₅

Рис.10

Для ориентированных графов еще необходимо выполнение условия .

Г

x₂ x₅ x₃ x₅

x₆

x₃ x₂ x₆

x₁

x₄ x₁ x₄

раф, который можно изобразить на плоскости так, чтобы 2 ребра не пересекались в точках, отличных от вершин, называется плоским графом.

Изоморфный граф

Рис.11

Грань плоского графа - область плоскости, ограниченная ребрами и не содержащая в себе ни вершин, ни ребер. Число граней находится по формуле , где m-число ребер, а n-число вершин графа.

Неограниченная область плоскости, лежащая за пределами графа, называется бесконечной гранью. Все остальные грани - конечные.

Две грани смежные, если их края имеют хотя бы одно общее ребро. Грани, которые соприкасаются в отдельных вершинах - не смежные.

Для плоского графа можно построить двойственный ему граф G^*, используя 3 правила:

1. Определить число граней исходного графа с учетом внешней грани.

2. В каждой грани графа G ставится вершина графа G^*. Петля исходного графа рассматривается как грань.

3. Вершина графа G^* соединяется ребрами в том случае, если они лежат на гранях, имеющих общее ребро, причем ребро, соединяющее эти 2 вершины двойственного графа, должно обязательно проходить через общее ребро исходного графа. Если у 2 граней, на которых лежат вершины графа G^* , имеется несколько общих ребер, то эти вершины соединяются столькими ребрами, сколько общих ребер имеет грань. Это справедливо как для внешних, так и для внутренних граней. Висячему ребру исходного графа соответствует петля в графе G^*, которая проведена из вершины внешней грани двойственного графа таким образом, чтобы висячая вершина оказалась внутри этой петли (рис.12)

– висячее ребро

исходный граф G

двойственный граф G^*

Рис.12

Подмножество графов

Подграфом графа G(X,Г) называется граф G(B, Г_В), определяемый следующим образом:

1. Множество вершин В подграфа являются некоторым подмножеством вершин графа G(X, Г), .

2. Отображением каждой вершины подграфа является пересечение отображения той же вершины графа G(X,Г) со всем подмножеством вершин В, .

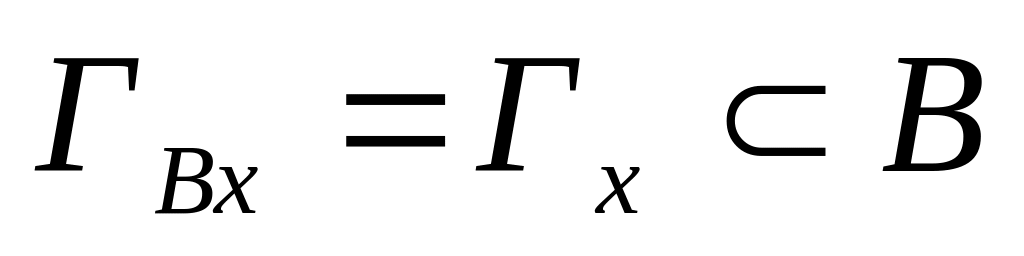В этом примере мы изобразим схему построения подграфа G(B,Г_В) для заданного графа G(X,Г) (рис. 13)

Задание: «Построить подграф ». Иллюстрация этой задачи приведена выше.

Частичным графом для графа G(X, Г) называется граф G(X, F), в котором содержатся все вершины исходного графа и некоторое подмножество дуг исходного графа . То есть, от исходного графа сохраняются вершины и некоторые дуги.

Частичным подграфом графа G(X, Г) называется граф G(B, Г), в котором вершины В являются подмножеством вершин Х, а отображение F меньше пересечения отображений исходного графа со всеми вершинами частичного подграфа G(B, F), то есть:

2. 

Фактором графа G(X,Г) называется частичный граф, в котором каждая вершина обладает полустепенями захода и исхода равными 1.

Базисным графом называется ориентированный частичный граф, образованный из исходного удалением петель и замыкающих дуг (рис.14)

x₁ x₂ x₁ x₂

x₃ x₃

x₆ x₄ x₆ x₄

x₇ x₅ x₇ x₅

Рис.14