6. Формулы Крамера для решения системы линейных уравнений.
Метод Крамера состоит в том, что мы последовательно находим главный определитель системы (5.3), т.е. определитель матрицы А
D = det (ai j)
и n
вспомогательных определителей D i (i=
),
которые получаются из определителя D заменой
i-го столбца столбцом свободных членов.
Формулы Крамера имеют вид:
D × x i = D i ( i = ). (5.4)
Из (5.4) следует правило Крамера, которое дает исчерпывающий ответ на вопрос о совместности системы (5.3): если главный определитель системы отличен от нуля, то система имеет единственное решение, определяемое по формулам:
x i = D i / D.
Если главный определитель системы D и все вспомогательные определители D i = 0 (i= ), то система имеет бесчисленное множество решений. Если главный определитель системы D = 0, а хотя бы один вспомогательный определитель отличен от нуля, то система несовместна.
Пример 2.14. Решить методом Крамера систему уравнений:
x1 + x2 + x3 + x4 = 5,
x1 + 2x2 - x3 + 4x4 = -2,
2x1 - 3x2 - x3 - 5x4 = -2,
3x1 + x2 +2x3 + 11 x4 = 0.
Решение. Главный определитель этой системы
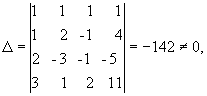
значит,
система имеет единственное решение.
Вычислим вспомогательные определители D i (
i = 
),
получающиеся из определителя D путем
замены в нем столбца, состоящего из
коэффициентов при xi, столбцом
из свободных членов:
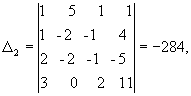
Отсюда x1 = D 1/D = 1, x2 = D 2/D = 2, x3 = D 3/D = 3, x4 = D 4/D = -1, решение системы - вектор С=(1, 2, 3, -1)T.
7. Обратная матрица и ее вычисление.
Обра́тная ма́трица — такая матрица A−1, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:
Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матрицобратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.
Свойства обратной матрицы
,
где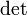 
обозначает определитель.
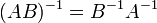для
любых двух обратимых матриц A и B.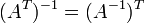
где * T обозначает
транспонированную матрицу.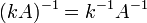
для
любого коэффициента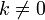 
.Если необходимо решить систему линейных уравнений Ax = b, (b — ненулевой вектор) где x — искомый вектор, и если A − 1 существует, то x = A − 1b. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.
8. Свойства обратной матрицы и новый вывод формул Крамера.
9. Определение n-мерных арифметических векторов и действий над ними.
Вектор.
Определение. Упорядоченную
совокупность ( x 1,
x 2,
... , x n )
n вещественных чисел называют n-мерным
вектором,
а числа x i (
i = 
)
- компонентами, или координатами, вектора.
Пусть
даны векторы 
и 
.
Определение. Суммой
векторов 
и 
называется
вектор 
,
т.е. при сложении векторов их соответствующие
координаты складываются: (2, –4) + (–2, 4)
= (0, 0); (3,0,1) + (0,1,4)+(–1, –7,0) = (2,
–6,5).
Определение. Произведением
вектора 
на
число 
называется
вектор 
т.е.
при умножении вектора на число каждая
его координата умножается на это
число.
Можно проверить,
что введенные таким образом операции
над векторами удовлетворяют всем
свойствам операций в линейном пространстве.
Следовательно, арифметическое n-мерное
пространство Rn является
частным случаем введенного ранее
линейного пространства.
Определение. Скалярным
произведением двух векторов 
и 
называется
число, равное сумме произведений
соответствующих координат
векторов: 
Пример: Пусть 
и 
.
Тогда 
.
Скалярное произведение обладает
следующими свойствами:
1.
,
причем 
,
только
при 
2.
,
3.
,
4.
.
Определение. Два
вектора называются ортогональными,
если их скалярное произведение равно
0,
т.е. 
.
Пример. Пусть 
Тогда 
ортогональны.
Определение. Линейное
пространство с введенным скалярным
произведением называется евклидовым n-мерным
пространством.
Примеры:
1. Множество трехмерных векторов
R3.
2.
Множество двумерных векторов
R2.
3.
Множество R1 =
R – множество действительных чисел.