Четыре теоремы о дифференцируемых функциях

В этом разделе мы рассмотрим некоторые утверждения, касающиеся функций, которые во всех точках данного множества имеют производную. Такие функции называютсядифференцируемыми на данном множестве.

Первая теорема имеет вспомогательный характер для дальнейшего, хотя важна и сама по себе.

Пусть функция   определена на некотором множестве  , и  . Назовём точку   точкой максимума функции   на множестве  , если при всех   выполняется неравенство  , и точкой минимума, если при всех   выполняется неравенство  .

Точка  , являющаяся либо точкой максимума, либо точкой минимума, называется точкой экстремума.

        Теорема 5.1 (Ферма)   Пусть функция   имеет на множестве   точку экстремума  , причём множество   содержит некоторую  -окрестность  точки  . Тогда либо   имеет в точке   производную, равную 0, то есть  , либо производная в точке   не существует.

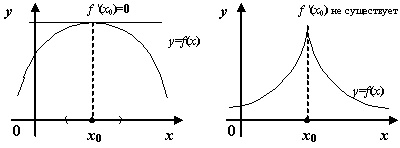
Рис.5.1.Поведение функции в окрестности точки экстремума

        Замечание 5.1   Заметим, что условие   означает, что тангенс угла   наклона касательной к графику  , проведённой при  , равен 0. Отсюда  , то есть теорема Ферма утверждает, что касательная, проведённая в точке экстремума, горизонтальна (если эта касательная существует).     

        Доказательство теоремы Ферма.     Если производная в точке экстремума не существует, то утверждение теоремы верно. Предположим, что производная   существует. Рассмотрим два случая.

Пусть функция имеет в точке   максимум. Тогда   при всех  , поскольку  . Если взять  , то  , и поэтому 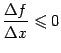 . При вычислении производной мы переходим к пределу при   в этом разностном отношении. При этом знак нестрогого неравенства сохраняется, когда мы берём предел справа:

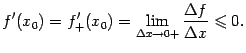
Аналогично, при  ,  , и поэтому 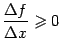 . Отсюда, вычисляя предел слева, получаем:

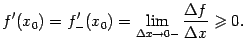
Итак, выполняются два неравенства:   и  , что возможно лишь при  .

Пусть теперь функция   имеет в точке   минимум. Тогда   при всех  , поскольку  . Если взять  , то  , и поэтому . Переходя к пределу при   в разностном отношении, получаем:

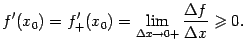
Аналогично, при  ,  , и поэтому  . Вычисляя предел слева, получаем:

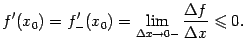
Из неравенств   и   получаем, что  .      

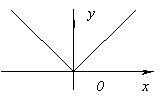
        Пример 5.1   Функция   имеет на отрезке   точку минимума  . Производная функции существует при всех  :  . В точке минимума производная, действительно, оказывается равной 0:  , так что утверждение теоремы Ферма выполнено.     

Рис.5.2.График 

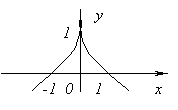
        Пример 5.2   Функция   имеет на отрезке   точку минимума  . Производная функции при   не существует. (Производная существует при всех  , она равна 1 при   и   при  .) Итак, в точке минимума этой функции производная не существует, и утверждение теоремы Ферма снова выполнено.     

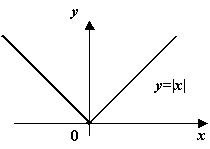
Рис.5.3.График 

Далее мы будем предполагать, что функция  , заданная на отрезке  , удовлетворяет следующим условиям: она непрерывна на отрезке   и дифференцируема на интервале  ; существование односторонних производных в точках   и  , вообще говоря, не предполагается. Непрерывность во всех внутренних точках отрезка, конечно, следует из предположенной дифференцируемости, а вот непрерывность в точках   (непрерывность справа) и   (непрерывность слева) из дифференцируемости в точках интервала не следует.

        Теорема 5.2 (Ролля)   Пусть функция   дифференцируема на интервале  , непрерывна в точках   и   и принимает в этих точках значение 0:  . Тогда найдётся хотя бы одна точка  , в которой  .

        Замечание 5.2   Это утверждение можно переформулировать так: между двумя корнями   и   дифференцируемой функции   обязательно найдётся корень её производной   (то есть точка  , такая что  ). Условие   означает, что касательная, проведённая к графику   при  , расположена горизонтально.

Заметим также, что теорема Ролля не утверждает, что корень   -- единственный корень производной на интервале  ; на этом интервале может находиться несколько корней производной.     

Рис.5.4.Между двумя корнями дифференцируемой функции лежит хотя бы один корень её производной

        Доказательство теоремы Ролля.     Так как при наших предположениях функция   непрерывна на отрезке  , то она принимает своё максимальное значение   и минимальное значение   в некоторых точках   и   этого отрезка.

Рассмотрим два случая. Если  , то наибольшее и наименьшее значения функции совпадают, и, следовательно, функция постоянна на отрезке  :  . Значит,   при всех  , и в качестве   в этом случае можно взять любую точку   интервала  .

Если же  , то либо  , либо   отлично от 0 и, следовательно, либо точка  , либо точка   не совпадает с концами отрезка   и  , то есть лежит внутри интервала  . Пусть, для определённости,   -- внутренняя точка интервала. Тогда, по теореме Ферма,  , поскольку по предположению доказываемой теоремы,   имеет производную во всех точках интервала   и, следовательно, в точке  . Итак, в этом случае точку   можно взять в качестве искомой точки  : тогда  .      

        Теорема 5.3 (Лагранжа)   Пусть функция   дифференцируема на интервале   и непрерывна в точках   и  . Тогда найдётся такая точка  , что

(5.1)

        Замечание 5.3   Формулу (5.1) можно записать в виде

(5.2)

Если считать, что аргументу   придано приращение  , то функция получает приращение  . (При этом мы не считаем, что   и   стремятся к 0, то есть это конечные, а не бесконечно малые, приращения.) При этих обозначениях формулу (5.2) мы можем записать в виде

в котором участвуют конечные приращения аргумента и функции. Поэтому формулу (5.2) называют формулой конечных приращений.     

        Доказательство теоремы Лагранжа.     Дадим сначала геометрическую иллюстрацию теоремы. Соединим конечные точки графика   на отрезке   хордой. Конечные приращения   и   -- это величины катетов треугольника, гипотенузой которого служит проведённая хорда. 

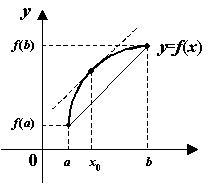
Рис.5.5.Касательная в некоторой точке параллельна хорде

Отношение конечных приращений   и   -- это тангенс угла наклона хорды. Теорема утверждает, что к графику дифференцируемой функции можно провести в некоторой точке  касательную, которая будет параллельна хорде, то есть угол наклона касательной   (  ) будет равен углу наклона хорды   ( 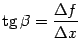 ). Но наличие такой касательной геометрически очевидно.

Заметим, что проведённая хорда, соединяющая точки   и   -- это график линейной функции  . Поскольку угловой коэффициент этой линейной функции равен, очевидно,  , то

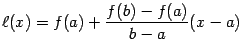
(мы учли то, что график линейной функции проходит через точку  ).

Сведём доказательство к применению теоремы Ролля. Для этого введём вспомогательную функцию  , то есть

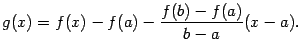
Заметим, что   и   (по построению функции  ). Так как линейная функция   дифференцируема при всех  , то функция   удовлетворяет, тем самым, всем свойствам, перечисленным в условии теоремы Ролля. Поэтому найдётся такая точка  , что  .

Заметим теперь, что

Значит, равенство   можно переписать в виде

Таким образом, мы доказали формулу (5.1).      

Из теоремы Лагранжа вытекает утверждение, обратное к тому, что производная постоянной есть 0, а именно:

        Следствие 5.1   Пусть на интервале   функция   имеет производную  , тождественно равную 0:  . Тогда   на интервале  .

        Доказательство.     Заметим для начала, что непрерывность функции   в любой точке интервала   следует из дифференцируемости в этой точке. Значит, теорему Лагранжа можно применить к функции   на любом отрезке  .

Возьмём любые две точки  , такие что  , и выпишем для функции   на отрезке   формулу конечных приращений:  , при некотором  . Но в любой точке производная по предположению равна 0, в том числе  . Отсюда  , или  . Обозначим это общее значение через  . Выбирая произвольно точку  , получим, что   при всех  ; выбирая произвольно точку  , -- что   при всех  . Но это означает, что  при всех  .      

        Теорема 5.4 (Коши)   Пусть функции   и   дифференцируемы на интервале   и непрерывны при   и  , причём   при всех  . Тогда в интервале   найдётся такая точка  , что

        Доказательство.     Докажем сначала, что  , то есть что дробь в левой части формулы имеет смысл. Действительно, для этой разности можно записать формулу конечных приращений:

при некотором  . Но в правой части этой формулы оба множителя отличны от нуля.

Для доказательства теоремы применим тот же приём, что при доказательстве теоремы Лагранжа: введём вспомогательную функцию

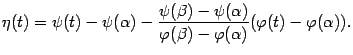
Функция  , очевидно, является дифференцируемой при всех   и непрерывной в точках   и  , поскольку этими свойствами обладают функции   и  . Кроме того, очевидно, что при   получается  . Покажем, что и  :

Значит, функция   удовлетворяет на отрезке   условиям теоремы Ролля. Поэтому существует такая точка  , что  .

Вычислим теперь производную функции  :

Получаем, что

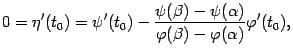
откуда получаем утверждение теоремы:

     

        Замечание 5.4   Можно считать функции   и   координатами движущейся на плоскости   точки, которая описывает линию  , соединяющую начальную точку   с конечной точкой  . (Тогда уравнения   и   параметрически задают некоторую зависимость  , графиком которой служит линия  .) 

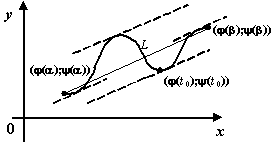
Рис.5.6.Хорда параллельна некоторой касательной к кривой

Отношение 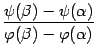 , как нетрудно видеть из чертежа, задаёт тогда угловой коэффициент хорды, соединяющей точки   и  . В то же время, по формуле производной функции, заданной параметрически, имеем:  . Значит, дробь   -- это угловой коэффициент касательной к линии   в некоторой точке  . Тем самым утверждение теоремы означает, с геометрической точки зрения, что на линии   найдётся точка, такая что проведённая в этой точке касательная параллельна хорде, соединяющей крайние точки линии. Но это -- то же самое утверждение, которое составляло геометрический смысл теоремы Лагранжа. Только в теореме Лагранжа линия   была задана явной зависимостью  , а в теореме Коши -- зависимостью, заданной в параметрической форме.     

14

еорема (правило Лопиталя). Пусть функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a, и пусть   или  . Тогда, если существует предел отношения производных этих функций  , то существует и предел отношения самих функций f(x)/g(x) при x→а, причем

(1)

Таким образом, коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.

Замечание. Отметим, что формула (1) справедлива только в том случае, если предел, стоящий справа, существует. Может случиться, что предел, стоящий слева существует, в то время как предел, стоящий в правой части равенства, не существует.

Например, найти  . Этот предел существует  . Но отношение производных(1+cosx)/1=1+cos x при x→∞ не стремится ни к какому пределу.

Заметим, что если отношение производных опять представляет собой неопределенность вида 0/0 или ∞/∞, то можно снова применить сформулированную теорему, то есть перейти к отношению вторых производных и так далее.

Вспомним, что к этим двум случаям сводятся случаи других неопределенностей: ∞·∞; 0·∞.

Для раскрытия неопределенностей 1^∞, 1⁰, ∞⁰ нужно прологарифмировать данную функцию и найти предел ее логарифма.

Примеры.

1. .

2. .

3. .

4. 

5. 

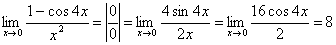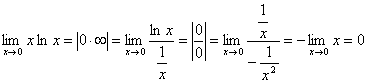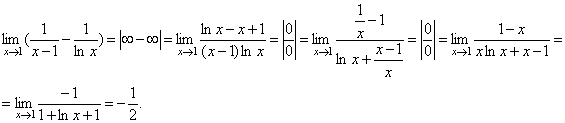
Обозначим  .

Прологарифмируем это равенство  . Найдем  .

Так как lny функция непрерывная, то  . Следовательно,   или  .

15

Р ассмотрим график непрерывной функции y=f(x), изображенной на рисунке. Значение функции в точке x₁ будет больше значений функции во всех соседних точках как слева, так и справа от x₁. В этом случае говорят, что функция имеет в точке x₁ максимум. В точке x₃ функция, очевидно, также имеет максимум. Если рассмотреть точку x₂, то в ней значение функции меньше всех соседних значений. В этом случае говорят, что функция имеет в точке x₂ минимум. Аналогично для точки x₄.

Функция y=f(x) в точке x₀ имеет максимум, если значение функции в этой точке больше, чем ее значения во всех точках некоторого интервала, содержащего точку x₀, т.е. если существует такая окрестность точки x₀, что для всех x≠x₀, принадлежащих этой окрестности, имеет место неравенство f(x)<f(x₀).

Функция y=f(x) имеет минимум в точке x₀, если существует такая окрестность точки x₀, что для всех x≠x₀, принадлежащих этой окрестности, имеет место неравенство f(x)>f(x₀.

Точки, в которых функция достигает максимума и минимума, называются точками экстремума, а значения функции в этих точках экстремумами функции.

Обратим внимание на то, что функция, определенная на отрезке, может достигать максимума и минимума только в точках, заключенных внутри рассматриваемого отрезка.

Отмети, что если функция имеет в точке максимум, то это не означает, что в этой точке функция имеет наибольшее значение во всей области определения. На рисунке, рассмотренном выше, функция в точке x₁ имеет максимум, хотя есть точки, в которых значения функции больше, чем в точке x₁. В частности, f(x₁) < f(x₄) т.е. минимум функции больше максимума. Из определения максимума следует только, что это самое большое значение функции в точках, достаточно близкихк точке максимума.

Теорема 1. (Необходимое условие существования экстремума.) Если дифференцируемая функция y=f(x) имеет в точке x= x₀ экстремум, то ее производная в этой точке обращается в нуль.

Доказательство. Пусть для определенности в точке x₀ функция имеет максимум. Тогда при достаточно малых приращениях Δxимеем f(x₀+ Δx)<f(x₀), т.е.   Но тогда

Переходя в этих неравенствах к пределу при Δx→ 0 и учитывая, что производная f '(x₀) существует, а следовательно предел, стоящий слева, не зависит от того как Δx → 0, получаем: при Δx → 0 – 0 f'(x₀) ≥ 0 а при Δx → 0 + 0 f'(x₀) ≤ 0. Так как f '(x₀) определяет число, то эти два неравенства совместны только в том случае, когда f '(x₀) = 0.

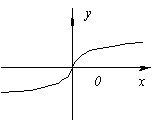
Доказанная теорема утверждает, что точки максимума и минимума могут находиться только среди тех значений аргумента, при которых производная обращается в нуль. Мы рассмотрели случай, когда функция во всех точках некоторого отрезка имеет производную. Как же обстоит дело в тех случаях, когда производная не существует? Рассмотрим примеры. Примеры. y=|x|. Функция не имеет производной в точке x=0 (в этой точке график функции не имеет определенной касательной), но в этой точке функция имеет минимум, так как y(0)=0, а при всехx≠ 0y > 0.   Функция   не имеет производной при x=0, так как   обращается в бесконечность приx=0. Но в этой точке функция имеет максимум.   Функция   не имеет производной при x=0, так как   при x→0. В этой точке функция не имеет ни максимума, ни минимума. Действительно, f(x)=0 и при x<0f(x)<0, а приx>0f(x)>0. Таким образом, из приведенных примеров и сформулированной теоремы видно, что функция может иметь экстремум лишь в двух случаях: 1) в точках, где производная существует и равна нулю; 2) в точке, где производная не существует. Однако, если в некоторой точке x0 мы знаем, что f '(x0)=0, то отсюда нельзя делать вывод, что в точке x0 функция имеет экстремум. 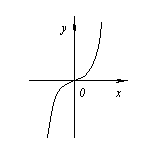Например.  . Но точка x=0 не является точкой экстремума, поскольку слева от этой точки значения функции расположены ниже оси Ox, а справа выше. Значения аргумента из области определения функции, при которых производная функции обращается в нуль или не существует, называются критическими точками.

Из всего вышесказанного следует, что точки экстремума функции находятся среди критических точек, и, однако, не всякая критическая точка является точкой экстремума. Поэтому, чтобы найти экстремум функции, нужно найти все критические точки функции, а затем каждую из этих точек исследовать отдельно на максимум и минимум. Для этого служит следующая теорема.

Теорема 2. (Достаточное условие существования экстремума.) Пусть функция непрерывна на некотором интервале, содержащем критическую точку x₀, и дифференцируема во всех точках этого интервала (кроме, быть может, самой точки x₀). Если при переходе слева направо через эту точку производная меняет знак с плюса на минус, то в точке x = x₀ функция имеет максимум. Если же при переходе через x₀ слева направо производная меняет знак с минуса на плюс, то функция имеет в этой точке минимум.

Таким образом, если

1. f '(x)>0 при x<x₀ и f '(x)<0 при x> x₀, то x₀ – точка максимума;

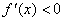2.  при x<x₀ и f '(x)>0 при x> x₀, то x₀ – точка минимума.

Доказательство. Предположим сначала, что при переходе через x₀ производная меняет знак с плюса на минус, т.е. при всех x, близких к точке x₀ f '(x)>0 для x< x₀, f '(x)<0 для x> x₀. Применим теорему Лагранжа к разности f(x) - f(x₀) = f '(c)(x- x₀), где cлежит между x и x₀.

1. Пусть x < x₀. Тогда c< x₀ и f '(c)>0. Поэтомуf '(c)(x- x₀)<0и, следовательно,

f(x) - f(x₀)<0,т.е. f(x)< f(x₀).

2. Пусть x > x₀. Тогда c> x₀ и f '(c)<0. Значитf '(c)(x- x₀)<0. Поэтому f(x) - f(x₀)<0,т.е.f(x) < f(x₀).

Таким образом, для всех значений x достаточно близких к x₀ f(x) < f(x₀). А это значит, что в точке x₀ функция имеет максимум.

Аналогично доказывается вторая часть теоремы о минимуме.

П роиллюстрируем смысл этой теоремы на рисунке. Пусть f '(x₁)=0 и для любых x,достаточно близких к x₁, выполняются неравенства

f '(x)<0 при x< x₁, f '(x)>0 при x> x₁.

Тогда слева от точки x₁ функция возрастает, а справа убывает, следовательно, при x = x₁функция переходит от возрастания к убыванию, то есть имеет максимум.

Аналогично можно рассматривать точки x₂ и x₃.

Схематически все вышесказанное можно изобразить на картинке:

Правило исследования функции y=f(x) на экстремум

1. Найти область определения функции f(x).

2. Найти первую производную функции f '(x).

3. Определить критические точки, для этого:

   1. найти действительные корни уравнения f '(x)=0;

   2. найти все значения x при которых производная f '(x) не существует.

4. Определить знак производной слева и справа от критической точки. Так как знак производной остается постоянным между двумя критическими точками, то достаточно определить знак производной в какой-либо одной точке слева и в одной точке справа от критической точки.

5. Вычислить значение функции в точках экстремума.

16