Глава 3 Прямая в пространстве

§1 Различные виды уравнения прямой в пространстве

1 Каноническое уравнение прямой , проходящей через данную точку параллельно вектору

(27)

Рисунок 45

Вектор называют направляющим вектором для прямой . Обращение в нуль одного из знаменателей уравнения (27) означает обращение в нуль соответствующего числителя.

2 Параметрическое уравнение прямой : , (28)

где - переменный параметр, .

В векторной форме уравнение (28) имеет вид , где , .

3 Уравнение прямой, проходящей через две точки и , где ( , , одновременно), имеет вид

(29)

Рисунок 46

4 Общее уравнение прямой, которое задается пересечением двух плоскостей:

(коэффициенты при переменных не пропорциональны). Направляющий вектор прямой (27) находится по формуле

или , т.е. (30)

Рисунок 47

§2 Угол между двумя прямыми в пространстве. Условия параллельности и перпендикулярности прямых в пространстве. Условие компланарности двух прямых в пространстве

Пусть прямые и заданы уравнениями:

и .

Под углом между прямыми понимают угол между их направляющими векторами и .

Рисунок 48

Для нахождения острого угла между прямыми и используют формулу вида:

(31)

Условие перпендикулярности двух прямых в пространстве:

Д ве прямые в пространстве перпендикулярны тогда и только тогда, когда их направляющие вектора перпендикулярны, т.е.

(32)

Рисунок 49

Условие параллельности двух прямых в пространстве:

Две прямые в пространстве параллельны тогда и только тогда, когда их направляющие векторы коллинеарны, т.е.

(33)

Рисунок 50

Условием, при котором две прямые и лежат в одной плоскости, является равенство

, (34)

п ри этом, если || , то прямые и пересекаются.

Практическое занятие № 3

Уравнения прямой в пространстве. Способы задания прямой в пространстве. Взаимное расположение прямых в пространстве.

Задача 1 Составить каноническое уравнение прямой, проходящей через

а) точку , параллельной вектору ;

б) точку , параллельной прямой ;

в) точку , параллельной оси ;

г) точки и ;

д) точку , параллельной прямой являющейся пересечением двух плоскостей

Решение.

а ) Канонические уравнения прямой , проходящей через данную точку параллельно вектору , имеют вид . По условию задачи точка лежащая на прямой задана координатами и направляющий вектор имеет координаты , тогда составим уравнения прямой

Рисунок 51

б ) уравнение прямой, проходящей через точку , параллельной прямой . Так как прямые, по условию задачи, и параллельны, то направляющие вектора их коллинеарны. Тогда направляющим вектором для прямой может быть вектор . Используя предыдущую формулу , составим уравнение прямой.

Уравнение прямой, проходящей через точку с направляющим вектором будет иметь вид Рисунок 52 .

в) уравнение прямой, проходящей через точку , параллельной оси . Для каждого случая составим канонические уравнения проходящие через точку с направляющими векторами , , . . Перейдем от канонического уравнения к параметрическому уравнению.

г) уравнение прямой, проходящей через две различные точки и задано формулой: . Точки лежащие на прямой имеют координаты и , подставляя в формулу получим уравнения : , .

д) уравнение прямой, проходящей через точку , параллельной прямой являющейся пересечением двух плоскостей

С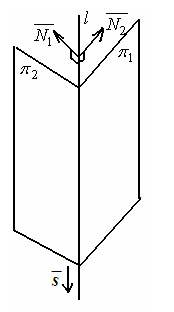 оставим каноническое уравнения прямой по формуле и проходящей через точку с координатами . По условию задачи прямая задается пересечением двух плоскостей:

Н ормальные вектора двух плоскостей будут перпендикулярны этой прямой , следовательно, перпендикулярны и направляющему

вектору этой прямой . Тогда уравнение прямой,

Рисунок 53 проходящей через точку с направляющим вектором :

.

Задача 2 Найти угол между двумя прямыми и :

а) , ;

б) , , , , , ;

в)

Решение.

В пространстве угол между двумя прямыми равен углу между их направляющими векторами.

а) , .

Выпишем направляющие вектора двух прямых и : , . Используя данную формулу найдем угол между двумя прямыми и :

.

б) прямыми и заданы в параметрическом виде, выпишем направляющие вектора двух прямых и :

; .

По предыдущей формуле найдем угол: .

в)

Для данных прямых, которые заданы пересечением двух плоскостей найдем направляющие вектора:

: .

: , .

.

Задача 3 Установить взаимное расположение прямых и :

а) и

б) и .

Решение.

а) Выпишем направляющие векторы первой и второй прямых: , . Как видно, координаты этих векторов пропорциональны:

.

Следовательно, данные прямые параллельные или совпадают. Возьмем на первой прямой какую-нибудь точку, например точку . Подставим ее координаты в уравнение второй прямой:

Получаем - из первого уравнения, - из второго, - из третьего. Это означает, что точка не принадлежит второй прямой; прямые не совпадают, значит они параллельны.

б) и . Координаты направляющих векторов и данных прямых не пропорциональны. Следовательно, прямые либо пересекающиеся, либо скрещивающиеся. Проверим выполнение условия (34) принадлежности двух прямых одной плоскости, предварительно выписав координаты точек и , через которые проходят данные прямые: , . Имеем

.

Следовательно, данные прямые – скрещивающиеся.

Задача 4 Уравнение прямой

преобразовать к каноническому виду.

Решение.

Для решения этой задачи надо знать какую-либо точку прямой и ее направляющий вектор . Выберем точку на прямой следующим образом: положим, например, ; тогда для определения абсциссы и ординаты у этой точки решим следующую систему уравнений

из которой находим , . Итак, на прямой известна точка . Направляющий вектор прямой находим по формуле:

, т.е. .

Тогда, согласно формуле ,

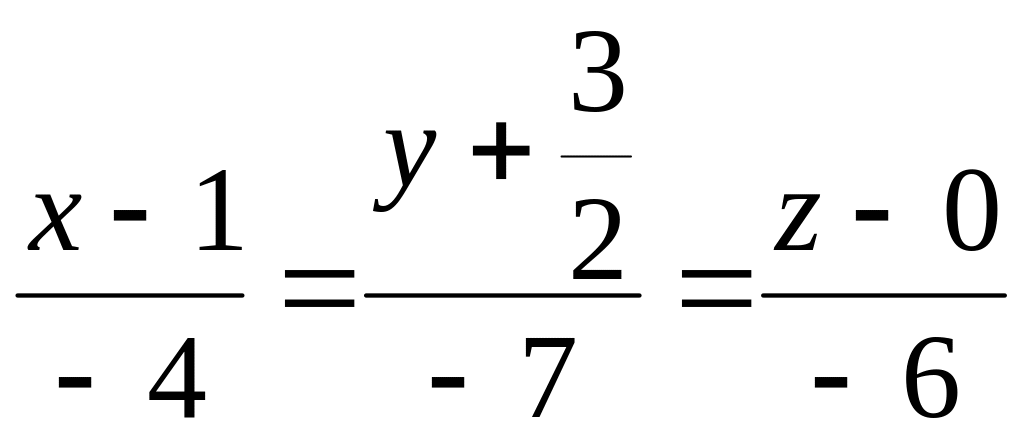или – искомое уравнение прямой .

Задача 5 Составить параметрические уравнения прямой перпендикулярной плоскости и проходящей через точку .

Решение.

Вектор перпендикулярен плоскости . Следовательно, в качестве вектора можно взять вектор , т.е. . Тогда параметрическое уравнения прямой, перпендикулярной плоскости , примет вид

Ответ.