
- •Билет №1. Доказать теорему Ролля.
- •Определена и непрерывна на отрезке .
- •1) Пеано
- •1) Пеано
- •Доказать теорему о связи функции, её предела и бесконечно малой.
- •Билет №5. Доказать второе достаточное условие экстремума.
- •Вывести уравнение наклонной асимптоты.
- •Билет №6. Доказать необходимое условие возрастания дифференцируемой функции.
- •Предел числовой последовательности. Сформулировать признак сходимости монотонной последовательности. Доказать теорему о единственности предела.
- •Билет №7. Доказать необходимое условие экстремума дифференцируемой функции.
- •Вывести 1 замечательный предел:
- •Билет №8-1. Доказать теорему Бернулли-Лопиталя для предела отношения двух бесконечно малых функций.
- •Билет №8-2. Векторная функция скалярного аргумента: и её производная. Касательная к пространственной кривой. Теорема о производной вектор-функции постоянной длины.
- •Билет №9-1. Формула Тейлора с остаточным членом в форме Пеано, Лагранджа.
- •Дифференциал функции – определение, геометрический смысл. Доказать инвариантность формы дифференциала первого порядка.
- •Билет №11. Доказать второе достаточное условие экстремума.
- •Доказать теорему о пределе произведения функций.
- •Билет №12. Доказать достаточное условие выпуклости графика функции.
- •Доказать теорему о знакопостоянстве функции, имеющей отличный от нуля предел.
- •Билет №13. Необходимое и достаточное условие существования точки перегиба графика функции. Доказать необходимое условие.
- •Определена и непрерывна на отрезке .
- •Дифференцируема на интервале .
- •И на концах отрезка принимает одинаковые значения.
- •Доказать теорему о связи функции, её предела и бесконечно малой.
- •Билет №21. Формула Маклорена для с остаточным членом в форме Пеано.
- •1) Пеано
- •Сформулировать определение функции, непрерывной на отрезке. Основные теоремы о функциях, непрерывных на отрезке.
- •Билет №22. Доказать первое достаточное условие экстремума функции.
- •Вывести 1 замечательный предел:
- •Билет №23. Доказать второе достаточное условие экстремума.
- •Вывести уравнение касательной и нормали к плоской кривой.
- •Билет №24. Доказать теорему Бернулли-Лопиталя для предела отношения двух бесконечно малых функций.
- •Вывести формулу для производной частного от деления двух функций.
- •Билет №25. Доказать первое достаточное условие экстремума функции.
- •Сформулировать определение функции, непрерывной на отрезке. Свойства функций, непрерывных на отрезке.
- •Билет №26. Доказать теоремы Ролля и Ферма.
- •1. Определена и непрерывна на отрезке .
- •2. Дифференцируема на интервале .
- •3. И на концах отрезка принимает одинаковые значения.
- •Второе достаточное условие существования точки перегиба.
- •Определение б.Б. Функций. Теорема об их связи с б.М. Функциями.
- •Билет №28. Доказать достаточное условие выпуклости графика функции.
Билет №1. Доказать теорему Ролля.
Пусть дана функция
![]() .
.
Определена и непрерывна на отрезке
 .
.Дифференцируема на интервале
 .
.И на концах отрезка принимает одинаковые значения.
 .
.
Тогда найдется, по крайней мере, 1
![]()
![]() ,
принадлежащая интервалу
,
принадлежащая интервалу
![]() .
.
Доказательство: Т.к. функция
![]() непрерывна на отрезке
,
то согласно 2 теореме Вейерштрасса она
достигает своего минимального и
максимального значения.
непрерывна на отрезке
,
то согласно 2 теореме Вейерштрасса она
достигает своего минимального и
максимального значения.
![]() ,
,
![]() ,
,
![]() ,
.
,
.
Случаи:
 ,
- любое из интервала
,
- любое из интервала
 в силу 3-го условия теоремы, одно из
значений минимального или максимального
достигается функцией во внутренней
точке интервала
.
в силу 3-го условия теоремы, одно из
значений минимального или максимального
достигается функцией во внутренней
точке интервала
.
Согласно второму условию теоремы Ролля,
функция дифференцируема на интервале
в любой точке, то по теореме Ферма
существует
![]() .
.
Доказать теорему о предельном переходе в неравенстве.
Пусть
![]() при
при
![]() имеет конечный предел А1,
имеет конечный предел А1,
![]() при
имеет конечный предел А2, и
существует
при
имеет конечный предел А2, и
существует
![]() :
:
![]() для
для
![]() ,
тогда
,
тогда
![]() .
.
Доказательство:
![]() ,
,
![]()
![]() ,
,
![]()
![]()
![]()
![]()
Пусть
![]()
Это неравенство выполняется для любого
![]() ,
,
![]() отсюда
отсюда
Билет №2.
Доказать теорему Лагранжа.
Пусть функция
![]() .
.
Определена и непрерывна на отрезке .
Дифференцируема на интервале .
Тогда существует
из интервала
![]() .
.
Доказательство: Рассмотрим вспомогательную
функцию
![]() ,
где
,
где
![]() - константа.
- константа.

Она непрерывна на
дифференцируема на .
Все условия теоремы Ролля выполняются
![]() существует
из
существует
из
![]()
![]()
Формула Маклорена
для
![]() с остаточным членом в форме Пеано.
с остаточным членом в форме Пеано.
![]() ,
где
,
где
1) Пеано
2)
![]() где
где
![]() - Лагранж
- Лагранж
3)
![]() - Коши
- Коши
,
![]() ,
,
![]() ,
,
![]()
![]() ,
т.к. sin x -
нечет., то вып. усл.:
,
т.к. sin x -
нечет., то вып. усл.:![]()
Билет №3.
Формула Маклорена
для
![]() с остаточным членом в форме Пеано.
с остаточным членом в форме Пеано.
, где
1) Пеано
2) где - Лагранж
3) - Коши
![]() ,
,
![]() ,
,
![]() ;
;
![]()
Сравнение на бесконечности роста показательной, степенной и логарифмических функций.
1)![]()
![]() ,
где s>0, x>0;
,
где s>0, x>0;
![]() .
.
![]()
2)
![]() ;
;
![]() ;
;
 =
=![]() ;
;
![]() .
.
3)
![]() (по транзитивности)
(по транзитивности)
![]()
Билет №4.
Доказать первое достаточное условие экстремума функции.
Пусть функция определена и дифференцируема в окрестности точки С. Для того, чтобы точка С являлась точкой локального экстремума, достаточно чтобы при переходе значений аргумента через точку С производная функции меняла знак с “+” на “-” – локальный максимум, с “-” на “+” – локальный минимум.
Доказательство: Рассмотрим точку X из указанной окрестности, тогда:
на
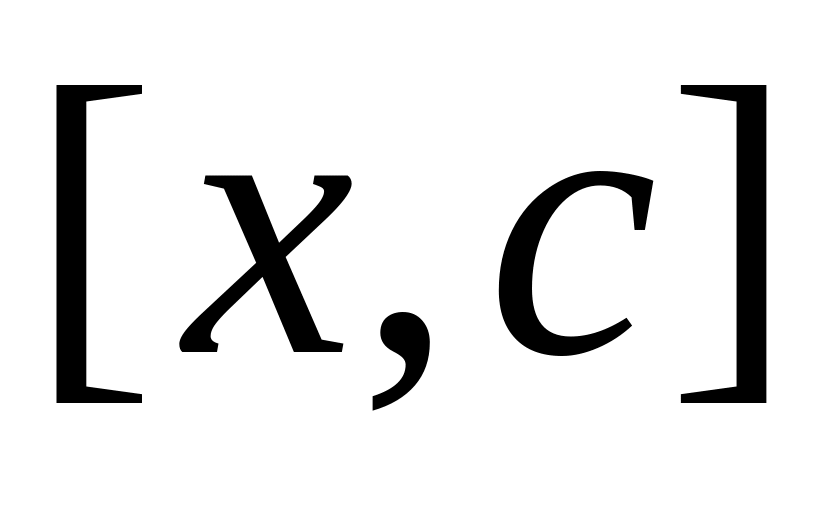 - непрерывна.
- непрерывна.на
 - дифференцируема.
- дифференцируема.
По т. Лагранжа
![]() ,
где
,
где
![]() ,
т.к.
,
т.к.
![]() ,
то
,
то
![]()
на
![]() :
:
![]() где
где
![]() ,
,
![]()
Доказать теорему о связи функции, её предела и бесконечно малой.
Для того, чтобы функция
,
определённая в
имела конечный предел при
,
необходимо и достаточно чтобы эту
функцию можно было представить в виде
суммы предела и б.м.ф. при
(![]() ,
где
,
где
![]() - б.м.ф. при
).
- б.м.ф. при
).
Доказательство: I Необходимость:
Дано:
![]()
Доказать:
![]() ,
где
- б.м.ф. при
.
,
где
- б.м.ф. при
.
![]()
Пусть
![]() по определению б.м.ф
по определению б.м.ф
![]() - б.м.ф. при
.
- б.м.ф. при
.
![]()
II Достаточность:
Дано: , где - б.м.ф. при .
Доказать:
![]()
Билет №5. Доказать второе достаточное условие экстремума.
Пусть функция
определена и имеет в окрестности точки
с производную до n-го
порядка включительно, причем в самой
точке с все производные до (n-1)-го
порядка включительно равны 0, а n-ая
производная в точке С отлична от нуля.
Если n – четное, тогда С
– точка локального экстремума, в
частности, если
![]() ,
то x=c –
локальный минимум, если
,
то x=c –
локальный минимум, если
![]() ,
то x=c –
локальный максимум.
,
то x=c –
локальный максимум.
Доказательство: Запишем формулу Тейлора с остаточным членом в форме Пеано с центром в точке С.
 ,
где
,
где
![]() -
б.м.ф. при
-
б.м.ф. при
![]() .
Пусть n – четное, тогда
.
Пусть n – четное, тогда
![]() не меняет знак при переходе через С.
не меняет знак при переходе через С.
![]()
![]() в которой функция сохраняет знак своего
предела.
в которой функция сохраняет знак своего
предела.
![]() ,
,
![]() .
.
![]() .
.
![]() ,
если
,
если
![]() -
точка локального экстремума.
-
точка локального экстремума.
