2.2. Обходы в графах
В процессе проектирования зачастую требуется найти оптимальную последовательность действий по одиночной либо парной обработке объектов. Для этого в графовых мо-делях систем необходимо строить обходы вершин либо рё-бер.
Определение. Простой цикл, содержащий все верши-ны графа, называется гамильтоновым.
Определение. Гамильтоновой цепью называется прос-тая цепь, содержащая все вершины графа.
Очевидно, если граф имеет гамильтонов цикл, то он имеет и гамильтонову цепь, обратное верно не всегда.
Пример 1. Определить, существует ли гамильтонов цикл и гамильтонова цепь в показанном на Рис.4.20 графе G = (V, X), V = (1, 2, 3, 4, 5, 6), X = ((1, 2), (1, 3), (1 ,4), (2, 3), (3, 4), (4, 5), (4, 6), (5, 6)).
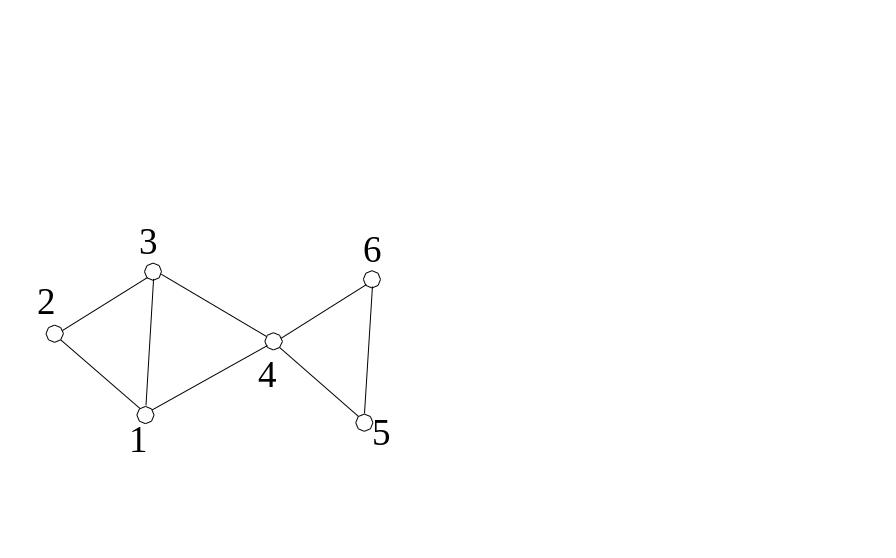
Рис.4.20
Решение.
1. Рассмотрим построение гамильтонова цикла. Допустим, он существует. В качестве начальной может быть принята
269
любая вершина, например, V1 . При переходе от V1 к V5 и обратно вершина V4 должна быть пройдена как минимум 2 раза. Поэтому любой цикл, содержащий все вершины графа, не будет простым, ( а , следовательно, и гамильтоновым ).
2. Цепь V1V2V3V4V5V6 является гамильтоновой.
Ответ: гамильтонова цепь в данном графе G существует, а гамильтонов цикл – нет.
Определение. Эйлеровым циклом называется цикл, содержащий все рёбра графа.
Определение. Эйлеровой цепью называется цепь, со-держащая все рёбра графа.
Критерий существования эйлерова цикла в графе име-ет следующий вид.
Теорема. Эйлеровым циклом обладают все связные графы, у которых степени всех вершин чётны.
Пример 2. Определить, существует ли эйлеров цикл и эйлерова цепь в графе G =(V,X) из предыдущего Примера 1.
Решение.
1. По вышеприведенной Теореме эйлеров цикл не сущест-вует, поскольку существуют вершины с нечётными сте-пенями вершин ( V1 и V3 ).
2.Цепь (V1 V2) (V2 V3) (V3 V1) (V1 V4) (V4 V5) (V5 V6) (V6 V4) (V4 V3) является эйлеровой.
Ответ: эйлерова цепь в графе G существует, цикл – нет.
Задачи.
1. Выяснить, существуют ли гамильтоновы цепи и циклы в графах Tn , Wn,k ,Kn ,Kn,m , Bn.
2. Доказать, что граф с висячей вершиной не имеет гамиль-тонова цикла.
3. Привести пример графа, имеющего гамильтонову цепь, но не имеюшего гамильтонова цикла.
4. Доказать, что показанный ниже граф не имеет гамильто-нова цикла:
270
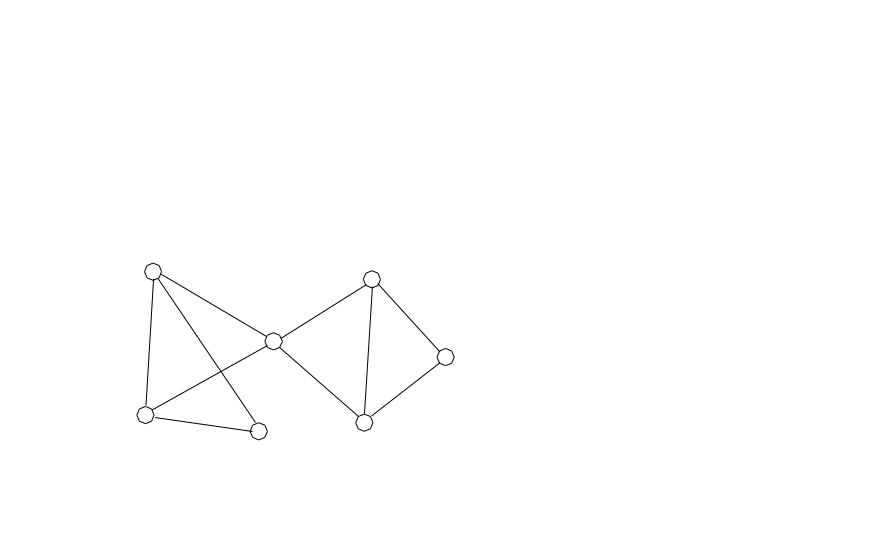
Рис.4.21
5. Будет ли любой связный граф иметь гамильтонову цепь?
6. Доказать, что эйлеровой цепью обладает всякий связный граф, у которого количество вершин нечётной степени не больше 2.
7. Построить эйлеров цикл в графе
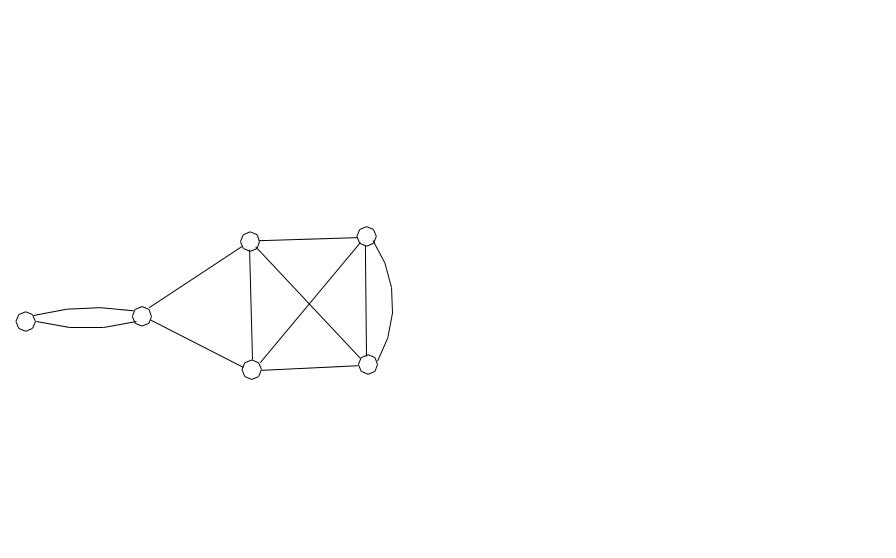
Рис.4.22
2. 3. Раскраски графов
В ряде случаев при разработке систем требуется при-своить её элементам (либо связям) некоторые свойства та-ким образом, чтобы объекты с одинаковыми свойствами не взаимодействовали непосредственно между собой. В гра-фовых моделях приписывание свойств вершинам или рёб-рам условно называется раскраской, т.е. полагается, что каждому свойству соответствует свой определённый цвет.
271
Определение. Если смежные вершины (рёбра) графа раскрашены в различающиеся цвета, то соответствующая вершинная (рёберная) раскраска называется правильной.
По умолчанию под раскраской графа подразумевается вершинная раскраска.
Определение. Наименьшее число цветов, требуемое для правильной раскраски (рёберной раскраски) графа G, называется хроматическим (рёберным хроматическим) чис-лом графа G и обозначается (G) ( (G) ).
Рассмотрим наиболее употребительные оценки для хроматических чисел графов.
Утверждение 1. (G) n, где n – число вершин.
Доказательство. Справедливость Утверждения 1 следует из того, что раскраска вершин, при которой все они имеют различные цвета, является правильной. Оценка достигается на полных графах Кn , поскольку у них все вершины смеж-ны.
Утверждение 2. Пусть граф G содержит полный под-граф Кl с l вершинами. Тогда (G) l.
Доказательство. Из ( Кl) = l следует: (G) ( Кl) = l.
Утверждение 3. (G) m, где m – число рёбер.
При раскраске всех рёбер различными цветами усло-вие правильности раскраски автоматически выполняется. Данная оценка достигается на звёздах с m лучами , посколь-ку у них все рёбра смежны.
Утверждение 4. ( G ) max d( v ), где max d( v ) – максимальная степень вершин графа G.
Рассмотрим звезду S с центром в вершине с макси-мальной степенью и лучами – рёбрами, исходящими из vi . Справедливость утверждения следует из очевидных соотно-шений: (G) (S) = d(vi)= max d(v).
Пример 1. Найти хроматические числа (G) , (G) и
272
построить правильные раскраски с минимальными числами используемых цветов показанного на Рис.4.22 графа G = (V,X), V = (1,2,3,4,5), X = ((1,2), (1,5), (2,3), (2,5), (3,4), (3,5), (4,5)).
Решение. Из структуры графа следует: n=5, m=7,max d(v)= d(V5) =4. Максимальное число вершин в полных подграфах l=3 (например, в подграфе, образованном вершинами V1 ,V2, V5 и рёбрами между ними).
1.Рассмотрим вершинную раскраску. Из Утверждений 1,2 следует, что l(G) n, 3 (G) 5. Полученная оценка по-казывает, что минимальное количество цветов, необхо-димых для правильной раскраски, лежит в интервале от 3 до 5. Поскольку правильная раскраска вершин тремя цветами (I,II,III) существует (она показана на изображении графа), то отсюда следует, что (G)=3.
2.Рассмотрим рёберную раскраску. Из Утверждений 3,4 сле-дует, что max d(v) (G) m. В данном примере: 4 (G) 7. Так как правильную рёберную раскраску графа можно построить четырьмя цветами (на рисунке цвета рёбер обо-значены I*,II*,III*,IV*), то отсюда следует: (G)=4.
Рис.4.23
273
В ряде случаев построение правильных рёберных рас-красок проще производить с использованием матрицы смежности графа. В ней ребра вместо единиц отмечаются числовыми обозначениями присвоенных им цветов. Напри-мер, для графа на Рис.4.23 соответствующая матрица смеж-ности имеет вид:
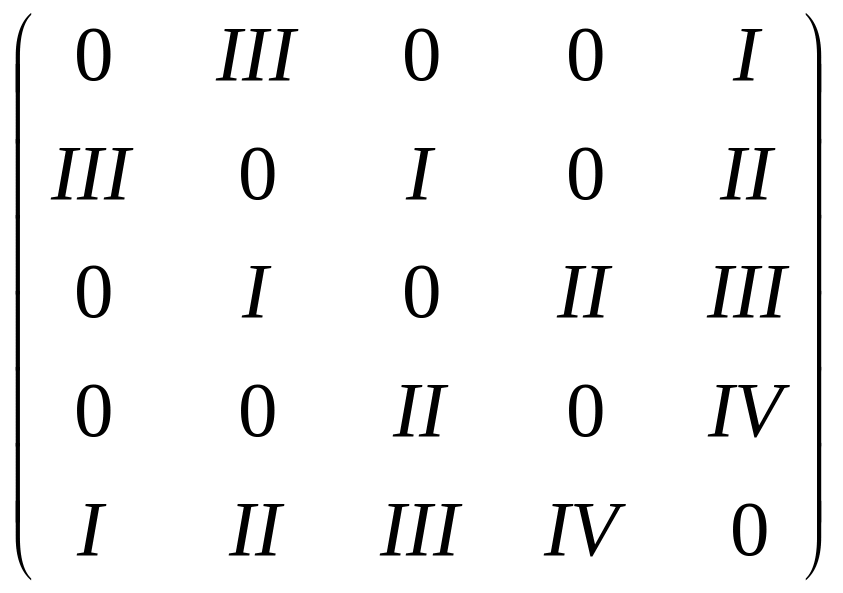
Матрица смежности, соответствующая правильной реберной раскраске, обладает следующим свойством – в каждой строке и каждом столбце не может больше одного раза встречаться обозначение одного и того же цвета.
Задачи.
1. Доказать, что (К n,n) = 2.
2. Доказать, что (T) = 2 при n>1 (например, индукцией по числу вершин).
3. Доказать, что (Кn,n) = n (например, с использованием матрицы смежности).
4. Доказать, что у деревьев (T) = max d(v), где d(v) – степени вершин (например, индукцией по числу вершин).
5. Доказать, что (К n) = n-1 (при n – чётном), (К n) = n (при n – нечётном) - например, с использованием матрицы смежности.
6.Найти хроматические числа (G) и (G) и построить пра-вильные раскраски с минимальными числами цветов гра-фов :
а) на Рис.4.5, б) на Рис.4.21, в) на Рис.4.22.
274