
Исследование на плоскости уравнения второй степени
Рассмотрим
уравнение:
![]()
где среди коэффициентов есть отличные от нуля, т.е. (7.9) – уравнение второй степени относительно и .
Возьмем
на плоскости две прямоугольные системы
координат:
,
которую будем называть старой, и новую,
полученную из
поворотом ее вокруг начала координат
на угол
,
![]() .
.
Старые
координаты
выражаются через новые координаты
![]() по формулам:
по формулам:
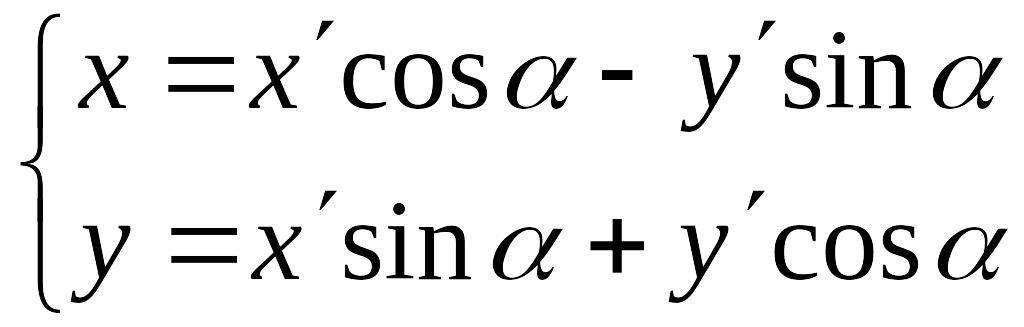
Подставив
выражения для
и
в уравнение (8), получим:
![]()
Это уравнение в системе координат задает ту же линию, что и уравнение (7. 9) в системе .
Если
в уравнении (7.9)
![]() ,
то за счет выбора угла
в (7.10) можно добиться того, что
,
то за счет выбора угла
в (7.10) можно добиться того, что
![]() .
Для этого угол
надо взять таким, чтобы
.
Для этого угол
надо взять таким, чтобы
![]() .
Поэтому будем считать
,
тогда уравнение (7.11) примет вид:
.
Поэтому будем считать
,
тогда уравнение (7.11) примет вид:
![]()
Преобразуя
это уравнение и применяя параллельный
перенос координатных осей, придем к
уравнению:
![]()
Параллельный перенос и поворот системы координат на плоскости.
Мы
рассматриваем прямоугольную декартову
систему координат. При параллельном
переносе системы координат сохраняется
направление координатных осей, но
меняется положение начала координат
.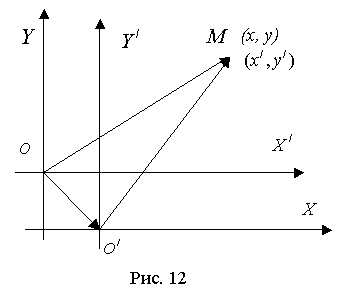
Пусть Оху - "старая" система координат, а О'х'у' - "новая" система координат. Пусть произвольная точка Мимеет координаты (х, у) в "старой" системе, и она же имеет координаты (х', y')в новой системе, кроме того, пусть новое начало O' имеет координаты (а, b) в "старой" системе (рис. 12).
Тогда![]()
Т.к. при параллельном переносе осей координат базис не меняется, то при сложении векторов можно складывать их координаты.
Следовательно,
имеем![]()
Формулы (42) есть формулы перехода, связывающие "старые" и "новые" координаты.
Приведение общего уравнения второго порядка к каноническому виду.
Укажем,
как можно с помощью преобразований
координат, рассмотренных в предыдущем
параграфе, привести общее уравнение
кривой второго порядка![]() к
каноническим уравнениям эллипса,
гиперболы или параболы, или к случаям
их выражения.С
помощью поворота осей координат на
некоторый угол α всегда можно избавиться
от члена с произведением координат.
Действительно, подставляя в (47) вместо
x и y их выражения по формуле (43), получим
новое уравнение
к
каноническим уравнениям эллипса,
гиперболы или параболы, или к случаям
их выражения.С
помощью поворота осей координат на
некоторый угол α всегда можно избавиться
от члена с произведением координат.
Действительно, подставляя в (47) вместо
x и y их выражения по формуле (43), получим
новое уравнение![]() коэффициент
которого a'12 будет
равен
коэффициент
которого a'12 будет
равен![]()
Приравнивая
коэффициент a'12 к
нулю, получим тригонометрическое
уравнение![]() Отсюда
получаем
Отсюда
получаем![]() Далее,
по формулам тригонометрии, получаем
нужные нам значения для sin α и cos α
:
Далее,
по формулам тригонометрии, получаем
нужные нам значения для sin α и cos α
:![]()
![]()
![]() Следовательно,
уравнение кривой в новых координатах
O'x'y' примет вид:
Следовательно,
уравнение кривой в новых координатах
O'x'y' примет вид:![]() Если
в уравнении (50)
Если
в уравнении (50) ![]() ,
то говорят, что это уравнение определяет
линию эллиптического типа;
если
же
,
то говорят, что это уравнение определяет
линию эллиптического типа;
если
же ![]() ,
то говорят, что уравнение определяет
линию гиперболического типа и, если
один из коэффициентов a'11 или
a'22 равен
нулю, то уравнение (50) определяет линию
параболического типа. Далее с помощью
параллельного переноса системы координат
O'x'y' уравнение (50) всегда можно привести
к виду:
,
то говорят, что уравнение определяет
линию гиперболического типа и, если
один из коэффициентов a'11 или
a'22 равен
нулю, то уравнение (50) определяет линию
параболического типа. Далее с помощью
параллельного переноса системы координат
O'x'y' уравнение (50) всегда можно привести
к виду:![]() т.е.
фактически к каноническому виду.
т.е.
фактически к каноническому виду.
Из
уравнения (51) следует, что мы имеем либо
эллипс (если a'11 и
a'22 одного
знака, а a"0противоположного),
либо
мнимое место точек (если a'11,
a'22,
a"0 имеют
один знак),
либо
одну точку (если a'11 и
a'22 имеют
один знак, а a"0 =
0),
либо
гиперболу (если a'11 и
a'22 разных
знаков и a"0 ≠
0),
либо
две пересекающие прямые (если a'11 и
a'22 разных
знаков и a"0 =
0). Если же в уравнении (50) один из
коэффициентов a'11 и
a'22 ,
например, a'22 обращается
в нуль, то это уравнение с помощью
переноса осей приведется к каноническому
уравнению параболы ![]() при
a'22 ≠
0 или к виду
при
a'22 ≠
0 или к виду ![]() при
a'22 =
0, что дает или две параллельные прямые,
или мнимое место точек.
при
a'22 =
0, что дает или две параллельные прямые,
или мнимое место точек.
Отсюда следует, что всякая кривая 2-го порядка есть либо эллипс, либо гипербола, либо парабола, либо представляет собой их "вырождение".
