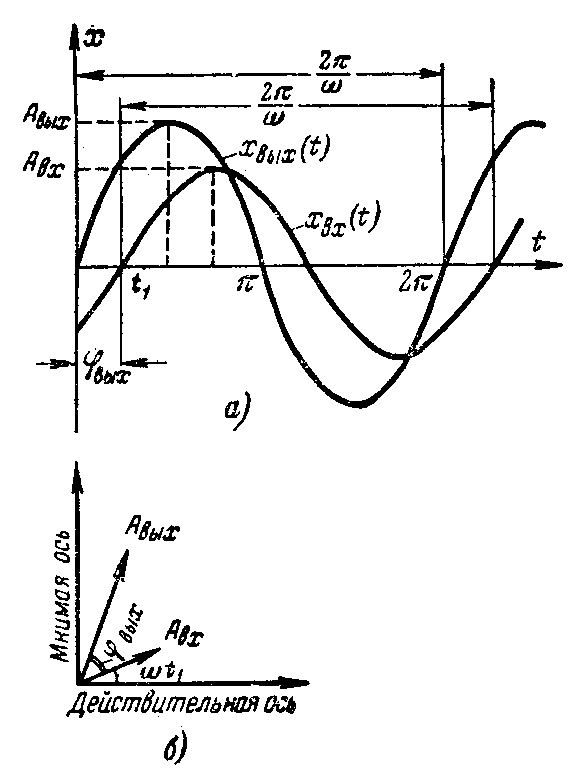
20 Частотные характеристики. Комплексная плоскость.

Если на вход системы или звена подавать синусоидальные (гармонические) колебания с постоянными амплитудой и частотой , то после затухания переходных процессов на выходе также возникают периодические колебания с той же частотой, но с другой амплитудой и сдвинутые по фазе отн-но входных колебаний (рис. 3.8).

На комплексной плоскости входная величина для каждого момента времени, например , определяется вектором , проведенным из начала координат под углом .

Как видно из рис. 3.8, б, действительная часть гармонической входной величины, представленная в комплексной форме, равна как проекция вектора на ось абсцисс, а мнимая как проекция на ось ординат.

Обозначив значения комплексной входной величины для различных значений времени в виде , получим выражение для входной величины в комплексной тригонометрической форме:

(3.1)

Так как согласно формуле Эйлера: , то входная величина в комплексной показательной форме запишется как

Аналогичным образом выходная величина в комплексной показательной форме имеет вид:

. (3.2)

Если начальная фаза входной величины не равна нулю, то в общем случае имеем:

, (3.3)

Тогда

. (3.4)

Отношение выходной величины системы к входной величине, выраженное в комплексной форме, называется амплитудно-фазовой характеристикой АФХ системы.

Отношение амплитуд является модулем АФХ, а разность фаз является ее фазой. Амплитудно-фазовая хар-ка системы не зависит от времени. В этом ее принципиальное отличие от временной характеристики. Если временная хар-ка опр-ет поведение системы в переходном процессе, то АФХ выражает зав-ть параметров установившихся выходных колебаний от тех же параметров входных колебаний при различных частотах.

Однако, несмотря на то, что АФХ отображает только установившиеся процессы в системе, она в полной мере определяет также ее динамические свойства подобно временной хар-ке и дифференциальным ур-ям.

Так как

;

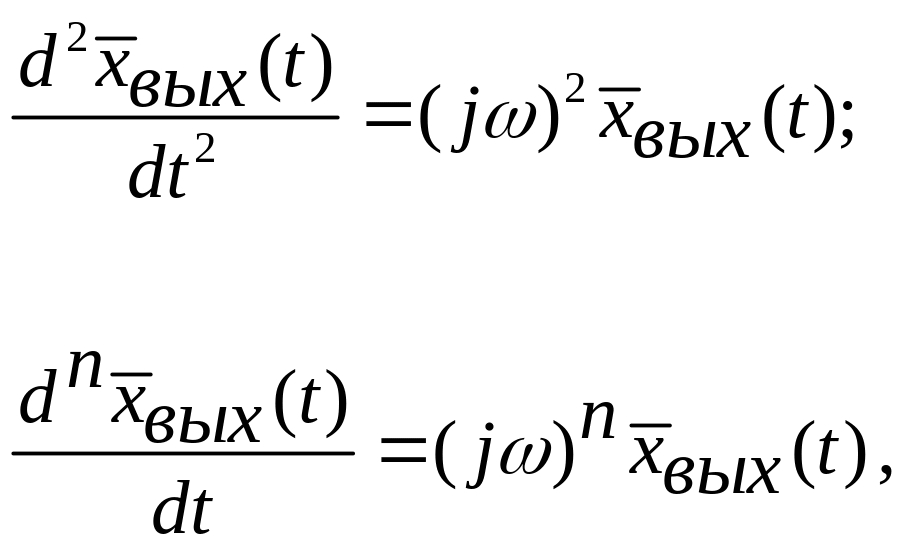
то при подстановке этих выражений для производных в дифференциальное уравнение для случая воздействия на нее гармонических колебаний получим:

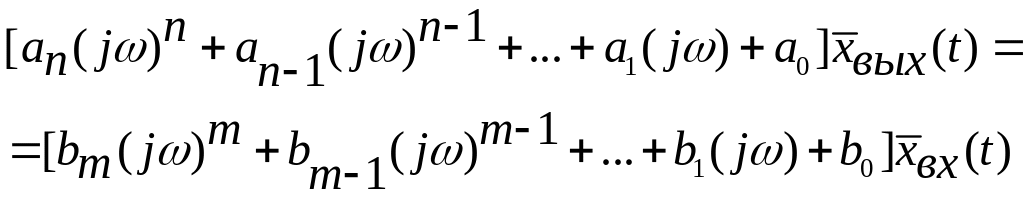(3.5)

Из выражения (3.5) определяем АФХ системы:

(3.6)

При сравнении выражений (3.6) и (2.5) видно, для получения АФХ достаточно в передаточной ф-ии звена или системы заменить переменную .

Обозначив в соотношении (3.4) и , получим: . (3.7)

Зависимость отношения амплитуд выходных и входных колебаний от частоты называется амплитудно-частотной характеристикой (АЧХ).

. (3.8)

Амплитудно-частотная характеристика является модулем АФХ

. (3.9)

Зависимость разности фаз выходных и входных колебаний от частоты называется фазо-частотной характеристикой (ФЧХ) системы

. (3.10)

Фазо-частотная характеристика является аргументом АФХ системы.

Поскольку

- …;

-…,

то, отделив полиномиальные составляющие действительной и мнимой частей, получим:

;

, где - …- действительная составляющая полинома ; -…- мнимая составляющая полинома ; -…- действительная составляющая полинома ; -…- мнимая составляющая полинома .

С учетом этих зависимостей АЧХ системы выразится следующим образом

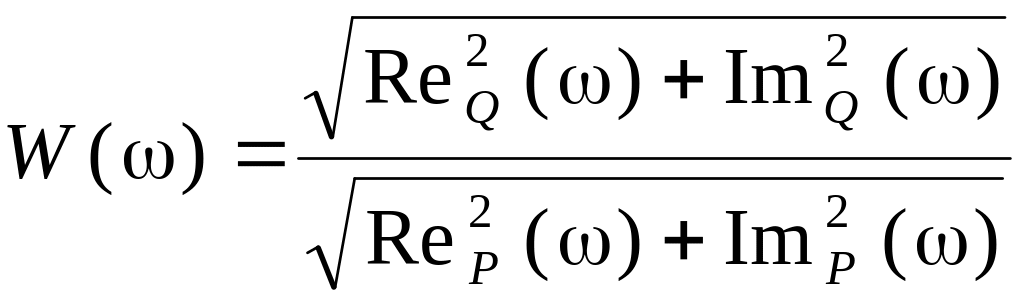. (3.11)

Амплитудно-фазовая характеристика

. (3.12)

Умножив числитель и знаменатель этой дроби на сопряженный множитель , получим:

.

Обозначив

; (3.13)

, (3.14)

имеем:

. (3.15)

Величина называется вещественной частотной характеристикой системы.

Величина называется мнимой частотной характеристикой системы.

Таким образом, получаем всего пять частотных характеристик:

• амплитудно-фазовая ;

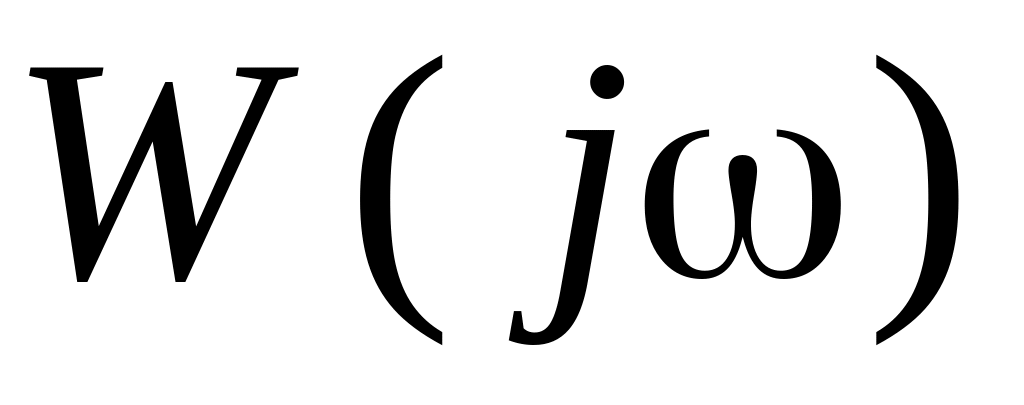• амплитудно-частотная (модуль АФХ) ;

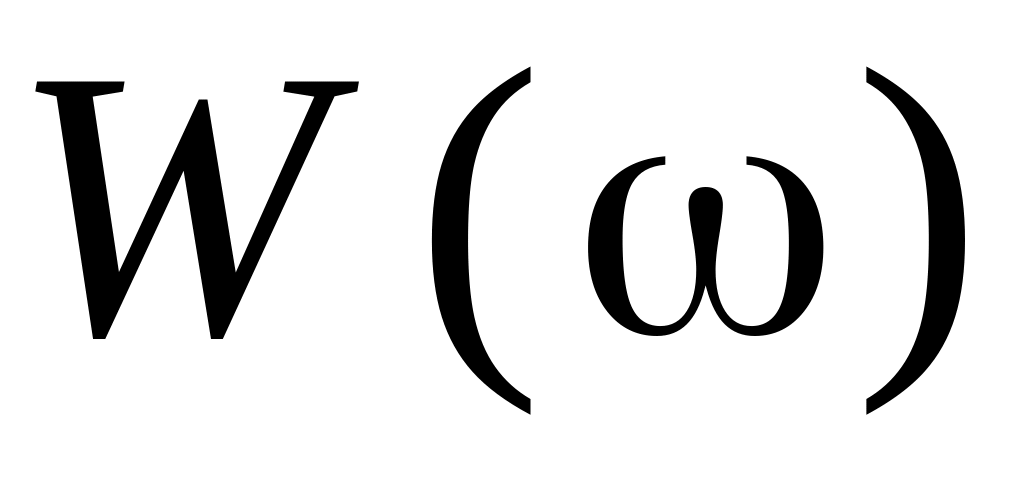• фазо-частотная (аргумент АФХ) ;

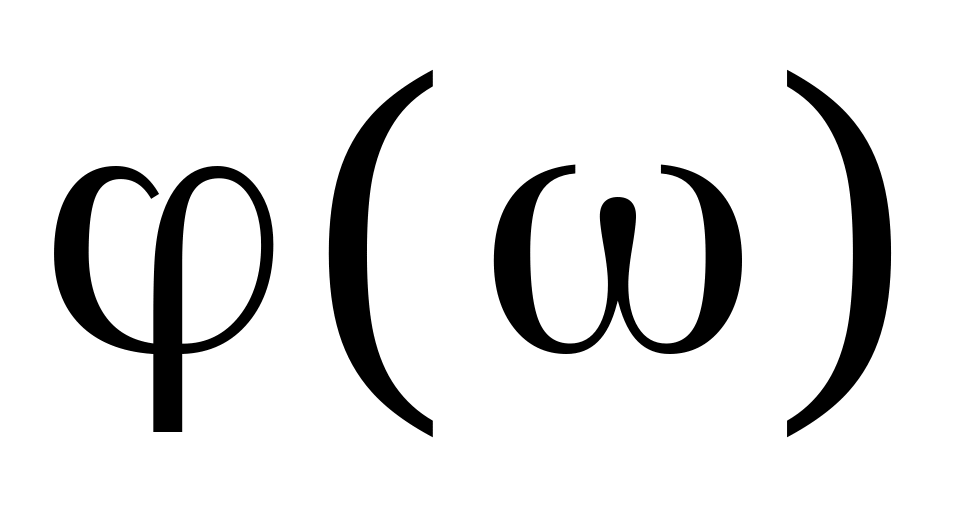• мнимая частотная ;

• вещественная (действительная) частотная .

Между этими характеристиками, кроме вышеприведенных зависимостей, имеются следующие очевидные связи:

; (3.16)

. (3.17)

Для инженерных расчетов находит широкое применение графическое изображение АФХ на комплексной плоскости в координатах . Такое графическое изображение называется годографом.

Годограф – это геометрическое место точек концов векторов, которое прочерчивает функция при получении приращения переменной в некотором заданном диапазоне частот .

Из выражения (3.13) следует, что вещественная частотная характеристика является четной функцией частоты, так как входит как в числитель, так и в знаменатель только в четных степенях ( и т.д.), .

Из выражения (3.14) видно, мнимая частотная характеристика является нечетной функцией частоты, т.е. .

Таким образом, точки АФХ, соответствующие значениям и , имеют одну и туже абсциссу и равные по модулю, но разные по знаку ординаты .

На АФХ наносятся частотные отметки и стрелками указывается направление возрастания частоты (рис. 3.9).

Для инженерных расчетов получили широкое распространение частотные характеристики, построенные в логарифмическом масштабе в виде в виде кусочно-непрерывных (асимптотических) функций. Графики и удобно выражать в логарифмическом масштабе, откладывая по оси абсцисс десятичный логарифм частоты, единица которого соответствует изменению частоты в десять раз. В этом случае говорят, что частота измеряется в декадах по отношению к некоторой заданной частоте, соответствующей началу отсчета.

Модуль коэффициента передачи при этом измеряется в децибелах (дБ). , или .

Зависимость называется логарифмической амплитудно-частотной характеристикой (ЛАЧХ), а – логарифмической фазочастотной характеристикой (ЛФЧХ).

Характеристика

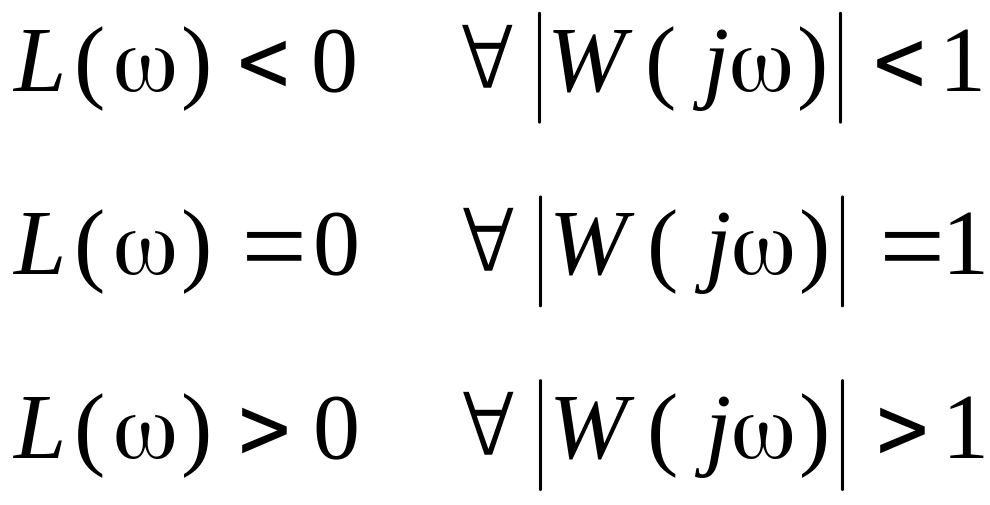
Так как при в реальных системах (степень числителя дробно-рациональной функции меньше степени знаменателя) , то .

Для построения ЛАХ и ЛФХ используется стандартная сетка – полулогарифмический масштаб (рис. 3.11).

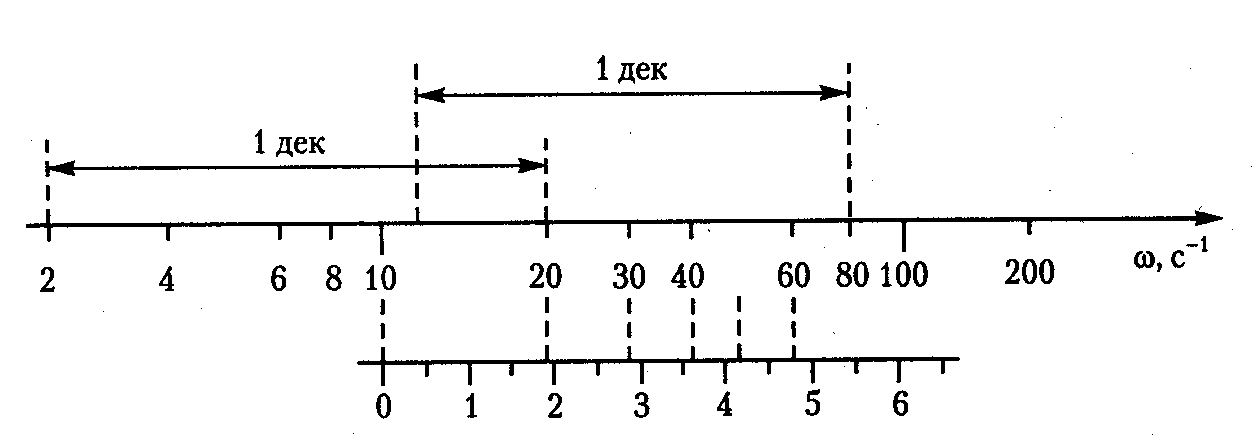
По оси абсцисс откладывается угловая частота в логарифмическом масштабе, т.е. наносятся отметки, соответствующие , а около отметок записывают само значение частоты в рад/с.