
- •2.Случайные события и их классификация.
- •11.Понятие дискретной случайной величины ее закона распределение. Многоугольник распределения. Примеры.
- •12.Функция распределения случ. Величины и ее св-ва. График ф-ции распределения дискретной случайной величины.
- •31. Неравенство Чебышева
- •32. Теорема Чебышева и её следствия
- •33. Теорема Бернулли. Значение збч
31. Неравенство Чебышева
Вероятность
того, что отклонение случ. величины Х
от ее мат. ожидания по абсол. величине
< положит. числа
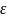 не меньше, чем
не меньше, чем
 :
:
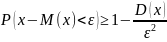 .
.
Док-во:

M(Y)=D(X)
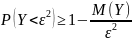 .
.
 .
.
 .
.
 .
.
Неравенство имеет для практики огр. значение, поскольку часто дает грубую или иногда тривиальную оценку. В теории исп-ся для вывода Т. Чебышева.
32. Теорема Чебышева и её следствия
Т.
При
неограниченном увеличении числа n
попарнонезавис. случ. величин имеющих
M(X)
и равномерноогр. D(X),
их ср. арифмет.
 стремится по вер-сти к ср. арифмет. их
матем. ожиданий.
стремится по вер-сти к ср. арифмет. их
матем. ожиданий.

Следствия:
Пусть случ. величины
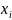 имеют равные мат. Ожидания
имеют равные мат. Ожидания
 (i=
1, 2, …n)
и равномерногр.
(i=
1, 2, …n)
и равномерногр.
 .
Тогда ср. арифмет.
.
Тогда ср. арифмет.
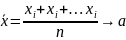
Если
случ. величины
попарно независ. И одинаково распред-ны,
то ср. арифмет.
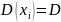 ,
,

33. Теорема Бернулли. Значение збч
Если
вер. Р – наступление соб. А в каждом из
n
повторнонезавис. испытаний постоянно,
то при
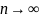 относит. частота
относит. частота
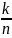 появление соб. А стремится к Р при
.
К – число наступления соб. А в n
повт. независ. испытаний как сумму
попарнонезавис.
появление соб. А стремится к Р при
.
К – число наступления соб. А в n
повт. независ. испытаний как сумму
попарнонезавис.
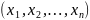 ,
где
имеет распределение
,
где
имеет распределение
-
x
0
1
p
p
q
0 – соб. А ненаступило, 1 – наступило
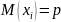 ,
,
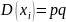
При подстановке получаем
 ,
,
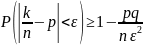 ,
при
,
при

Если
,
то правая часть стремится к 1, но вер-сть
не может быть > 1, значит
 ,
что треб-ость доказать.
,
что треб-ость доказать.
ЗначениеЗБЧ:
1 в физике-пос-во давления газа
2 в статистике-основа выбора метода
3 в страховании-основанно на устойчивых таблицах смертности
34
Понятие о центральной предельной
теореме (ЦПТ) и ее следствиях.существуют
несколько форм ЦПТ. В них утверждается
факт, что если случ.велич. х является
результатом суммарного воздействия
многих случайных величин, влияние
каждой из которых на сумму ничтожно
мало, то эта суммарная величина имеет
нормальный закон растпеделения.
Центральная
предельная теорема (ЦПТ)
( в формулировке Ляпунова А.М. для
одинаково распределенных СВ).
Если случ.вел-ны
 имеют
конечные мат.ожидания
имеют
конечные мат.ожидания
 и дисперсии
и дисперсии
 и абсолютные центральные моменты
и абсолютные центральные моменты
 где
где
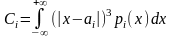 и выполняется усл-е Ляпунова
и выполняется усл-е Ляпунова
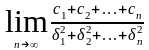 =0, то случ.вел. Х=
=0, то случ.вел. Х= с достаточной степенью точности
распределена по норм-му закону с
параметрами
с достаточной степенью точности
распределена по норм-му закону с
параметрами
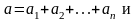
 .
.
Если
случ.вел-ны
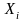 распределены точно по норм-ну закону,
то их суммы
распределены точно по норм-ну закону,
то их суммы
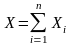 имеют
точно норм-е распределение.
имеют
точно норм-е распределение.
Если все величины распределены одинаково,то усл-е Ляпунова выполняется автоматически и значит сумма случайных величин с достаточной степению точности имеет норм-е распр-е.
Примеры из практики:1)ошибки измерений:случ.вел.кот распределена по норм.закону.2)нагрузка потребительских сил.3)биометрические показатели.
35Предмет и задачи мат статистики, ген и выборочная совокупности, способ отбора.Мат стат-раздел математики, изучающий методы отбора, систематизации и обработки результатов наблюдений, массовых случ явлений с целью выявления существующих закономерностей. Она возникла как наука в нач 17в. В работах Галелея, кот. Исследовал ошибки физич. измерений, рассматривая их как случ-е явления. Затем создается теория страхования,основанная на анализе таких массовых случ. явлений как рождаемость и смертность.19в – матем.стат.как отдельная наука(Кетле,Гальтон,Пирсон)
Задачи:1-указание способов сбора и группировки стат сведений (описательная статистика) 2-разработка методов анализа стат данных а) оценка вероятности события б)функции распределения в) зависимость случ величины от других величин г) проверка стат гипотез. Ген сов-ть – сов-ть объектов, все элементы кот подлежат изучению; м.б. конечной/бесконечной. Выборочная сов-ть часть объектов ген сов-ти используемая для исследования. Способы отбора: 1)простой случайный бесповторный, когда кажд элемент, случайно отобранный исследователем, не возвращается в ген сов-ть 2)простой случайный повторный отбор, когда элемнт возвращается в ген сов-ть. Выборка должна быть репрезентативной. т.е. правильно отражать пропорции генер-й сов-ти. Для этого каждый элемент ген.совокупности должен иметь одинак. вер-ть попасть в выборку.
36
Построение дискретного вариационного
ряда.
Эмпирическая ф-ия распределения.Случ.вел.
Х носит дискретный хар-р или кол-во
признака Х. Дан ряд чисел. Вначале он
ранжируется, т.е. располагаются по
возрастанию. Различные элементы выборки
наз-ся вариациями. Частотой варианта
наз-ся число
 ,
показывающее скоко раз эта вар-та
встречается в выборке. Частостью
(относит-ой частотой) наз-ся число
,
показывающее скоко раз эта вар-та
встречается в выборке. Частостью
(относит-ой частотой) наз-ся число
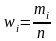 .
Частости и частоты наз-ся весами.
Накопленной частотой наз-ся число n
= кол-ву вариант знач-е кот меньше х.
.
Частости и частоты наз-ся весами.
Накопленной частотой наз-ся число n
= кол-ву вариант знач-е кот меньше х.
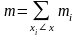 аналогично опр-ся накопленная частота.
.
Ряд вариант, расположенный в порядке
возраст-я вместе с соотв. весами наз.
стат. рядом частот или частостей.
аналогично опр-ся накопленная частота.
.
Ряд вариант, расположенный в порядке
возраст-я вместе с соотв. весами наз.
стат. рядом частот или частостей.
Для графического изображения ДВП используют: 1) точечную диаграмму(строится по координатам (хi;ni)). 2)полигон(соединить точки). 3) кумулята (ломанная, кот соединяет точки с координатами (хi;mхi) )(кумуляц-я кривая).
Эмпирической
ф-ей распр-я наз.
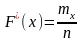 где
где
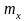 -
число вариант меньшее, чем х.
-
число вариант меньшее, чем х.
 {
св-ва:1)
{
св-ва:1)
 принадлежит [0;1]. 2) неубывающая. 3)
принадлежит [0;1]. 2) неубывающая. 3)
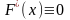 при
х
при
х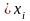 .
4)
.
4)
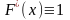 при х
при х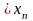 .
.
Простейшие
числ. хар-ки вариац. ряда: 1)R
– размах вар-ции Хмакс-Хмин. 2)М – мода,
имеет наибольшую частоту.3) Ме – медиана,
число, слева и справа от кот нах-ся
одинак. число вариант, может попадать/не
попадать в ряд.
если ДВР содержит
четн число вариант, то Ме= .
.
40.Оценка
парам-в генер.сов-ти.Пон.точеч.оценки
и её св-ва:несмещ-ть,состоят-ть,эффективность.
Выбор.хар-ка,использ-я
в кач-ве приближ-го знач.неизвестной
хар-ки наз её точеч.статист.оценкой.
Напр.,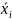 (выборочная)
оценка М(Х).
х—суммарный
балл в летней сессии. Оценка наз.точечной,
пот.что предст.собой число—точку на
числовой прямой. Слово «статистич-я»
означ.,что оценка рассчит.по результ-м
выборки(стат-ки). Тогда становится
понятно,что точеч.статист.оценка
явл.СВ,т.к.элементы выборки случ-е. Тогда
м.говорить о М(Х) и D(Х)
самой стат-ой оценки. Стат.оценка наз-ся
несмещённой,если её М(Х) равно оценив-му
интерв.парам-ру. Стат.оценка наз-ся
состоятельной,если она стремится по
вер-ти к оцениваемому парам-ру, т.е.с
повышением объёма выборки оценка и
чел.хар-ка отлич-ся сколь угодно мало.
Если есть неск-ко способ.получения
точеч.оценки,то эффект-й наз.та, кот.имеет
наим возможную дисперсию среди всех
оценок.
(выборочная)
оценка М(Х).
х—суммарный
балл в летней сессии. Оценка наз.точечной,
пот.что предст.собой число—точку на
числовой прямой. Слово «статистич-я»
означ.,что оценка рассчит.по результ-м
выборки(стат-ки). Тогда становится
понятно,что точеч.статист.оценка
явл.СВ,т.к.элементы выборки случ-е. Тогда
м.говорить о М(Х) и D(Х)
самой стат-ой оценки. Стат.оценка наз-ся
несмещённой,если её М(Х) равно оценив-му
интерв.парам-ру. Стат.оценка наз-ся
состоятельной,если она стремится по
вер-ти к оцениваемому парам-ру, т.е.с
повышением объёма выборки оценка и
чел.хар-ка отлич-ся сколь угодно мало.
Если есть неск-ко способ.получения
точеч.оценки,то эффект-й наз.та, кот.имеет
наим возможную дисперсию среди всех
оценок.
41.Точеч.оценки
математич.ожидания и дисперсии.Устойчивость
выборочных средних.Исправленная
выбороч.дисперсия. Теорема.Выборочная
ср.арифметич.явл.несмещённой оценкой
генер.ср.арифметич-й. М )=
)=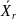 Пусть из генер.совок-ти,в кот.изм-ся
конечн.признак Х извлечена выборка
объёмом n.
Пусть из генер.совок-ти,в кот.изм-ся
конечн.признак Х извлечена выборка
объёмом n.
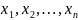 (конкрет.реализация
выборки) Вычислим ср.арифмет.:
(конкрет.реализация
выборки) Вычислим ср.арифмет.: .
Понятно,что вместо
м.быть любое значение из возможных
знач-й Х. То же самое для
.
Понятно,что вместо
м.быть любое значение из возможных
знач-й Х. То же самое для
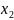 и т.д., поэтому
и т.д., поэтому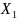 ,
,
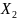 ,…,
,…,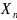 это
случ.величины,кот.распределены так же,
как и вся генер.совок-ть:М(
)=M(
)=…=M(
)=M(X)=
это
случ.величины,кот.распределены так же,
как и вся генер.совок-ть:М(
)=M(
)=…=M(
)=M(X)=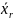 .
Т.к.СВ
.
Т.к.СВ
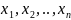 —независ-е,
то применяя св-во мат.ожид.выборочной
средней, получ:
М(
—независ-е,
то применяя св-во мат.ожид.выборочной
средней, получ:
М(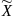 )=М(
)=
)=М(
)=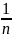 M(
M( )=
(M(
)=
(M(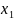 )+M(
)+…+M(
)+M(
)+…+M(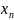 ))=
(M(X)+M(X)+…+M(X))=
))=
(M(X)+M(X)+…+M(X))=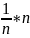 *M(X)=M(X).
В доказ-ве предполаг,что выборка
повторная. Замечание:из Т.Чебышева
след,что выборочная средняя явл.и
состоятельной оценкой ген.средней.
Теорема.Обр.св-во уст-ти выборочной
средней состоит в след:если из генер.сов-ти
сделать неск-ко выборок достат.больш.объёма,
то выборочные средние будут приблизит.равны
м-у собой. Исправленная выборочн.дисперсия:
*M(X)=M(X).
В доказ-ве предполаг,что выборка
повторная. Замечание:из Т.Чебышева
след,что выборочная средняя явл.и
состоятельной оценкой ген.средней.
Теорема.Обр.св-во уст-ти выборочной
средней состоит в след:если из генер.сов-ти
сделать неск-ко выборок достат.больш.объёма,
то выборочные средние будут приблизит.равны
м-у собой. Исправленная выборочн.дисперсия:

42.Интерв-е
оценки парам-в.Построение доверит.интерв.для
генер.средней по выбороч.средней.Объём
повторной и бесповт.выборок.Интерв.оценкой
параметра Ѳ наз-ся интервал (α,β), кот.с
заданной вероятностью γ
накрывает неизв.значение параметра Ѳ.
Такой интерв.(α,β)наз-сядоверит-м интерв.,
а вероятность γ—доверит.вероятностью,или
уровнем надёжности.
 --∆<
Ѳ
<
+∆.
Наибольш.отклонение ∆ выбороч-го
значения парам-ра от его истинного
знач-я наз-ся предельн.ошибкой
выборки.Доверит.интервал ур-ня надёжности
γ для генер.средней ɑ имеет вид:
--∆<
Ѳ
<
+∆.
Наибольш.отклонение ∆ выбороч-го
значения парам-ра от его истинного
знач-я наз-ся предельн.ошибкой
выборки.Доверит.интервал ур-ня надёжности
γ для генер.средней ɑ имеет вид: -∆<ɑ<
+∆,
где ∆--предельная оштбка выборки,
завис.от γ. Объём выборки n
опред-ся ур-ем надёжности γ и
предельн.ошибкой ∆. Объём повтор-й
выборки n=
-∆<ɑ<
+∆,
где ∆--предельная оштбка выборки,
завис.от γ. Объём выборки n
опред-ся ур-ем надёжности γ и
предельн.ошибкой ∆. Объём повтор-й
выборки n=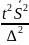 ,
бесповторной— n=
,
бесповторной— n=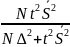 .
.
