17. Непрерывность сложной функции

Если функция   непрерывна в точке  , а функция   непрерывна в точке  , где  , то сложная функция  непрерывна в точке  .

Доказательство. Пусть  . Тогда в силу непрерывности в точке   функции   последовательность    сходится к  . Но тогда, в силу непрерывности уже функции   в точке  , последовательность   сходится к . Итак, из определения Гейне следует, что функция   непрерывна в точке  .

Если считать, что существуют пределы   при   и   при  , то в теореме доказано, что 

Это равенство можно понимать как правило замены переменной при нахождении пределов.

18. Теоремы Вейерштрасса для непрерывных функций на отрезке

Напомним, что функция   непрерывна на отрезке  , если она непрерывна во всех точках интервала   и непрерывна справа в точке   и слева в точке  .

Для таких функций имеет место ряд важных теорем.

Теорема 6.2.1 (первая теорема Вейерштрасса). Если функция   непрерывна на отрезке  , то она ограничена на нем.

Необходимо доказать, что существует  , что для всех   выполняется  .

Доказательство (от противного). Пусть для всякого   найдется такая точка  , что  :

для   найдется  ;

для   найдется   и т. д.,

. . . . . . . .

для   найдется   и т. д.,

. . . . . . . .

Итак, построена последовательность   такая, что для всех  :  . Ясно, что  . Последовательность  , т. е. ограничена. Следовательно, по теореме Больцано - Вейерштрасса, существует подпоследовательность   такая, что . Так как функция   непрерывна на отрезке  , она непрерывна и в точке  . Итак, имеем  , но по построению  , что является противоречием.

Теорема 6.2.2 (вторая теорема Вейерштрасса). Непрерывная функция   на отрезке   достигает в некоторых точках отрезка   своих точных верхней и нижней границ, т. е. существуют   такие, что 

Доказательство. Докажем существование точки максимума функции  , т.е. точки  , в которой значение функции равно точной верхней грани множества значений функции  . По предыдущей теореме 6.2.1 непрерывная на отрезке   функция   является ограниченной на этом отрезке, следовательно, ограничена сверху, например, числом  , т. е. для всех  . Тогда существует точная верхняя граница  множества значений функции   на отрезке    , т.е. такое число  , что

1) для всех  ;

2) для любого   существует точка    .

Возьмем последовательные значения    Тогда построена последовательность  . Эта последовательность ограничена. Следовательно, по теореме Больцано - Вейерштрасса из нее можно выделить подпоследовательность   такую, что  . Функция   непрерывна в точке  .

Следовательно,  , но, с другой стороны, для всех   выполняется  . В силу свойства 3.2.5 сходящихся последовательностей заключаем, что  . Итак,  .

Замечание 6.2.1. Если функция разрывна, то теорема 6.2.2, вообще говоря, неверна. Например,  ,   (см. рис. 6.2.1). Значение, равное  , функцией не достигается.

Рис. 6.2.1 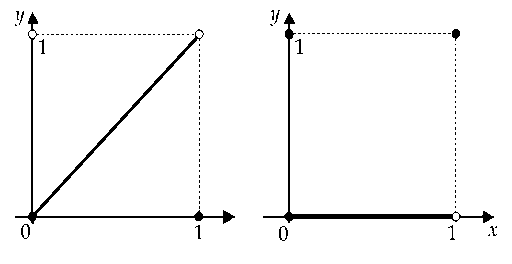                                                  Рис. 6.2.2

Теорема 6.2.3. Если функция   непрерывна на отрезке  , ее значения на концах отрезка   и   не равны нулю и имеют разные знаки, то на интервале   имеется по крайней мере одна точка   такая, что  .

Доказательство (метод Больцано деления отрезка пополам). Пусть   (см. рис. 6.2.3).

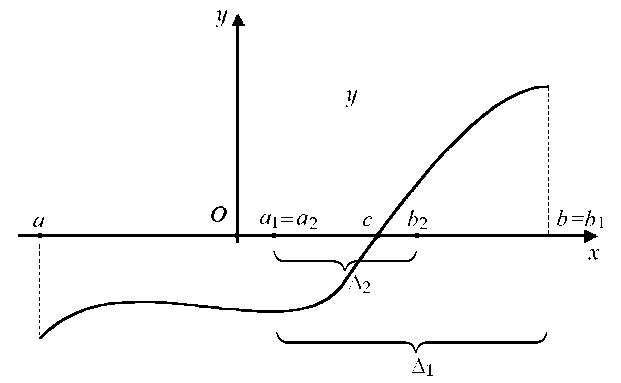Рис. 6.2.3

Обозначим отрезок  . Разделим его пополам. Если в середине отрезка   функция равна нулю, то все доказано. Если нет, то обозначим за   ту из половин отрезка  , на концах которой функция   имеет разные знаки:  . Разделим отрезок   пополам. Если в середине отрезка   функция равна нулю, то все доказано. Если нет, то обозначим за   ту из половин отрезка  , на концах которой функция   имеет разные знаки:  . Рассуждая таким образом, мы либо на каком-то шаге получим точку, в которой функция обращается в нуль, и все доказано, либо построим систему вложенных отрезков, длины которых стремятся к нулю, и для всех   выполняются неравенства  . Следовательно, по теореме Кантора существует точка  , принадлежащая всем отрезкам  . Поэтому   и  . Тогда, с одной стороны, 

с другой стороны, в силу непрерывности функции   в точке  , 

Следовательно,  .

Теорема 6.2.4. Если функция   непрерывна на отрезке  , причем  , и   -- произвольное число такое, что , то на интервале   найдется по крайней мере одна точка  , в которой    т. е. непрерывная на отрезке функция принимает все промежуточные значения между ее значениями на концах отрезка .

Доказательство. Рассмотрим функцию  , где  . Функция   непрерывна на отрезке  , и ,  . Следовательно, по теореме 6.2.3 существует точка  . Отсюда, .

Замечание 6.2.2. Если функция разрывна, то теорема, вообще говоря, неверна. Например, можно взять функцию  . Числовые значения из промежутка   этой функцией не принимаются (см. рис. 6.2.2).

Просто на всякии случай

Определение Функция f (x) называется равномерно непрерывной на множестве D ⊂ R , если для ε>0, найдется δ(ε) > 0 , такое что для любых двух, x₁, x₂ ∈ D , удовлетворяющих условию x x 1 2 − < δ , выполняется неравенство f x f x ( ) ( ) 1 2− < ε

Примером равномерно непрерывной функции является y = x 2