
Магнитное поле в вакууме
В 1820 году Эрстед обнаружил, что магнитная стрелка устанавливается определенным образом по отношению к проводу, по которому идет ток. Это значит, что вокруг проводника с током существует магнитное поле, вызванное движением зарядов. Далее было установлено экспериментально, что магнитное поле действует на движущиеся заряды и не действует на покоящиеся.
Cила Лоренца.
Опыт показывает, что сила, действующая
на заряд q, зависит от
его величины, положения и скорости. Эту
силу разделяют на две составляющие –
электрическую
![]() (не
зависит от скорости заряда) и магнитную
(не
зависит от скорости заряда) и магнитную
![]() (она
зависит от его скорости). Пусть магнитное
поле описывается вектором магнитной
индукции
(она
зависит от его скорости). Пусть магнитное
поле описывается вектором магнитной
индукции
![]() .
Опыт показывает, что на заряд q,
движущийся со скоростью
.
Опыт показывает, что на заряд q,
движущийся со скоростью
![]() ,
действует магнитная сила
,
действует магнитная сила
=![]() , (50)
, (50)
по которой можно определить вектор . На покоящийся заряд в магнитном поле сила не действует. Сила перпендикулярна вектору скорости заряда , поэтому она работы не совершает. Если есть еще и электрическое поле, то результирующая сила (она называется силой Лоренца) равна
![]() . (51)
. (51)
Магнетизм как релятивистский эффект. Изложение этого вопроса выходит за рамки данного курса, однако некоторое представление о релятивистской природе магнетизма можно получить из следующих не строгих соображений.
Рис. 17
Со стороны электрического поля нити на заряд действует сила отталкивания
![]() . (52)
. (52)
Пусть нить движется вправо со скоростью
v (рис.17, б). С точки
зрения покоящегося наблюдателя длина
нити уменьшилась (была
![]() ,
а стала
,
а стала
![]() ),
так как согласно специальной теории
относительности длина движущихся тел
уменьшается в направлении движения:
),
так как согласно специальной теории
относительности длина движущихся тел
уменьшается в направлении движения:
![]() . (53)
. (53)
Поскольку заряд – релятивистский инвариант, величина заряда нити при этом не изменилась:
![]() ,
,
где
![]() - линейная плотность заряда движущейся
нити. Подставляя в последнее равенство
из (53), получим
- линейная плотность заряда движущейся
нити. Подставляя в последнее равенство
из (53), получим
![]() ,
(54)
,
(54)
откуда следует, что линейная плотность заряда увеличилась. Следовательно, должна увеличиться и сила:
![]() ,
(55)
,
(55)
![]() .
(56)
.
(56)
Умножим обе части последнего равенства на 1- 2/c2 :
![]() ,
,
после чего выразим из последнего равенства F:
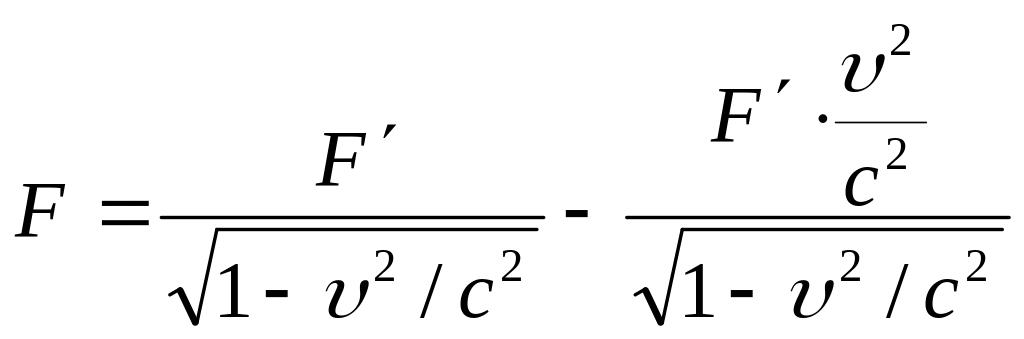 . (57)
. (57)
С точки зрения движущегося вместе с нитью наблюдателя существует только кулоновское отталкивание между зарядом и нитью (первое слагаемое), второе слагаемое равно нулю. А с точки зрения покоящегося наблюдателя сила Кулона увеличилась по модулю, но появилась дополнительная сила притяжения, которая в 2/c2 меньше кулоновской и как раз и представляет собой магнитную силу.
Разделив выражение (57) на q, получим аналогичное соотношение для напряженностей
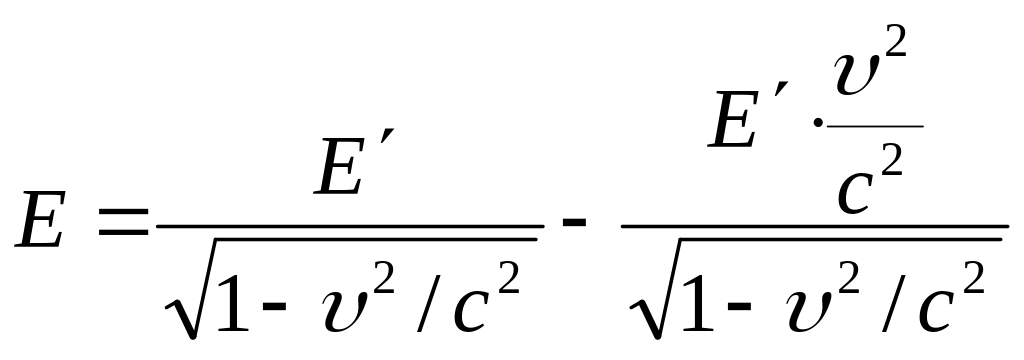 . (58)
. (58)
Из этого следует, что покоящийся наблюдатель воспринимает поле движущейся нити, как изменившееся на величину (второго слагаемого), которая связана со скоростью движения зарядов нити. Таким образом, движущиеся заряды изменяют поле. И поскольку причина этого изменения именно и только заряды движущиеся, данное изменение поля трактуется как появление магнитного поля. Данная трактовка экспериментально подтверждается также и тем, что поле движущихся зарядов действует на магнитную стрелку и вообще по своим проявлениям очень похоже на поле постоянного магнита.
Магнитное поле равномерно движущегося заряда. Опыт показывает, что точечный заряд q, движущийся со скоростью , создает поле с магнитной индукцией
![]() , (59)
, (59)
где магнитная постоянная![]() =410-7
Гн/м;
-
радиус-вектор, проведенный от заряда q
к точке наблюдения. Для магнитных полей,
также как и для электрических, справедлив
принцип суперпозиции.
=410-7
Гн/м;
-
радиус-вектор, проведенный от заряда q
к точке наблюдения. Для магнитных полей,
также как и для электрических, справедлив
принцип суперпозиции.
Закон Био-Саварра. Рассмотрим
магнитное поле, создаваемое постоянными
электрическими токами. Подставим в (59)
вместо q малый заряд![]() (тогда
следует заменить на
(тогда
следует заменить на
![]() ,
из-за малости
):
,
из-за малости
):
![]() .
(60)
.
(60)
Так как
,
![]() и
и
![]() ,
то после подстановки в (60), получим:
,
то после подстановки в (60), получим:
![]() =
=
![]() ,
,
где ↑↑ , что всегда выполняется для тонкого провода. Мы получили закон Био-Саварра
![]() . (61)
. (61)
Учитывая, что
![]() (см. вывод формулы между 60 и 61), вектор
равен
(см. вывод формулы между 60 и 61), вектор
равен
![]() ,
или
,
или
![]() . (62)
. (62)
Теорема Гаусса для вектора . Графически магнитное поле может быть представлено линиями вектора , касательная к которым в каждой точке совпадает с направлением вектора , а густота линий равна его модулю. Магнитное поле не имеет специальных магнитных источников, что и выражает теорема Гаусса для поля вектора : Поток вектора сквозь любую замкнутую поверхность равен нулю:
![]() . (63)
. (63)
Эта теорема выражает тот факт, что линии вектора не имеют ни начала, ни конца. Поэтому число линий, выходящих из любого объема, ограниченного замкнутой поверхностью S , всегда равно числу линий, входящих в этот объем. Отсюда, поток вектора сквозь незамкнутую поверхность S, ограниченную некоторым замкнутым контуром, не зависит от формы этой поверхности.
Теорема о циркуляции вектора (для магнитного поля постоянных токов в вакууме). Циркуляция вектора поля по произвольному замкнутому контуру Г равна произведению о на алгебраическую сумму токов, охватываемых контуром Г:
![]() =
оI
, (64)
=
оI
, (64)
г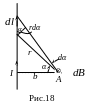 де
де
![]() .
Каждый ток в сумме – величина
алгебраическая: ток считается >0, если
направление движения положительных
зарядов в нем связано с направлением
обхода контура правилом правого винта.
.
Каждый ток в сумме – величина
алгебраическая: ток считается >0, если
направление движения положительных
зарядов в нем связано с направлением
обхода контура правилом правого винта.
Так как правая часть выражения (64) не равна нулю, данное поле не потенциально. Подобные поля называют вихревыми, или соленоидальными. Теорема о циркуляции может быть применена для расчета поля вектора . Сравним расчет магнитного поля прямого тока при помощи закона Био-Саварра с расчетом, в котором используется теорема о циркуляции вектора .
Магнитное поле прямого тока. Рассмотрим бесконечный тонкий прямой проводник, по которому течет ток I (рис.18). В соответствии с (61) в произвольной точке А векторы от всех элементов тока имеют одинаковое направление – за плоскость рисунка. Поэтому сложение векторов можно заменить сложением их модулей (удобнее в качестве угла α взять не угол между dl и r, а дополнительный к нему, поэтому вместо синуса - косинус)
![]() .
.
Из рисунка 18 видно, что
![]() и
и
![]() ,
,
![]() .
.
Проинтегрируем это выражение в пределах изменения от -/2 до +/2,
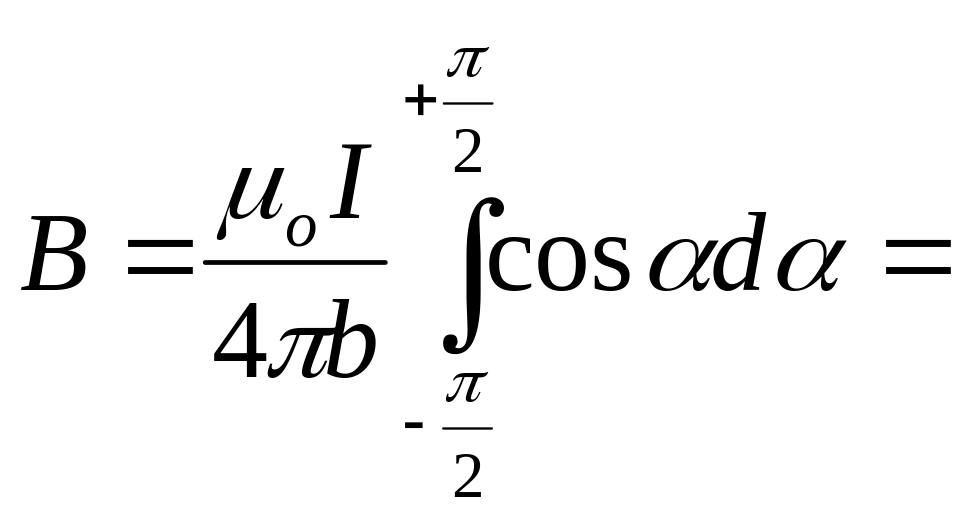
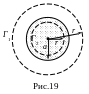
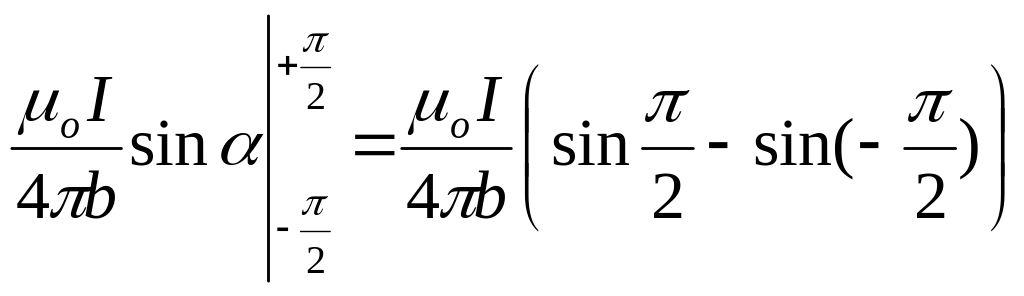 =
=![]() ,
,
![]() . (65)
. (65)
Решим эту же задачу при помощи теоремы
о циркуляции. Причем в данном случае
откажемся от предположения о тонком
проводнике. Пусть постоянный ток I
течет вдоль бесконечного прямого
провода, имеющего круглое сечение
радиуса а, перпендикулярно рисунку
19. Найдем индукцию поля
снаружи
и внутри провода. Из симметрии задачи
следует, что силовые линии должны иметь
вид перпендикулярных проводу окружностей
с центром на оси провода. Причем модуль
вектора
должен
быть одинаков для всех точек, расположенных
на одинаковом расстоянии r
от оси. Для контура Г1 по теореме
о циркуляции
![]() ,
,
![]() при (
при (![]() ),
что по смыслу совпадает с (65) ; для контура
Г2:
),
что по смыслу совпадает с (65) ; для контура
Г2:
![]() ,
так как внутрь этого контура попадает
только часть тока, пропорциональная
отношению сечений.
,
так как внутрь этого контура попадает
только часть тока, пропорциональная
отношению сечений.
![]() при (
при (![]() ).
).
Закон Ампера. Каждый носитель тока испытывает действие магнитной силы. Действие этой силы передается проводнику, по которому движутся заряды. В результате магнитное поле действует с определенной силой на сам проводник с током. Величину этой силы и определяет закон Ампера.
Пусть объемная плотность носителей
тока в проводнике равна .
В элементе объема dV
проводника содержится заряд ρdV,
который можно считать точечным вследствие
его малости. Тогда элементарная магнитная
сила Лоренца, действующая на этот заряд,
равна
![]() ,
где
,
где
![]() -
скорость упорядоченного движения
зарядов. Плотность тока
-
скорость упорядоченного движения
зарядов. Плотность тока
![]() ,
поэтому
,
поэтому
![]() .
Если ток течет по тонкому проводу, то
,
.
Если ток течет по тонкому проводу, то
,
![]() . (66)
. (66)
Это и есть закон Ампера, выражающий силу, действующую на элемент тонкого провода , по которому течет ток I.
Теперь можно дать определение основной электрической единицы в системе СИ, ампера [А]. Пусть по двум параллельным бесконечно длинным и тонким проводникам течет одинаковый ток I.
По закону Ампера на единицу длины каждого проводника будет действовать сила F=IB1=IB2, где магнитные индукции B1=B2 определяются формулой (65):
![]() .
.
Таким образом, сила, действующая на единицу длины любого из проводов, однозначно связана с величиной тока. Силу легко измерить, например, с помощью весов. Отсюда следует определение основной электрической единицы в СИ – единицы силы тока. Ампер [A] – это сила постоянного тока, который, проходя по двум параллельным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенных на расстоянии 1 м друг от друга в вакууме, вызывает между ними силу взаимодействия, равную 2∙10-7 Н на каждый метр длины. Единица заряда кулон [Кл] не является основной и определяется через ампер: кулон есть заряд, проходящий за 1 с через поперечное сечение однородного изотропного проводника, по которому течет ток 1 А.

 Магнитное
поле соленоида. Соленоид это провод,
намотанный на цилиндрическую поверхность
(на рис.20 соленоид изображен в сечении
плоскостью, проходящей через его ось).
Пусть по этому проводу течет ток I
и на единицу длины соленоида приходится
n витков. Если шаг
витка мал, то каждый виток можно
приблизительно считать окружностью.
Опыт и расчет показывают, что чем длиннее
соленоид, тем меньше поле снаружи, а при
достаточно длинном соленоиде поле
снаружи практически отсутствует. Поле
внутри из соображений симметрии должно
быть направлено вдоль оси соленоида и
составлять с направлением тока в витках
правовинтовую систему. Эти же соображения
подсказывают форму контура – прямоугольник,
расположенный, как показано на рисунке.
Вклад от вертикальных участков контура
равен нулю, так как векторы
и
перпендикулярны
друг другу. Вклад от внешнего участка
контура равен нулю, так как снаружи
=0.
Поэтому циркуляция по данному контуру
определяется только его внутренним
участком и равна
Магнитное
поле соленоида. Соленоид это провод,
намотанный на цилиндрическую поверхность
(на рис.20 соленоид изображен в сечении
плоскостью, проходящей через его ось).
Пусть по этому проводу течет ток I
и на единицу длины соленоида приходится
n витков. Если шаг
витка мал, то каждый виток можно
приблизительно считать окружностью.
Опыт и расчет показывают, что чем длиннее
соленоид, тем меньше поле снаружи, а при
достаточно длинном соленоиде поле
снаружи практически отсутствует. Поле
внутри из соображений симметрии должно
быть направлено вдоль оси соленоида и
составлять с направлением тока в витках
правовинтовую систему. Эти же соображения
подсказывают форму контура – прямоугольник,
расположенный, как показано на рисунке.
Вклад от вертикальных участков контура
равен нулю, так как векторы
и
перпендикулярны
друг другу. Вклад от внешнего участка
контура равен нулю, так как снаружи
=0.
Поэтому циркуляция по данному контуру
определяется только его внутренним
участком и равна![]() .
Так как контур охватывает ток
.
Так как контур охватывает ток
![]() ,
по теореме о
циркуляции
,
по теореме о
циркуляции
![]() .
Следовательно, индукция магнитного
поля внутри соленоида равна
.
Следовательно, индукция магнитного
поля внутри соленоида равна
![]() . (67)
. (67)
Сила, действующая на контур с током. Результирующая сил Ампера, действующих на замкнутый контур с током в магнитном поле, определяется интегрированием выражения (66):
![]() . (68)
. (68)
Если магнитное поле однородно, то вектор
можно
вынести из-под интеграла и задача
сводится к вычислению интеграла
![]() .
Этот интеграл представляет собой
замкнутую цепочку векторов
и поэтому он равен нулю, значит и
.
Этот интеграл представляет собой
замкнутую цепочку векторов
и поэтому он равен нулю, значит и
![]() =0.
Т.е. в однородном магнитном поле на
замкнутый контур как целое сила не
действует.
=0.
Т.е. в однородном магнитном поле на
замкнутый контур как целое сила не
действует.
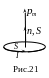 Магнитный
момент контура с током. Рассмотрим
плоский контур из тонкого провода
достаточно малых размеров, по которому
течет ток I. Такой
контур называется элементарным.
Магнитным моментом элементарного
контура называется произведение
Магнитный
момент контура с током. Рассмотрим
плоский контур из тонкого провода
достаточно малых размеров, по которому
течет ток I. Такой
контур называется элементарным.
Магнитным моментом элементарного
контура называется произведение
![]() , (69)
, (69)
где
![]() -
ток,
-
ток,
![]() -
вектор, равный площади контура по
величине и совпадающий по направлению
с положительной нормалью к контуру
(рис.21).
-
вектор, равный площади контура по
величине и совпадающий по направлению
с положительной нормалью к контуру
(рис.21).
 Контур
с током в однородном магнитном поле.
Если замкнутый контур, по которому течет
ток, поместить в однородное магнитное
поле, то результирующий момент
амперовых сил
Контур
с током в однородном магнитном поле.
Если замкнутый контур, по которому течет
ток, поместить в однородное магнитное
поле, то результирующий момент
амперовых сил
![]() в общем случае не равен нулю. Действительно,
поместим прямоугольную рамку из тонкого
провода, по которому течет ток I,
в однородное магнитное поле с индукцией
(рис.22).
На рис. 22(а) стороны b
расположены перпенди-кулярно вектору
,
а стороны а – под произвольным
углом. На каждую сторону рамки будет
действовать своя сила Ампера:
в общем случае не равен нулю. Действительно,
поместим прямоугольную рамку из тонкого
провода, по которому течет ток I,
в однородное магнитное поле с индукцией
(рис.22).
На рис. 22(а) стороны b
расположены перпенди-кулярно вектору
,
а стороны а – под произвольным
углом. На каждую сторону рамки будет
действовать своя сила Ампера:
![]() -
на стороны а;
-
на стороны а;
![]() - на стороны b, где
векторы
- на стороны b, где
векторы
![]() и
и
![]() имеют
направление тока на своем участке.
Поскольку две силы
имеют
направление тока на своем участке.
Поскольку две силы
![]() лежат в плоскости рамки, равны по модулю
и направлены в противоположные стороны,
они будут только растягивать (или
сжимать) рамку. Пара сил
лежат в плоскости рамки, равны по модулю
и направлены в противоположные стороны,
они будут только растягивать (или
сжимать) рамку. Пара сил
![]() не лежит в плоскости рамки, и поэтому
создает вращательный момент. Его удобно
вычислить, если изобразить рамку
по-другому: так, чтобы стороны b
были перпендикулярны плоскости листа
(рис.22 б). Пара сил
создает момент величиной
не лежит в плоскости рамки, и поэтому
создает вращательный момент. Его удобно
вычислить, если изобразить рамку
по-другому: так, чтобы стороны b
были перпендикулярны плоскости листа
(рис.22 б). Пара сил
создает момент величиной
![]() ,
что с учетом (69) можно записать в виде
векторного произведения
,
что с учетом (69) можно записать в виде
векторного произведения
![]() , (70)
, (70)
где вектор
![]() перпендикулярен как вектору магнитного
момента контура
перпендикулярен как вектору магнитного
момента контура![]() ,
так и вектору
;
,
так и вектору
;![]() -
угол между векторами
(или
)
и
.
Если вектор
перпендикулярен вектору
(плоскость
рамки параллельна вектору
),
то момент
максимален, и рамка будет поворачиваться
по полю до тех пор, пока эти векторы не
станут параллельными. Когда
↑↑
,
момент сил
=0
и положение контура будет устойчивым.
Если
↑↓
,
момент сил тоже равен нулю, но положение
контура будет неустойчивым.
-
угол между векторами
(или
)
и
.
Если вектор
перпендикулярен вектору
(плоскость
рамки параллельна вектору
),
то момент
максимален, и рамка будет поворачиваться
по полю до тех пор, пока эти векторы не
станут параллельными. Когда
↑↑
,
момент сил
=0
и положение контура будет устойчивым.
Если
↑↓
,
момент сил тоже равен нулю, но положение
контура будет неустойчивым.
Покажем, что выбор именно прямоугольного контура, да еще и определенным образом расположенного по отношению к магнитному полю, не нарушает общности полученного выше результата. Действительно, элемент контура произвольной формы можно разложить на две составляющие: параллельную и перпендикулярную вектору . На первую из них сила ампера действовать не будет (sin =0), а вторая будет вести себя как сторона b прямоугольного контура с током. Поэтому в однородном магнитном поле любой плоский контур с током будет поворачиваться, стремясь установиться своим магнитным моментом параллельно полю.
В неоднородном магнитном поле сила, действующая на контур, уже не будет равна нулю. В частности, сила, действующая на элементарный контур с током, равна (без вывода)
![]() .
.
Поэтому элементарный контур с током в неоднородном магнитном поле будет не только поворачиваться к положению устойчивого равновесия (при котором ↑↑ ), но и втягиваться в область поля с большей магнитной индукцией .
Работа при перемещении контура с током. Покажем, что при перемещении элементарного контура с током в магнитном поле силы Ампера совершают работу
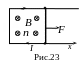
![]() , (71)
, (71)
где
![]() -
приращение магнитного потока сквозь
контур. Рассмотрим сначала частный
случай: контур с подвижной перемычкой
длины l находится в
однородном магнитном поле, перпендикулярном
плоскости рисунка 23. Согласно (66) на
перемычку действует сила Ампера
-
приращение магнитного потока сквозь
контур. Рассмотрим сначала частный
случай: контур с подвижной перемычкой
длины l находится в
однородном магнитном поле, перпендикулярном
плоскости рисунка 23. Согласно (66) на
перемычку действует сила Ампера
![]() .
При перемещении вправо на
.
При перемещении вправо на
![]() эта сила совершает положительную работу
эта сила совершает положительную работу
![]() , (72)
, (72)
где dS – приращение
площади, ограниченной контуром. Магнитный
поток считается Ф>0, если нормаль
к площади контура образует с направлением
тока в нем правовинтовую систему, как
на рис.23. Полученное выражение справедливо
при любом направлении вектора
.
Действительно, разложим этот вектор на
три составляющие:
![]() .
Составляющая
.
Составляющая
![]() параллельна току, поэтому соответствующая
сила Ампера равна нулю; составляющая
параллельна току, поэтому соответствующая
сила Ампера равна нулю; составляющая
![]() дает силу, перпендикулярную перемещению,
поэтому работы она не совершает. Остается
только
дает силу, перпендикулярную перемещению,
поэтому работы она не совершает. Остается
только
![]() ,
ее и следует подставить в (72) в случае
произвольного направления вектора
.
Но
,
ее и следует подставить в (72) в случае
произвольного направления вектора
.
Но
![]() в любом случае, и мы опять приходим к
формуле (71). Перейдем теперь к рассмотрению
любого контура при произвольном его
перемещении в стационарном неоднородном
магнитном поле. Разобьем мысленно этот
контур на бесконечно малые элементы
тока и рассмотрим их бесконечно малые
перемещения, в пределах которых поле
можно считать однородным. Сложив
элементарные работы для всех элементов,
мы вновь придем к (71). Чтобы получить
полную работу при перемещении из
положения 1 в положение 2 достаточно
проинтегрировать:
в любом случае, и мы опять приходим к
формуле (71). Перейдем теперь к рассмотрению
любого контура при произвольном его
перемещении в стационарном неоднородном
магнитном поле. Разобьем мысленно этот
контур на бесконечно малые элементы
тока и рассмотрим их бесконечно малые
перемещения, в пределах которых поле
можно считать однородным. Сложив
элементарные работы для всех элементов,
мы вновь придем к (71). Чтобы получить
полную работу при перемещении из
положения 1 в положение 2 достаточно
проинтегрировать:
![]() . (73)
. (73)
При постоянном токе
![]() ,
где
,
где
![]() и
и
![]() - магнитные потоки сквозь контур в
конечном и начальном положениях контура.
- магнитные потоки сквозь контур в
конечном и начальном положениях контура.
