
- •2.Вычисление двойного нтеграла в декартовых координатах.
- •5. Вычисление объёмов тел площадей плоских фигур с помощью двойного интеграла.
- •7. Механические приложения двойного интеграла.
- •8. Определение и свойства тройного интеграла.
- •4)Если в области r,то ;
- •5)Если в области r и , то ;
- •6)Если на r и области r и s являются непересекающимися , то . Здесь означает объединение этих двух областей.
- •10.Вычисление тройного интеграла в цилиндрических координатах
- •11. Тройной интеграл в сферических координатах.
- •12.Механические приложения тройного интеграла.
- •13. Криволинейный интеграл I рода. Основные свойства кри-I.
- •14.Криволинейный интеграл II рода. Основные свойства кри-II.
- •15. Формула Остроградского – Грина.
- •16.Приложения кри(1-2)
- •17.Поверхностный интеграл 1-го рода
- •18.Поверхностный интеграл II рода.
- •19.Формула Стокса
- •20. Пови-2 по замкнутым поверхностям. Формула Астроградского.
- •21.Понятие скалярного поля. Поверхности и линии уровня.
- •22.Производная скалярного поля по направлению. Градиент.
- •23. Понятие векторного поля. Векторные линии векторного поля.
- •24.Циркуляция и ротор векторного поля.
- •25.Поток и дивергенция векторного поля.
- •26.Оператор Гамильтона и некоторые его применения.
- •27.Потенциальное,соленоидальное и гармоническое векторные поля.
- •28.Понятие числового ряда и его суммы. Свойства числовых рядов.
- •29.Необходимый признак сходимости ряда.
- •30.Интегральный признак Коши.
- •31.Признак сравнения рядов с положительными членами.
- •32.Признак Даламбера.
- •33.Радикальный признак Коши
- •34.Знакопеременные ряды. Абсолютная и условная сходимость рядов.
- •35.Знакочередующиеся ряды. Признак Лейбница.
- •36.Функциональные ряды. Свойства правильно сходящихся рядов.
- •37.Степенные ряды. Область сходимости.
- •38.Свойства степенных рядов.
- •39.Ряды Тейлора и Маклорена.
38.Свойства степенных рядов.
Сформулируем без доказательства основные свойства степенных рядов.
1)Сумма
![]() степенного ряда (7.3) является непрерывной
функцией в интервале сходимости
.
степенного ряда (7.3) является непрерывной
функцией в интервале сходимости
.
2)Степенные ряды
![]() и
и
![]() ,
имеющие радиусы сходимости соответственно
,
имеющие радиусы сходимости соответственно
![]() и
и
![]() ,
можно почленно складывать, вычитать и
умножать. Радиус сходимости произведения,
суммы и разности рядов не меньше, чем
меньшее из числе
и
.
,
можно почленно складывать, вычитать и
умножать. Радиус сходимости произведения,
суммы и разности рядов не меньше, чем
меньшее из числе
и
.
3)Степенной ряд внутри интервала сходимости можно почленно дифференцировать. Для ряда
![]()
при
![]()
![]() . (7.6)
. (7.6)
4)Степенной ряд можно почленно интегрировать на каждом отрезке, расположенном внутри интервала сходимости. Для ряда (7.3) при выполняется равенство
![]() Ряды
(7.6) и (7.7) имеют тот же радиус сходимости,
что и исходный степенной ряд. Перечисленные
свойства остаются справедливыми и для
степенных рядов вида .
Ряды
(7.6) и (7.7) имеют тот же радиус сходимости,
что и исходный степенной ряд. Перечисленные
свойства остаются справедливыми и для
степенных рядов вида .
39.Ряды Тейлора и Маклорена.
Для приложений
важно уметь данную функцию
представлять в виде суммы степенного
ряда.Для любой функции
,
определенной в окрестности точки
и имеющей в ней производные до
![]() -го
порядка включительно, справедлива
формула Тейлора:
-го
порядка включительно, справедлива
формула Тейлора:
![]() ,
,
где
![]() ,
остаточный член в форме Лагранжа. Причем
число
,
остаточный член в форме Лагранжа. Причем
число
![]() можно записать в виде
можно записать в виде
![]() ,
где
,
где
![]() .
.
Формулу (7.8) можно записать в виде
![]() ,
,
где
![]()
многочлен Тейлора.
многочлен Тейлора.
Если функция
имеет производные любых порядков (т.е.
бесконечно дифференцируема) в окрестности
точки
и остаточный член
![]() стремится к нулю при
(
стремится к нулю при
(![]() ),
то из формулы Тейлора получается
разложение функции
по степени
),
то из формулы Тейлора получается
разложение функции
по степени
![]() ,
называемое рядом
Тейлора:
,
называемое рядом
Тейлора:
![]() Если
в ряде Тейлора положить
,
то получим разложение функции по степеням
в так называемый ряд
Маклорена:
Если
в ряде Тейлора положить
,
то получим разложение функции по степеням
в так называемый ряд
Маклорена:
![]()
Отметим, что ряд Тейлора можно формально построить для любой бесконечно дифференцируемой функции (это необходимое условие) в окрестности точки . Но отсюда еще не следует, что он будет сходиться к данной функции ;он может оказаться расходящимся или сходится, но не к функции .
В следующей теореме (которую примем без доказательства) сформулировано необходимое и достаточное условие сходимости ряда Тейлора к функции .
Теорема Для того чтобы ряд Тейлора (7.9) функции сходился к функции в точке , необходимо и достаточно, чтобы в этой точке остаточный член формулы Тейлора (7.8) стремился к нулю при , т.е. чтобы .
Для разложения функции в ряд Маклорена (7.10) нужно:
найти производные
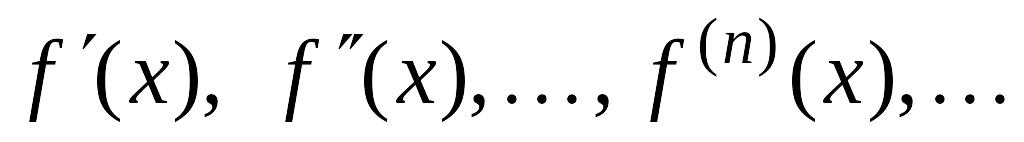 ;
;вычислить значения производных в точке ;
выписать ряд (7.10) для заданной функции и найти его интервал сходимости;
найти интервал
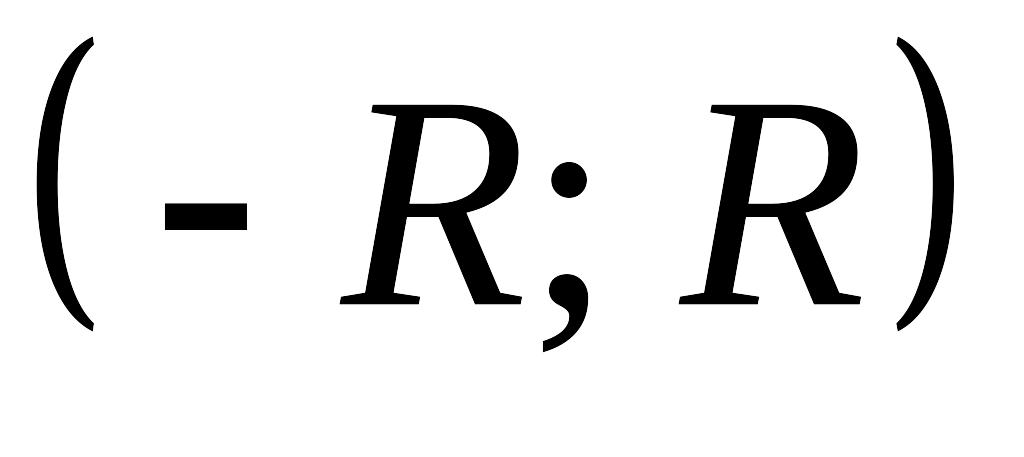 ,
в котором остаточный член ряда Маклорена
,
в котором остаточный член ряда Маклорена
 при
.
Если такой интервал существует, то в
нем функция
и сумма ряда Маклорена совпадают.
при
.
Если такой интервал существует, то в
нем функция
и сумма ряда Маклорена совпадают.
