3. Свойства неопределенного интеграла.
Из определений первообразной F(x) неопределенного интеграла от данной функции f(x) на некотором промежутке следуют свойства неопределенного интеграла:
1.
.
2.
.
3.
,
где С – произвольная постоянная.
4.
,
где k
= const.
5.
Замечание. Все вышеперечисленные свойства верны при условии. Что интегралы, фигурирующие в них, рассматриваются на одном и том же промежутке и существуют.
4. Таблица основных неопределенных интегралов.
Действие интегрирования является обратным действию дифференцирования, то есть по заданной производной f(x) надо восстановить начальную функцию F(x). Тогда из определения 2 и таблицы производных получается таблица основных интегралов.
1.
.
2.
.
3.
.
4.
.
5.
.
6.
.
7.
.
8.
.
9.
.
10.
.
11.
.
12.
.
13.
.
14.
.
15.
.
16.
.
В формулах 1-16 С – произвольная постоянная.
Замечание. Интеграл не от любой элементарной функции является элементарной функцией. Параметрами могут служить следующие интегралы, часто встречающиеся в задачах:
- интеграл Пуассона,
- интеграл Френеля,
- интегральный
логарифм,
- интегральный
косинус и синус.
Указанные функции существуют, имеют важное прикладное значение. Для них составлены таблицы значений.
§ 8 Методы интегрирования
1. Непосредственное интегрирование
а) работа с таблицей: предложенный интеграл оказался одним из табличных интегралов. В этом случае требуется безошибочно найти соответствующую формулу таблицы и ею воспользоваться.
Пример 1.
1.
(формула № 14)
2.
(формула № 16)
б) Метод разложения: предложенный интеграл после применения линейных свойств (№№ 4 и 5) неопределенного интеграла заменяется на алгебраическую сумму табличных интегралов.
Пример 2.
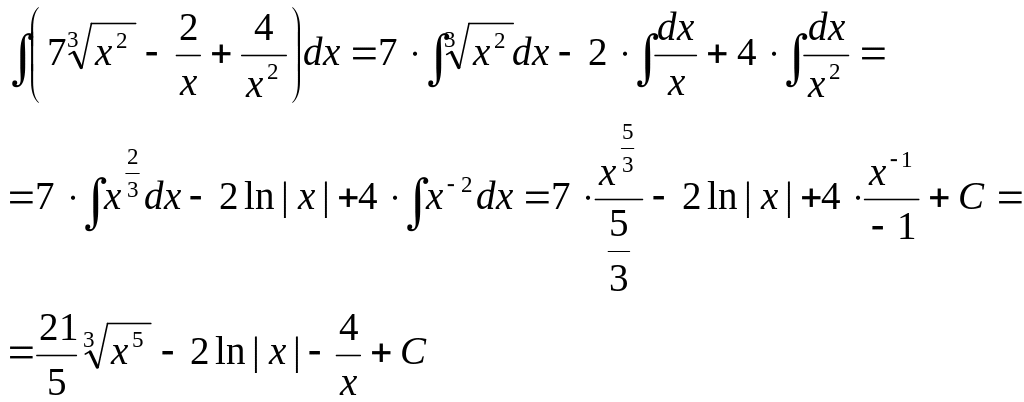
Ответ:
Пример 3.
Ответ:
Пример 4.
Ответ:
в) Подведение под знак дифференциала: предложенный интеграл удается свести к табличному с помощью изменения переменой интегрирования или за счет преобразований под знаком дифференциала. При этом используют следующие формулы:
d(j(x)) = j’(x)dx;
.
Также используют тот факт, что если известен результат
,
то равенство:
Будет справедливо
для любой дифференцируемой функции
.
Пример 5.
Ответ:
.
Пример 6.
.
Ответ:
.
Пример 7.
.
Ответ:
.
Пример 8.
.
Ответ: .
Пример 9.
.
Ответ:
.
2. Интегрирование подстановкой.
Подстановка (или замена переменной) базируется на следующей теореме.
Теорема 1. Если не удается найти интеграл непосредственно, то можно выбрать такую функцию x = j(t), удовлетворяющую условиям:
1) j(t) непрерывна при t (;), соответствующем интервалу xÎ (a;b),
2) дифференцируемая при tÎ (a;b);
3) имеет обратную функцию t = j-1(x), чтобы
|
Был табличный или проще. Иногда для упрощения интеграла можно сделать замену t = (x).
Замечание. Выбор правильной подстановки в значительной степени зависит от искусства вычислителя.
Пример 10.
.
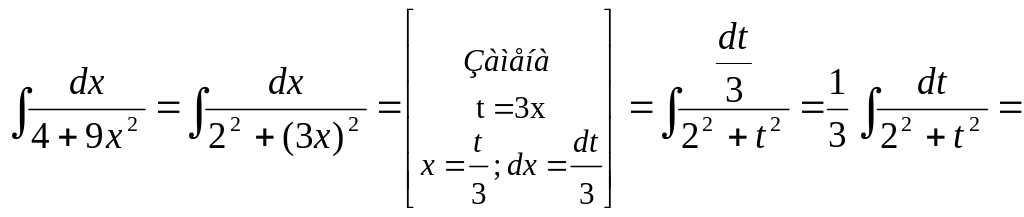
Ответ:
.
П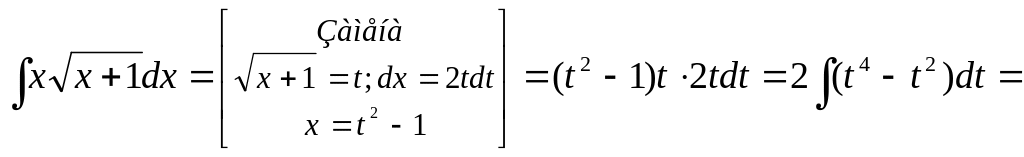
ример
11.
.
Ответ:
.
Пример 12.
.
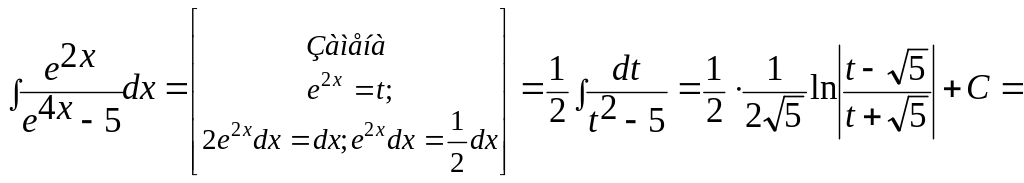
Ответ:
.
Пример 13.
.
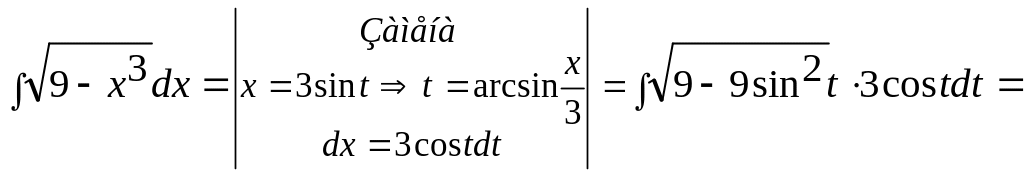
Ответ:
.