
- •1. Рациональные уравнения и методы их решения
- •Методы их решения
- •1. Использование области определения уравнения.
- •2. Разложение на множители.
- •3. Замена переменной.
- •Функциональные методы
- •4. Использование ограниченности функций.
- •5. Использование монотонности функций.
- •2. Рациональные неравенства и методы их решения
- •Алгебраические неравенства.
- •3. Модуль числа. Решение уравнений, содержащих переменную под знаком модуля
- •Основные свойства модуля:
- •I тип уравнений
- •II тип уравнений
- •III тип уравнений
- •IV тип уравнений
- •V тип уравнений
- •VI тип уравнений
- •4. Модуль числа. Решение неравенств, содержащих переменную под знаком модуля
- •1 Способ. Использование геометрического смысла модуля.
- •2 Способ. Использование свойства модулей: модули противоположных чисел равны.
- •3 Способ: Использование определение модуля числа.
- •4 Способ: Решение неравенства на интервалах
- •5.Уравнения. Равносильные уравнения. Уравнения–следствия. Теоремы о равносильных преобразованиях уравнений
- •Преобразования, приводящие к равносильному уравнению
- •Теоремы о равносильных преобразованиях уравнений
- •6. Неравенства. Равносильные неравенства. Неравенства-следствия. Теоремы о равносильных преобразованиях неравенств
- •7. Системы и совокупности уравнений. Основные методы решения систем уравнений
- •Системы и совокупности уравнений
- •8. Системы и совокупности неравенств
- •Основные методы решения систем двух неравенств с двумя неизвестными
- •9. Иррациональные уравнения. Основные методы решения иррациональных уравнений
- •10. Иррациональные неравенства. Основные методы решения иррациональных неравенств
- •11. Показательные уравнения. Основные методы решения показательных уравнений
- •12. Показательные неравенства. Основные методы решения показательных неравенств.
- •13. Логарифмические уравнения. Основные методы решения логарифмических уравнений
- •14 . Логарифмические неравенства. Основные методы решения логарифмических неравенств
- •15. Основные методы решения тригонометрических уравнений
- •16. Основные методы решения тригонометрических неравенств
- •17 . Уравнение с параметрами. Решение линейных уравнений с параметрами.
- •18. Уравнения с параметрами. Решение квадратных уравнений с параметрами
- •19. Методы решения уравнения . Методы решения неравенства
- •20. Обобщающий метод интервалов для решения неравенств
- •21. Основные тригонометрические функции, их свойства, графики
- •22. Обратные тригонометрические функции, графики, свойства
- •1. Метрические соотношения в окружности. Свойства хорд. Свойства секущих и касательных к окружности. Измерение углов, связанных с окружностью
- •Свойства хорд
- •2. Окружность, вписанная в треугольник. Формулы, связывающие элементы треугольника с радиусом вписанной окружности
- •3. Окружность, описанная около треугольника. Формулы, связывающие элементы треугольника с радиусом описанной окружности
- •4. Прямая Эйлера
- •5. Окружность Эйлера
- •6. Вневписанная окружность.
- •7. Центроид треугольника
- •8. Ортоцентр треугольника. Ортотреугольник. Свойства ортоцентра треугольника
- •9. Вписанные четырехугольники. Вписанные многоугольники
- •10. Описанные четырехугольники. Описанные многоугольники
- •11. Теорема Пифагора. Обобщенная теорема Пифагора.
- •12. Теорема Пифагора для четырехугольников.
- •13. Теорема Птолемея.
- •14. Методы геометрических преобразований. Симметрия. Поворот. Параллельный перенос. Подобие. Гомотетия.
- •15. Метод площадей.
- •1.Свойства параллельного проектирования. Изображение плоских фигур. Требования к проекционным чертежам.
- •2. Свойства параллельного проектирования. Изображение многоугольников и тел вращения. Теорема Польке-Шварца.
- •3.Методы построения сечений многогранников.
- •4.Взаимное расположение прямых в пространстве. Скрещивающиеся прямые. Признак скрещивающихся прямых. Угол между скрещивающимися прямыми. Расстояние между скрещивающимися прямыми.
- •Взаимное расположение прямой и плоскости в пространстве. Угол между прямой и плоскостью.
- •Взаимное расположение плоскостей в пространстве. Угол между плоскостями. Двугранный угол. Измерение двугранных углов.
- •Взаимное расположение плоскостей в пространстве. Многогранный угол. Трехгранный угол. Их свойства.
6. Вневписанная окружность.
Опр1. Окружность, касающаяся одной стороны треугольника и продолжений двух других его сторон, называется вневписанной окружностью.
На рис. окружность касается стороны ВС(а) треугольника АВС и продолжений его сторон АС(b) и АВ(с). Центр окружности часто обозначают Iа (окружность касается стороны а), а радиус — rа .
T1.
Центр вневписанной окружности треугольника
лежит на пересечении биссектрис двух
внешних углов и внутреннего угла
треугольника, лежащего против стороны
касания с окружностью. Дано: ∆АВС,
Доказать: существует Iа
— точка пересечения биссектрис углов
CAB,
МСВ, NBC,
где М
 АС,
МС + СА = AM
, N
АС,
МС + СА = AM
, N
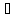 АВ и
NB
+ ВА = NA
. Доказательство:
1) Проведем биссектрису
угла CAB.
Тогда любая ее точка равноудалена от
сторон АС
и АВ
угла. 2) Проведем биссектрису угла МСВ.
Точка Iа
пересечения этой биссектрисы и
биссектрисы угла
CAB
равноудалена от стороны
ВС и продолжений
сторон АВ и АС.
Значит, точка Iа
лежит на биссектрисе угла
CBN.
3)
Таким образом,
Iа
— точка пересечения биссектрисы
внутреннего угла
CAB
и двух биссектрис внешних углов
МСВ и
NBC
треугольника AВС.
АВ и
NB
+ ВА = NA
. Доказательство:
1) Проведем биссектрису
угла CAB.
Тогда любая ее точка равноудалена от
сторон АС
и АВ
угла. 2) Проведем биссектрису угла МСВ.
Точка Iа
пересечения этой биссектрисы и
биссектрисы угла
CAB
равноудалена от стороны
ВС и продолжений
сторон АВ и АС.
Значит, точка Iа
лежит на биссектрисе угла
CBN.
3)
Таким образом,
Iа
— точка пересечения биссектрисы
внутреннего угла
CAB
и двух биссектрис внешних углов
МСВ и
NBC
треугольника AВС.
Если
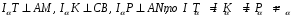 .
.
T2.
Точка касания вневписанной окружности
треугольника делит его периметр пополам.
Дано: ∆ABC,
Iа
— центр вневписанной окружности,
IаК
— радиус вневписанной окружности,
проведенный в точку касания со стороной
ВС.
Доказать: АС + СК = АВ + ВК.
Доказательство.
AT
= АР, СТ = СК , ВК = BP
как отрезки касательных, проведенные
из одной точки. 2АТ
= АТ + АР = AC
+ СТ + АВ + BP
=
=AC
+ CK
+ AB
+ BK
= 2P,где
P
— полупериметр
∆
ABC
. Значит,
AT
=
P,
но
AT
= AC
+ CT
=
= AC
+ CK
= P.
Таким
образом,
AC
+
CK
=
P
=
= AB
+
BK,
т.е. точка
К
касания вневписанной окружности
треугольника делит его периметр пополам.
Для любого треугольника можно построить
три вневписанные окружности.
Т3.
Площадь S
треугольника
АВС
равна
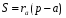 .
Док-во:
.
Док-во:
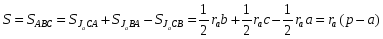

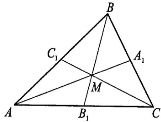
7. Центроид треугольника
Существование центроида (центра тяжести) треугольника и его основное свойство основано на следующей теореме.
Т1.
Три медианы треугольника пересекаются
в одной точке М, которая делит каждую
из них в отношении 2:1, считая от вершин
треугольника. Дано: ∆ABC,
СС1,
АА1,
ВВ1
— медианы
∆ ABC.
Доказать:
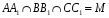 и
и
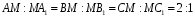 .
Д-во: Пусть М — точка
пересечения медиан СС1,
АА1 треугольника
ABC.
Отметим A2
— середину отрезка AM
и С2
— середину отрезка СМ. Тогда A2C2
— средняя линия треугольника
АМС. Значит,
А2
С2
|| АС
.
Д-во: Пусть М — точка
пересечения медиан СС1,
АА1 треугольника
ABC.
Отметим A2
— середину отрезка AM
и С2
— середину отрезка СМ. Тогда A2C2
— средняя линия треугольника
АМС. Значит,
А2
С2
|| АС
и A2C2 = 0,5*АС. С1А1 — средняя линия треугольника ABC. Значит, А1С1 || АС и А1С1 = 0,5*АС.
Четырехугольник А2С1А1С2 — параллелограмм, так как его противоположные стороны А1С1 и А2С2 равны и параллельны. Следовательно, А2М = МА1 и С2М = МC1. Это означает, что точки А2 и M делят медиану АА2 на три равные части, т. е. AM = 2МА2 . Аналогично СМ = 2MC1. Итак, точка М пересечения двух медиан АА2 и CC2 треугольника ABC делит каждую из них в отношении 2:1, считая от вершин треугольника. Совершенно аналогично доказывается, что точка пересечения медиан АА1 и BB1 делит каждую из них в отношении 2:1, считая от вершин треугольника.
 На
медиане АА1
такой точкой является точка М,
следовательно, точка
М и есть точка
пересечения медиан АА1
и BB1.
На
медиане АА1
такой точкой является точка М,
следовательно, точка
М и есть точка
пересечения медиан АА1
и BB1.
Таким
образом,

T2.
Докажите, что отрезки, которые соединяют
центроид с вершинами треугольника,
делят его на три равновеликие части.
Дано: ∆ABC
,
 — его медианы.
— его медианы.
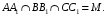
Доказать:
SAMB
=
SBMC
=
SAMC.
Доказательство.
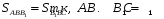 и высота, проведенная из вершины
В, у них общая.
и высота, проведенная из вершины
В, у них общая.
 т.к.
равны их основания
т.к.
равны их основания
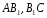 и высота, проведенная
из вершины М, у
них общая. Тогда
и высота, проведенная
из вершины М, у
них общая. Тогда

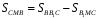 Аналогичным
образом доказывается, что
SAMB
= SAMC.
Таким образом,
SAMB
= SAMC
= SCMB
.
Аналогичным
образом доказывается, что
SAMB
= SAMC.
Таким образом,
SAMB
= SAMC
= SCMB
.
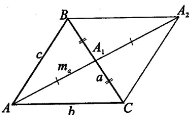 T3.
В треугольнике ABC
со сторонами а, b,
с
T3.
В треугольнике ABC
со сторонами а, b,
с
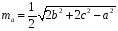 ,
где та,
тb,
тс
— медианы, приведенные соответственно
к сторонам а, b,
с треугольника.
Доказательство: 1) Обозначим
АА1
через та
и вычислим та
через a,
b
и с. 2) Продлим АА1
за точку А1
на отрезок А1А2,
равный АА1.
Тогда четырехугольник
АВА2С
— параллелограмм, так как его диагонали
АА2
и ВС
пересекаются и точкой пересечения А1
делятся пополам. Доказано, что
,
где та,
тb,
тс
— медианы, приведенные соответственно
к сторонам а, b,
с треугольника.
Доказательство: 1) Обозначим
АА1
через та
и вычислим та
через a,
b
и с. 2) Продлим АА1
за точку А1
на отрезок А1А2,
равный АА1.
Тогда четырехугольник
АВА2С
— параллелограмм, так как его диагонали
АА2
и ВС
пересекаются и точкой пересечения А1
делятся пополам. Доказано, что
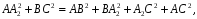 т.е.
т.е.
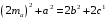 .
.
Откуда
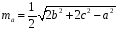 .
.
Аналогично
выводятся формулы для
 .
.
