14. Классификация точек разрыва

Существует 3 нарушения:

1. Устранимый разрыв.

Устранимым разрывом называется точка х₀, если конечный предел слева равен конечному пределу справа и  f(x₀).

2. Разрыв I рода (неустранимый).

Точкой разрыва I рода называется точка х₀, если конечные пределы (односторонние).

.

3. Разрыв II рода

Точка разрыва II рода – точка x₀, при которой хотя бы один из односторонних пределов = или не существует.

15. Замечательные пределы.

Первый замечательный предел и его следствия.

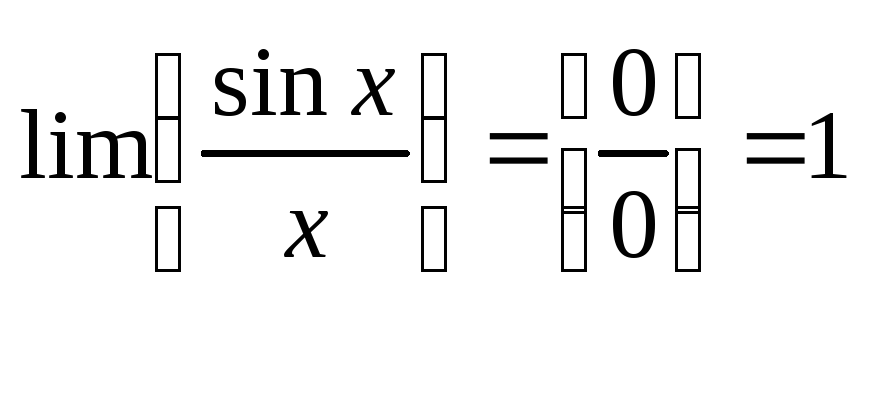- Первый замечательный предел.

Следствия:

1.

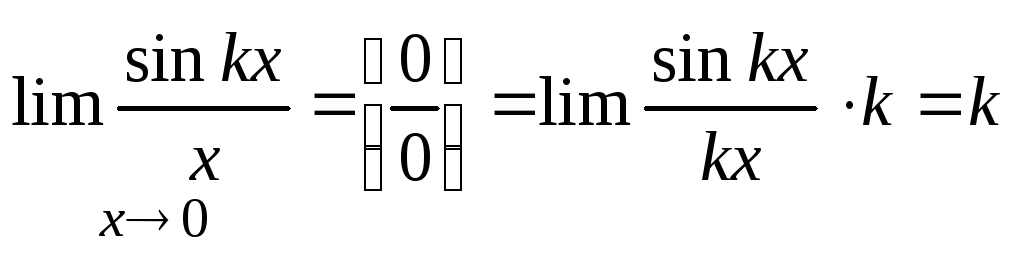
2.

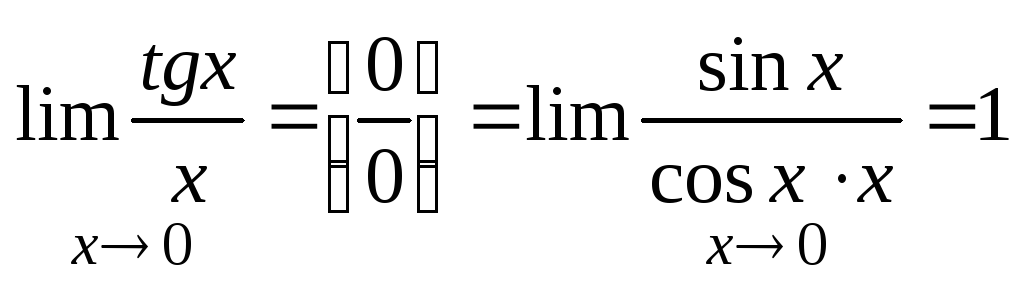
3.

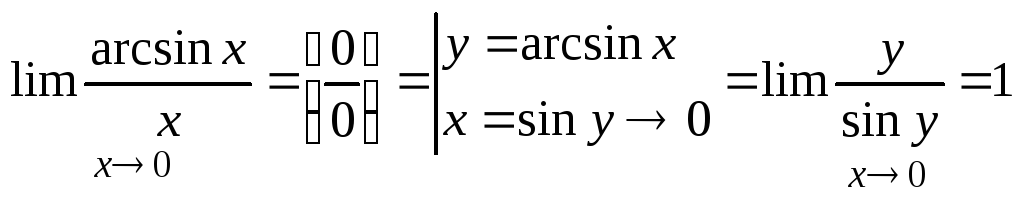
16. Второй замечательный предел и его свойства.

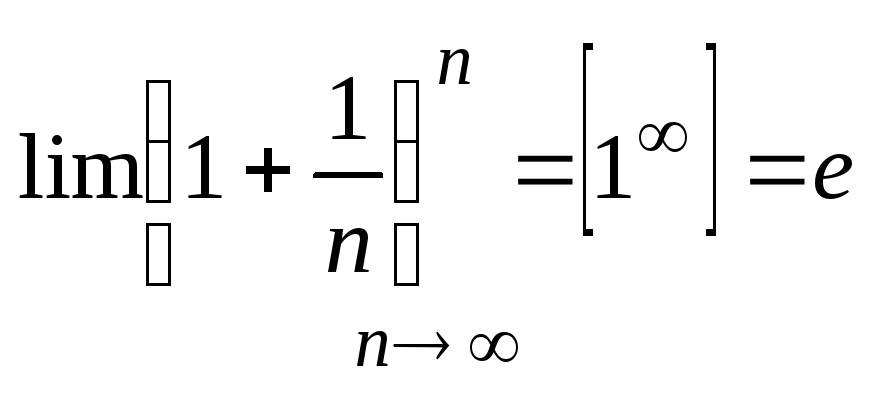- n – для натуральных чисел

- х – для любых чисел

-

Следствия:

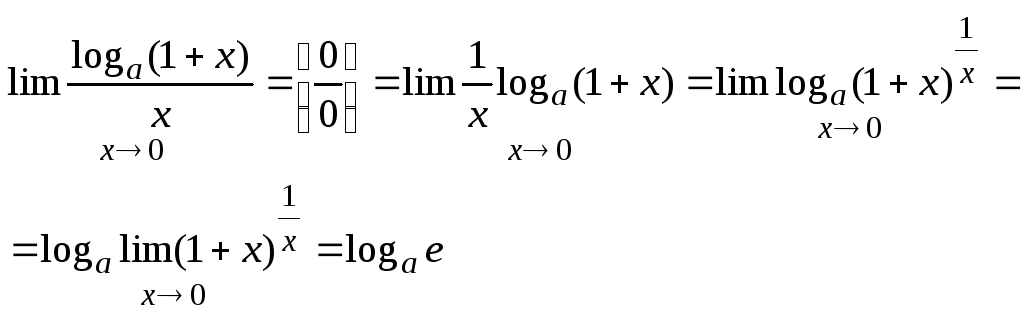1. Вывод формул:

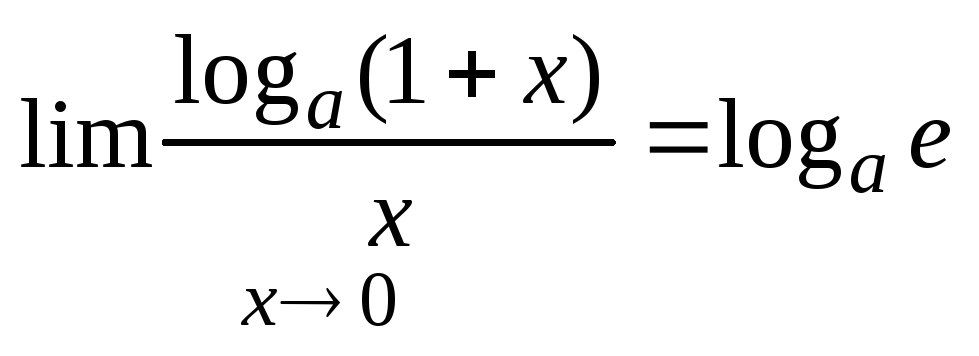
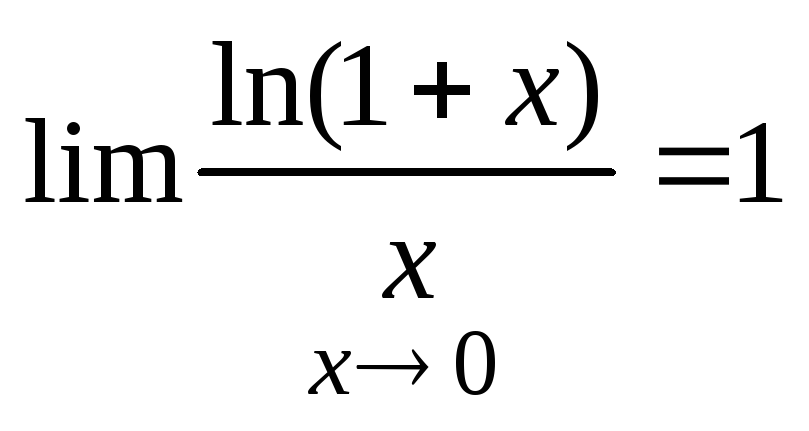
2. Вывод формулы:

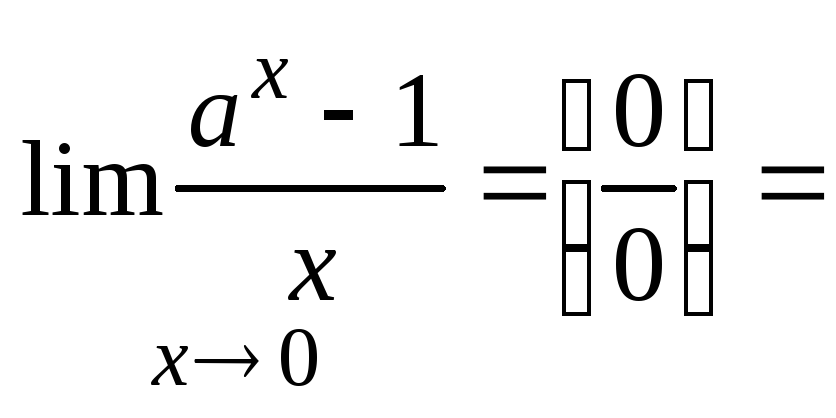
В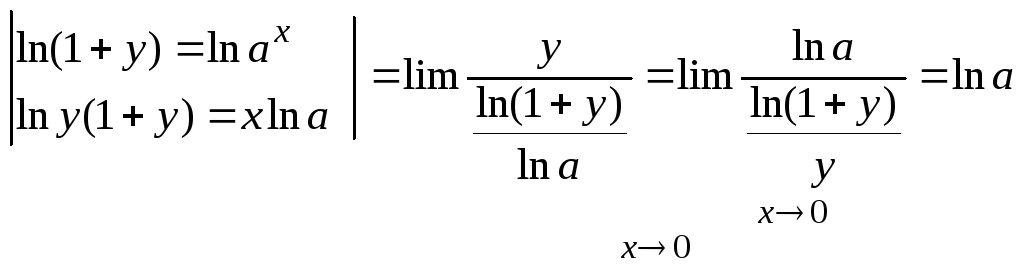водим замену:

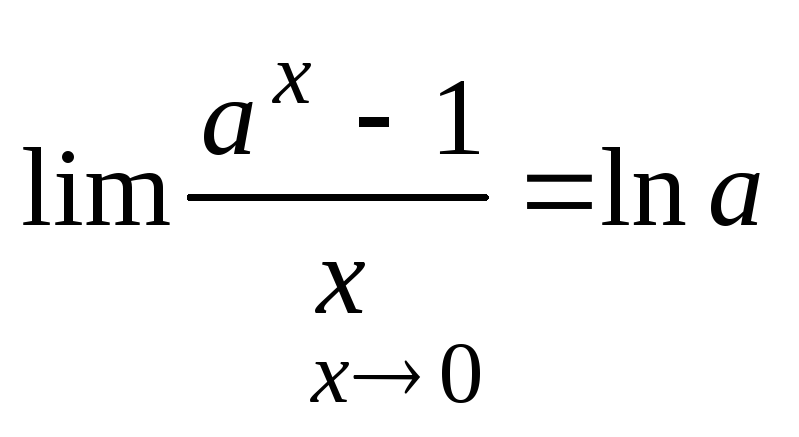
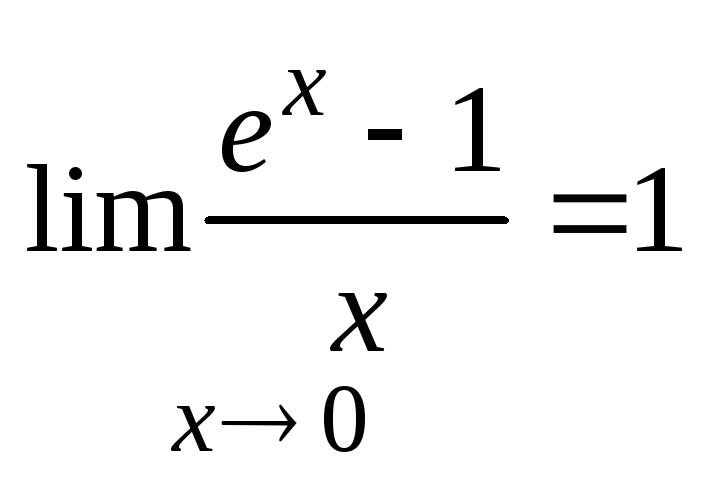
3.

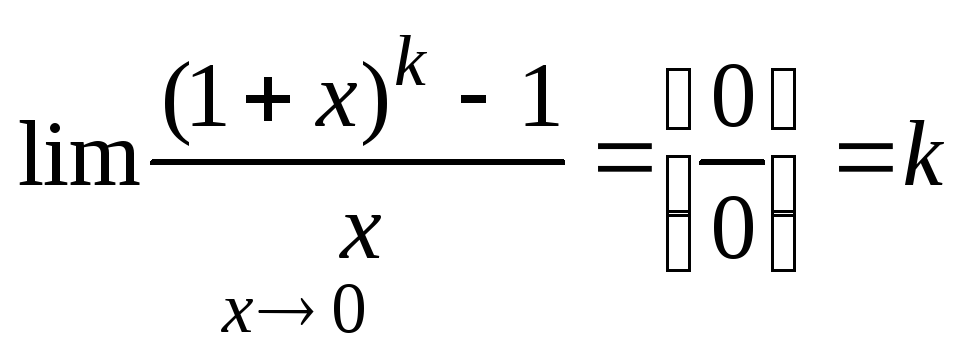
17.Бесконечно малые и бесконечно большие функции.

Функция (х) называется б.м. при хх₀, если предел этой функции равен нулю.

Функция (х) называется б.б. при хх₀, если предел этой функции равен .

Свойства б.м:

1. Сумма конечного числа б. м. функций в точке х₀ есть функция бесконечно малая в точке х₀.

2. Произведение б.м. при хх₀ на ограниченную функцию f(x) в окрестности точки х₀ есть б.м. в точке х₀.

3. Произведение конечного числа б.м. есть б.м при хх₀.

Если (х) б.м при хх0, f(x) – б.б. при хх0, то они связаны обратной зависимостью.

Если предел , то - б.м, хх₀

!Функции могут стремится к нулю с разной скоростью.

18. Главная часть б.М.

Главная часть б. м. - простейшая б.м. (х) б.м. (х).

т.е. если 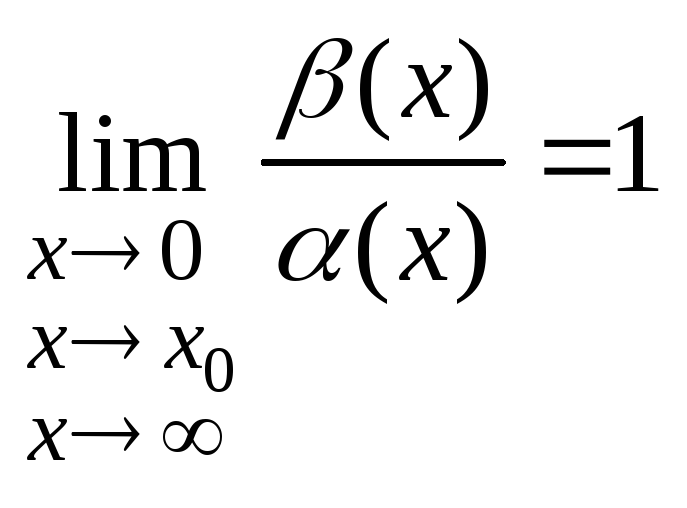, то (х) – главная часть (х)

Простейшие б.м:

При х0, (х)=сх^k

При хх₀,(х)=с(х-х₀)^k

При х,

19. Сравнение б.М.

Сравнимыми называются б.м. функции (х) и (х) при х=х₀, если существует хотя бы один из пределов

Порядком малости – называется вещественное число k (kR, k>0) (х) относительно (х), если

Чем больше порядок малости, тем скорость выше.

Правило сравнения б.м:

Пусть (х) и (х) б.м. при хх0 и пусть , тогда если:

1. С=0, тогда  имеет более порядок малости, чем , т.е. ее скорость выше: =0()

2. С=, тогда =0.

3. С0, С, тогда (=С())  и  имеют одинаковый порядок малости.

4. С=1, то  и  называют эквивалентными б.м. ().

5. С не сущ., то б.м. несравнимы.

20. Сравнение б.Б.

Функция f(x) называется б.б. при хх₀, если предел этой функции равен +,-, .

Правило сравнения б.б.

Пусть f(x) и - б.б. при хх₀ и , тогда если:

С=, то f(x) имеет более высокий порядок роста.

С=0, то имеет более высокий порядок роста.

С0, С, то порядок роста одинаковый.

С=1, то f(x) .

Если предел не сущ., то f(x) и несравнимы.

Замечания:

Если б.б. представляет собой сумму слагаемого разного порядка роста, то она эквивалентна слагаемому наивысшего порядка роста.

При вычислении пределов в произведении, частном б.б. можно заменять эквивалентными.

21. Свойства эквивалентных бесконечно малых функций.

1. Если (х)(х) при х=х₀, то и (х)(х).

2. Если (х) (х), а (х) (х), то (х) (х).

3. Бесконечно малые (х) (х) эквивалентны тогда и только тогда, когда их разность имеет более высокий порядок малости, чем каждая из них.

4. Если б.м. представляет собой сумму б.м. разного порядка малости, то она эквивалентна слагаемому НИСШЕГО порядка малости.

5. Если (х) ₁(х), (х) ₁(х) при х = х₀ и существует то и

6. Если (х)₁(х), (х)  ₁(х), то

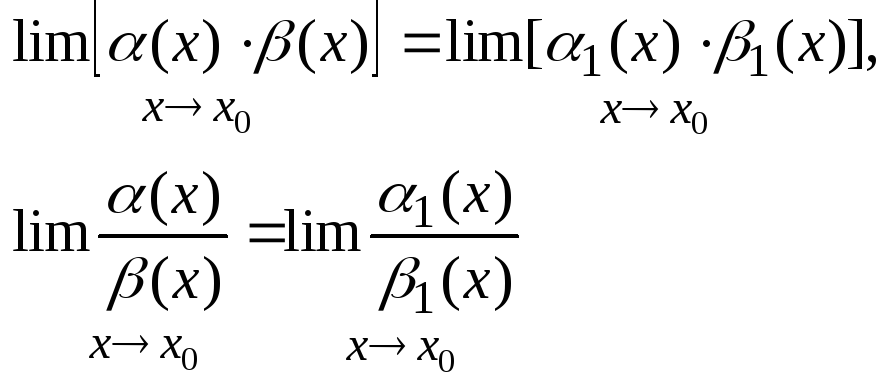
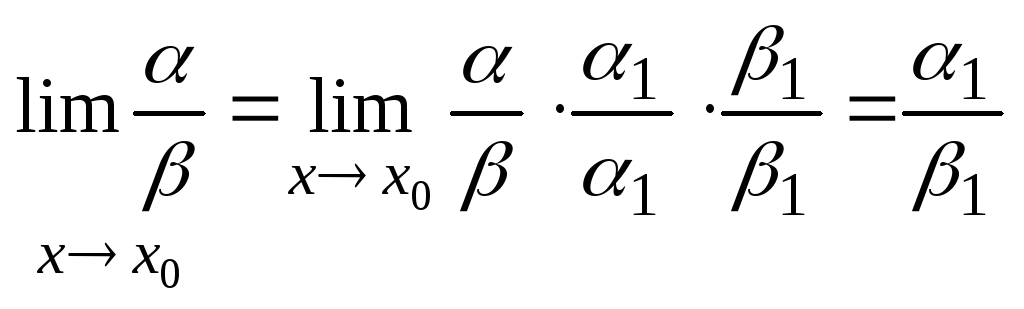
Когда функция степенная, порядок малости равен степени.