20Билет

Производная.

Производная функции у=f(x) в точке X₀ называется предел отношения приращения функции к приращению аргумента, когда последний стремится к нулю.

Задачи приводящие к понятию производная.

1. В задачах на мгновенную скорость

2. Задачи о касательной к прямой.

21Билет Правила дифференцирования

1 — постоянный множитель можно выносить за скобки.

2 — производная суммы двух функций равна сумме производных этих функций.

3 — производная произведения двух функций равна произведению производной первой функции на вторую функцию плюс произведение первой функции на производную второй функции.

#

4 — производная частного.

#

5 Производная сложной функции

Сложная функция имеет вид , где аргумент сам в свою очередь является функцией от x: . Например: .

#1.

.

#2.

.

Найдем теперь производную тангенса :

.

6 Производная обратной функции

#

Дифференциал

— эта величина равная производной функции, умноженной на приращение аргумента.

.

Второе слагаемое есть бесконечно малая величина белее высокого порядка малости в сравнении с дифференциалом. Поэтому дифференциал называют основной частью приращения функции.

Дифференциал используется в приближенных вычислениях.

# Пусть требуется вычислить синус 33 градусов. x=30=π/6, Δx=3=π3/180=0,52, =0,896

Дифференциал аргумента в точности равен его приращению:

.

Дифференциал аргумента есть число. Дифференциал функции есть функция.

Тогда дифференциал функции записывают так

, а производную как отношение дифференциалов.

Производные высших порядков.

22Билет Производная синуса



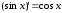
По формуле тригонометрии

.

Тогда .

Вопрос 23

Производная сложной функции, производная обратной функции.

Определение сложной функции- если на некотором промежутке Х определена функция z=ф(х) с множеством значений Z, а на множестве Z определена функция у=f(z), то функция у=f[ф(х)] называется сложной функцией от х, а переменная z промежуточной переменной сложной функции.(ф это фи)

У=f(ф), ф=ф(х)

# у= у=sinф; ф=; [ф(х)]=f'(ф)*ф'(х)

Производная постоянной функции: у=f(х)=С; у'=0; С-пост. Число

Производная степенной функции: у=; у'=n*, n-целое положит число

Производная логарифмических функций: у=(0<а≠1); у'= =

Определение обратной функции- Пусть Х и У неот множества, и пусть задана функция f, те множества пар чисел (х;у) (х; у в котором каждое число х входит в одну и только одну пару, а каждое число у, по крайней мере в одну пару. Если в каждой паре этого множества числа х и у поменять местами то получим множество пар чисел (у;х) которое называется обратной функцией ф к функции f.

У=f(х); у=у(х); х=х(у); у =; х=; у==; х=Inу

х'у=; =lim(∆у→0)== что и требовалось доказать.

()'= ф')= теорема о производной обратной фукции

25Билет .Уравнения касательной и нормали к кривой

Рассмотрим кривую, уравнение которой есть y=f(x). Возьмем на этой кривой точку M(x₀, y₀), и составим уравнение касательной к данной кривой в точке M, предполагая, что эта касательная не параллельна оси Oy.

Уравнение прямой с угловым коэффициентом в общем виде есть у=kx + b. Поскольку для касательной k= f'(x₀), то получаем уравнение y= f'(x₀)·x + b. Параметр b найдем из условия, что касательная проходит через точку M(x₀, y₀).Поэтому ее координаты должны удовлетворять уравнению касательной: y₀= f'(x₀)·x₀ + b. Отсюда b=y₀– f'(x₀)·x₀.

Таким образом, получаем уравнение касательной y= f'(x₀)·x +y₀ – f'(x₀)·x₀ или

y = f '(x0)·(x – x0) + f(x0)

Если касательная, проходящая через точку М(x₀,y₀) параллельна оси ординат (т.е. производная в этой точке не существует), то ее уравнение x= x₀.

Наряду с касательной к кривой в данной точке часто приходится рассматривать нормаль.

Нормалью к кривой в данной точке называется прямая, проходящая через эту точку перпендикулярно к касательной в данной точке.

Из определения нормали следует, что ее угловой коэффициент k_nсвязан с угловым коэффициентом касательной k равенством:

.

Учитывая, что нормаль также как и касательная проходит через точку M(x₀, y₀), то уравнение нормали к кривой y= f(x) в данной точкеM имеет вид:

Ясно, что если касательная параллельна оси Ox, т.е.f'(x₀) = 0 и ее уравнение имеет вид y= y₀, то нормаль в этой же точке будет перпендикулярна оси Ox. Значит, ее уравнение имеет вид x= x₀.

Билет 27. Дифференциал функций.

— эта величина равная производной функции, умноженной на приращение аргумента.

.

Второе слагаемое есть бесконечно малая величина белее высокого порядка малости в сравнении с дифференциалом. Поэтому дифференциал называют основной частью приращения функции.

Дифференциал используется в приближенных вычислениях.

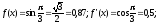
# Пусть требуется вычислить синус 33 градусов. x=30=π/6, Δx=3=π3/180=0,52, =0,896

Дифференциал аргумента в точности равен его приращению:

.

Дифференциал аргумента есть число. Дифференциал функции есть функция.

Тогда дифференциал функции записывают так

, а производную как отношение дифференциалов.

Производные высших порядков

Билет 28. Основные теоремы о производных ( Ролля, Лагранжа)

Теорема Ролля

Пусть функция определена на отрезке, причем: 1) она непрерывна на этом отрезке; 2) дифференцируема внутри отрезка, 3) значения функции на концах отрезка равны. Тогда внутри отрезка существует точка, в которой производная обращается в нуль.

Теорема Лагранжа

Пусть функция определена на отрезке, причем: 1) она непрерывна на этом отрезке; 2) дифференцируема внутри отрезка. Тогда внутри отрезка существует точка, для которой справедливо равенство

.

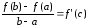 Рассмотрим вспомогательную функцию

.

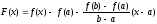Функция удовлетворяет всем трем условиям теоремы Ролля. Следовательно, внутри отрезка существует точка, для которой производная этой функции равна нулю, т. е.

.

Откуда и получаем уравнение. 

БИЛЕТ 37

Определённый интеграл — аддитивный монотонный нормированный функционал, заданный на множестве пар, первая компонента которых есть интегрируемая функция или функционал, а вторая — область в множестве задания этой функции (функционала).

Данное выше определение интеграла при всей его кажущейся общности в итоге приводит к привычному пониманию определённого интеграла, как площади подграфика функции на отрезке.

Пусть f(x) определена на [a;b]. Разобьём [a;b]на части с несколькими произвольными точками a = x₀ < x₁ < x₂ < x_n = b Тогда говорят, что произведено разбиение R отрезка [a;b] Далее выберем произв. точку , i = 0, Определённым интегралом от функции f(x) на отрезке [a;b]называется предел интегральных сумм Θ_R при , если он существует независимо от разбиения R и выбора точек ξ_i, т.е.  (1) Если существует (1), то функция f(x) называется интегрируемой на [a;b] – определение интеграла по Риману.

• 

• a – нижний предел.

• b – верхний предел.

• f(x) – подынтегральная функция.

• λ_R - длина частичного отрезка.

• σ_R – интегральная сумма от функции f(x) на [a;b] соответствующей разбиению R.

• λ_R - максимальная длина част. отрезка.

Определение интеграла на языке , δ:(по "Коши") Число I – называется определённым интегралом от f(x) на [ a ; b ], если для любого ε>0 существует δ=δ(ε)>0: для любого разбиения R отрезка [ a ; b ]: λ_R < δ, выполняется неравенство: |I- σ_R | = |∑^n-1_i=0f(ξi) Δxi - I| < ε при любом ξi є [ xi ; xi+1] Тогда I = ∫_a^bf(x)dx

[править]Геометрический смысл

Определённый интеграл как площадь фигуры

Определённый интеграл 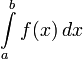 численно равен площади фигуры, ограниченной осью абсцисс, прямыми x = a и x = b и графиком функции f(x).

Определенный интеграл

3.4.2. Свойства определенного интеграла

Доопределим понятие интеграла при a ≥ b следующими равенствами:

Сформулируем некоторые свойства определенного интеграла в предположении, что подынтегральная функция ограничена на отрезке, по которому она интегрируется.

• Если функция интегрируема на [a; b], то она интегрируема на любом отрезке 

• Для любых a, b и c

• Интеграл обладает свойством линейности: для любых функций f (x) и g (x) и любой постоянной A

• Если f (x) и g (x) интегрируемы на [a; b], то f (x) · g (x) также интегрируема на этом отрезке.

• Если f (x) – периодическая функция с периодом T, то для любого a

Модель 3.10. Свойства определенного интеграла

Для определенных интегралов верны также следующие оценки (предполагается, что функции f и g интегрируемы на [a; b]).

• Если f (x) ≥ g (x), то 

• В частности, если f (x) ≥ 0, то 

• Если f (x) ≥ 0 для любого  и существует  такое, что  причем f (x) непрерывна в  то 

• |f (x)| интегрируема на [a; b], причем 

• Если на отрезке [a; b]  m ≤ f (x) ≤ M, то 

Рисунок 3.4.2.1. Численное вычисление определенного интеграла при помощи формулы трапеций

БИЛЕТ 38

Замена переменной в определенном интеграле

Для определенного интеграла справедливы все типы замен, что и для неопределенного интеграла. Таким образом, если с заменами у Вас не очень, следует внимательно ознакомиться с уроком Метод замены в неопределенном интеграле.

В этом параграфе нет ничего страшного или сложного. Единственная новизна состоит в вопросе, как поменять пределы интегрирования при замене.

В примерах я постараюсь привести такие типы замен, которые еще нигде не встречались на сайте.

Пример 5

Вычислить определенный интеграл

Главный вопрос здесь вовсе не в определенном интеграле, а в том, как правильно провести замену. Смотрим в таблицу интегралов и прикидываем, на что у нас больше всего похожа подынтегральная функция? Очевидно, что на длинный логарифм:  . Но есть одна неувязочка, в табличном интеграле под корнем , а в нашем – «икс» в четвёртой степени. Из рассуждений следует и идея замены – неплохо бы нашу четвертую степень как-нибудь превратить в квадрат. Это реально.

Сначала готовим наш интеграл к замене:

Из вышеуказанных соображений совершенно естественно напрашивается замена:  Таким образом, в знаменателе будет всё хорошо: . Выясняем, во что превратится оставшаяся часть  подынтегрального выражения, для этого находим дифференциал :

 

По сравнению с заменой в неопределенном интеграле у нас добавляется дополнительный этап.

Находим новые переделы интегрирования.

Это достаточно просто. Смотрим на нашу замену  и старые пределы интегрирования , .

Сначала подставляем в выражение замены  нижний предел интегрирования, то есть, ноль:

Потом подставляем в выражение замены  верхний предел интегрирования, то есть, корень из трёх:

Готово. И всего-то лишь…

Продолжаем решение.

(1) В соответствии с заменой записываем новый интеграл с новыми пределами интегрирования.

(2) Это простейший табличный интеграл, интегрируем по таблице. Константу  лучше оставить за скобками (можно этого и не делать), чтобы она не мешалась в дальнейших вычислениях. Справа отчеркиваем линию с указанием новых пределов интегрирования  – это подготовка для применения формулы Ньютона-Лейбница.

(3) Используем формулу Ньютона-Лейбница .

Ответ стремимся записать в максимально компактном виде, здесь я использовал свойства логарифмов.

Ещё одно отличие от неопределенного интеграла состоит в том, что, после того, как мы провели замену, никаких обратных замен проводить не надо.

40) Дифференциальное уравнение с разделяющимися переменными

.

Решение. Выполним преобразование:

.

(обе части уравнения разделили на N(y) и умножили на dx)

Получили уравнение с разделенными переменными, поэтому найдем общее решение интегрированием левой и правой частей.

Билет №41 Линейные дифференциальные уравнения первого порядка

Обыкновенное дифференциальное уравнение вида

называется линейным дифференциальными уравнениями. Для его решения обычно используют метод вариации постоянной. Для этого сначала необходимо решить соответствующее однородное дифференциальное уравнение

которое является дифференциальным уравнением с разделяющимися переменными. Полученное общее решение этого уравнения надо подставить в исходное обыкновенное дифференциальное уравнение, неоднородное дифференциальное уравнение, считая, что . Затем необходимо решить полученное обыкновенное дифференциальное уравнение относительно неизвестной функции и подставить его решение в ранее полученную формулу .

Чтобы решить уравнение Бернулли вида

необходимо сделать замену переменной . После замены будет получено линейное дифференциальное уравнение.

Билет №42

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентов.

1)у¹¹+ру¹+qy=f(x)

Если f(x)=0 то это дифференциальные уравнения 2 порядка с постоянным коэффициентом.

2)y¹¹+py¹+qy=0

Пусть у нас переменная у¹ и у² являются частным решениями данного диф., урав., тогда ( проверьте по своим записям!!!!!) f(y_i;y₁) также явл., решением данного уравнения.

Дан пример:

У₁¹¹+у₂¹¹+р(у₁¹+у₂¹)+q(y₁+y₂)=0

(y₁¹¹+py₁¹+py₂¹)+(y₂¹¹+qy₁+qy₂)=0

0 0

Если является у₁ решением, то величина (у¹ явл решением(конец проверьте!!!!)

Стоит квадратик сy₁¹¹+pcy₁¹+qcy=0

(y₁¹¹+py¹₁+qy₁)=0 стоит квадратик

43билетСлучайные события

Определение, основные формулы  Классическое определение вероятности 

(m - число благоприятных исходов опыта; n - число всех его исходов)

     Теорема сложения вероятностей несовместных событий 

     Теорема сложения вероятностей совместных событий 

     Теорема умножения вероятностей независимых событий 

     Теорема умножения вероятностей зависимых событий 

где  - вероятность события B при условии, что произошло событие A.

     Формула полной вероятности 

где  - полная группа гипотез, т. е.

( - достоверное событие).

  Формула Бейеса 

где  - полная группа гипотез.

     Повторение испытаний       Формула Бернулли 

где  - вероятность появления события A ровно k раз при n независимых испытаниях; p - вероятность появления события A при каждом испытании.

     Вероятность того, что при этом событие A:

     1) наступит n раз: ;

     2) не наступит ни разу: ;

     3) наступит хотя бы один раз: ;

     4) наступит не более k раз: ;

     5) наступит не менее k раз: .

     Локальная теорема Лапласа 

где  - вероятность появления события A ровно k раз при n независимых испытаниях; p - вероятность появления события A при каждом испытании; .

Интегральная теорема Лапласа 

где  - вероятность того, что в n независимых испытаниях событие A появится не менее k₁ и не более k₂ раз;  - функция Лапласа; ; .

     Оценка отклонения относительной частоты от постоянной вероятности 

     Наивероятнейшее число k₀ появления события A при n независимых испытаниях

(n - число испытаний; p - вероятность появления события при одном испытании).

Статическое определение вероятностей

 

Классическое определение не требует проведения опыта. В то время как реальные прикладные задачи имеют бесконечное число исходов, и классическое определение в этом случае не может дать ответа. Поэтому в таких задачах будем использовать статическое определение вероятностей, которое подсчитывают после проведения эксперимента или опыта.

 

Статической вероятностью w(A) или относительной частотой называют отношение числа благоприятных данному событию исходов к общему числу фактически проведенных испытаний.

w(A)=nm

 

Относительная частота события обладает свойством устойчивости:

limn→∞P(∣ ∣  nm−p∣ ∣  <ε)=1 (свойство устойчивости относительной частоты)